Глава IV

4.1. Любая примитивно рекурсивная функция получается из простейших функций с помощью конечного числа применения операций суперпозиции и примитивной рекурсии. Но простейшие функции ивсюду определены, а применение к ним операции суперпозиции и схемы примитивной рекурсии приводит к функциям, которые всюду определены.

4.2. Функция ,,иполучаются из функцийи

(m=1, 2, ..., n) суперпозициями:

1) ;

2) =;

3) =;

4) =.

4.3. Пусть получена из функции О(х) и с помощью суперпозиции и схем примитивной рекурсии. Тогдаf(0,…,0)= 0, и из условия следует, что . Функциих+1 и 2х этим двум условиям одновременно не удовлетворяют.

4.4. 1) Функция Р(х,у)=ху может быть получена из простейших функций с помощью схемы примитивной рекурсии. Действительно, т.к. для функции Р(х,у) верны тождества

Р(0,х)=х0=0=О(х),

Р(у+1,х)=х(у+1)=ху+х=х+Р(х,у)=S(х,Р(х,у)),

то функции Р(х,у) получается по схеме примитивной рекурсии из функций О(х) и S(х,у)=х+у , которые являются общерекурсивными и, значит, функция Р(х,у) общерекурсивна.

2) Функция G(x,y)=x^y удовлетворяет соотношениям:

или

Следовательно, функцияG(х,у) может быть получена по схеме примитивной рекурсии из общерекурсивных функций С₁ и Р и поэтому является общерекурсивной.

3) Функция х-1, если х > 0 удовлетворяет

0, если x = 0

соотношениям: или.

Значит, функция получается по схеме примитивной рекурсии из общерекурсивных функций и поэтому сама является общерекурсивной.

4) Чтобы доказать, что усеченная разность является общерекурсивной функцией, докажем предварительно, что общерекурсивной функцией является функция одной переменной х-1, которая получается из усеченной разности путем фиксирования второго аргумента. Действительно, функция х-1 удовлетворяет следующим соотношениям:

и, значит, может быть получена из простейших функций по схеме простейшей рекурсии и поэтому является общерекурсивной.

Теперь ясно, что функция х-у при любых х и у удовлетворяют равенствам:

Эти тождества показывают, что усеченная разность может быть получена из функций ипо схеме примитивной рекурсии и, значит, является общерекурсивной.

5) Функция |x-y| может быть представлена в виде:

|x-y|=(х-у)+(у-х)=S(x-y,y-x),

т.е. функция |x-y| получается из общерекурсивных функций S, x-y, y-x с помощью операции суперпозиции и, следовательно, является общерекурсивной.

6) Функцию sgn(x) можно определить с помощью простейшей рекурсии, используя равенства:

или .

0, если

7) Функция (х)= 1, если и, следовательно, (х)=1-(х).Таким образом, функция (х)получается с помощью операции суперпозиции из функций sgn(x), каждая из которых общерекурсивна и поэтому функция (х) общерекурсивна.

8) Функция х! удовлетворяет равенствам

или

т.е. функция х! может быть получена по схеме примитивной рекурсии из общерекурсивных функций ии поэтому функциях! общерекурсивна.

4.5. Программа реализации на машине Тьюринга алгоритма вычисления функции имеет вид:

		0	1	2	3	4	5	6	7	8	9
		4	5	6	7	8	9	0	1	2	3
		1	2	3	4	5	6	7	8	9	0

4.6. Программа реализации на машине Тьюринга алгоритма вычисления функции имеет вид:

		|
		|

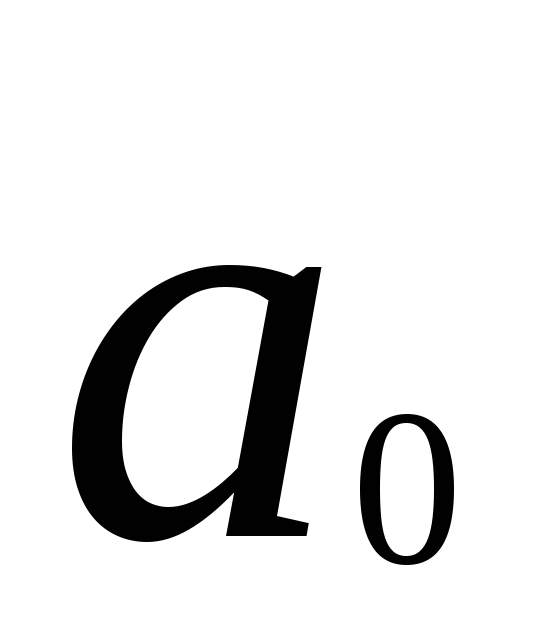
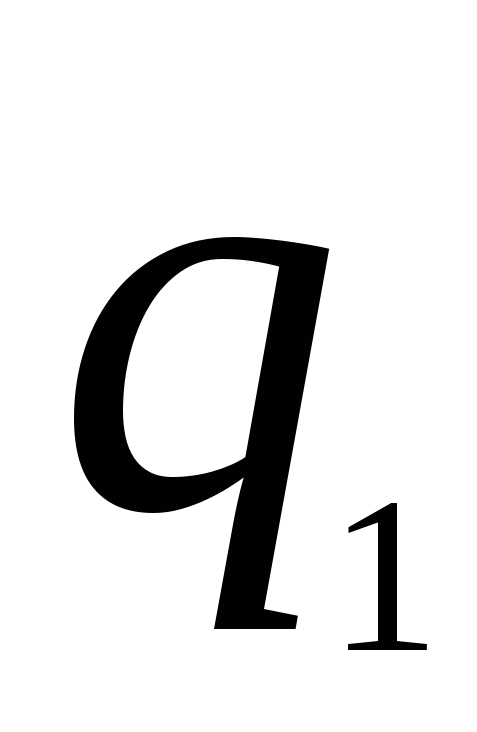
Здесь внешний алфавит машины – есть множество символов , а начальная конфигурация может быть любой, при которой управляющая головка обозревает клетку, содержащую палочку.

4.7. Внешний алфавит машины, очевидно, состоит из двух символов . Пусть при начальной конфигурации запись на ленте воспринимается машиной в стандартном положении. Своевременной остановки машины после каждого такта. Это и учтено программой машины, внутренний алфавит которой содержит три состояния - , ,.

		|
		|
		|

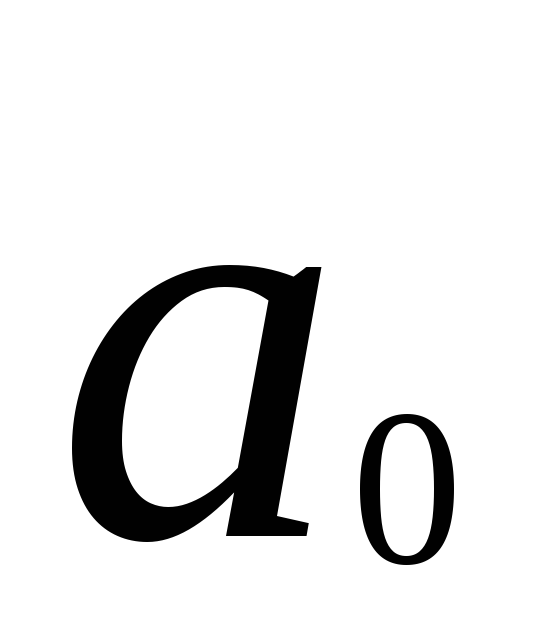
4.8. Очевидно, для решения задачи машине в начальном состоянии при конфигурации

…

необходимо заменить букву на и, двигаясь вправо до первой пустой клетки, вписать в нее букву . Т.к. в алфавите всего две буквы и, то для правильного решения задачи необходимо еще два состояния: вписывает букву , если =, вписывает букву , если =. Поэтому программа машины имеет вид:

4.9. Ясно, что в начальной конфигурации управляющая головка машины должна обозревать пустую клетку, первую от слова х справа, если , и любую, еслих = 0:

|

|

|

|

В первом такте работы машины необходим сдвиг ее влево и переход в новое состояние . Если и здесь обозревается пустая клетка, то х = 0, и машине необходим сдвиг вправо и переход в стоп-состояние. Если в состоянии

, управляющая головка обозревает символ |, то , и палочку следует оставить, переходя влево в новом состоянии . Если при этом обозревается пустая клетка, то процесс вычисления закончен, и нужно перейти вправо в стоп-состояние. Если же в состоянии обозревается вновь символ |, то его нужно стереть и перейти влево в том же состоянии . В этом состоянии машина должна работать до тех пор, пока управляющая головка не выйдет на пустую клетку. На этом процесс вычисления заканчивается и необходимо для оформления результата перейти в состояние , которое будет совершать сдвиги машины до единственного оставшегося символа |, на котором и следует перейти в стоп-состояние. Т.о., программа машины имеет вид:

		|
		|
		|

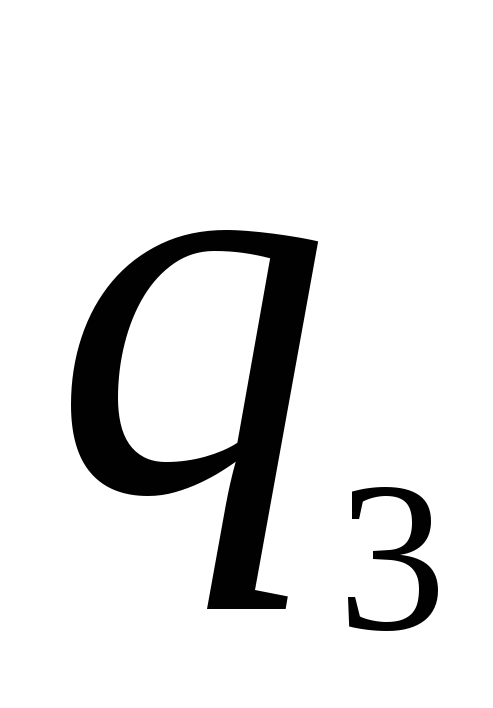
4.10. нетрудно видеть, что, проводя рассуждения как в задаче 4.9., можно ограничиться тремя активными состояниями , , и получить программу машины в виде:

		|
	|
		|

4.12. Для решения поставленной задачи работу машины Тьюринга можно представить следующим образом: во внешний алфавит машины включены четыре буквы: . Символ | (палочка) обозначает единицу, аииграют роль временных палочек. Число записано на ленте в виде набораn палочек. Это слово воспринимается машиной в стандартном положении. Например,

| | | | .

В первом такте работы машины осуществляется сдвиг вправо, и машина остается в состоянии . При этом машина вписывает в пустую клетку букву , сдвигается влево и переходит в состояние . В состоянии машина в каждом такте сдвигается влево, оставляя без изменений буквы и. При достижении буквы | в состоянии буква | заменяется на , осуществляется сдвиг влево и переход в состояние . Если при этом управляющая головка обозревает пустую клетку, то машина переходит в состояние . Если же управляющая головка в состоянии машины обозревает букву |, то, оставаясь на месте, машина переходит в состояние . В состоянии машина движется вправо до первой пустой клетки, оставляя при этом на месте буквы |, ,. Достигнув пустой клетки в состоянии машина вписывает в нее букву и далее процесс повторяется. Машина будет работать до тех пор, пока все палочки не будут заменены на буквы(столько же буквбудет вписано в пустые клетки).

При этом машина перейдет в состояние . В состоянии машина двигается вправо, заменяя буквы ина палочки. Достигнув пустой клетки в состоянии машина переходит в стоп0состояние. Следовательно, программа машины имеет вид:

		|
		|
		|
			|	|

4.13. Будем записывать число n на ленте в виде набора n палочек. Работу машины Тьюринга можно представить следующим образом. Пусть начальная конфигурация совпадает со стандартным положением машины. Тогда машина начинает двигаться влево, меняя состояния на , на и т.д., на , а на . Тогда возможны два случая:

1) машина увидит пустую клетку в состоянии (это значит, что число непустых клеток было кратно р). Тогда машина переходит в состояние и далее «стирает» все «палочки», ставит одну палочку и переходит в стоп-состояние.

2) машина увидит пустую клетку в состоянии ( это значит, что число непустых клеток не было кратнор). Тогда машина переходит в состояние и далее «стирает» все «палочки» и останавливается.

В связи со сказанным программа машины запишется так:

		|
		|
		|
…	…	…
		|
		|
	|

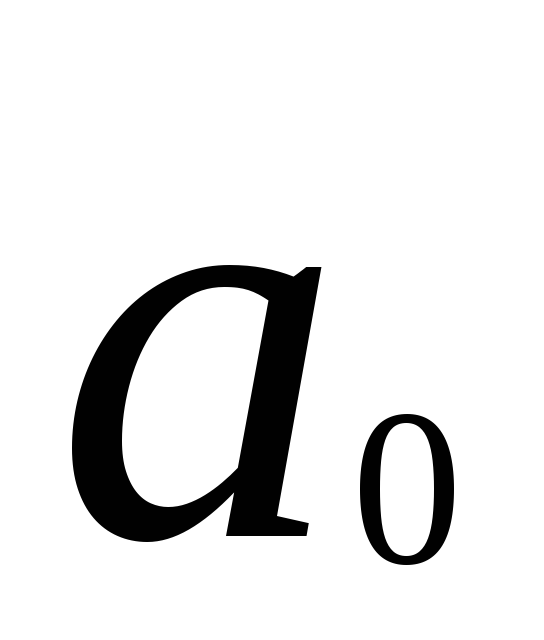
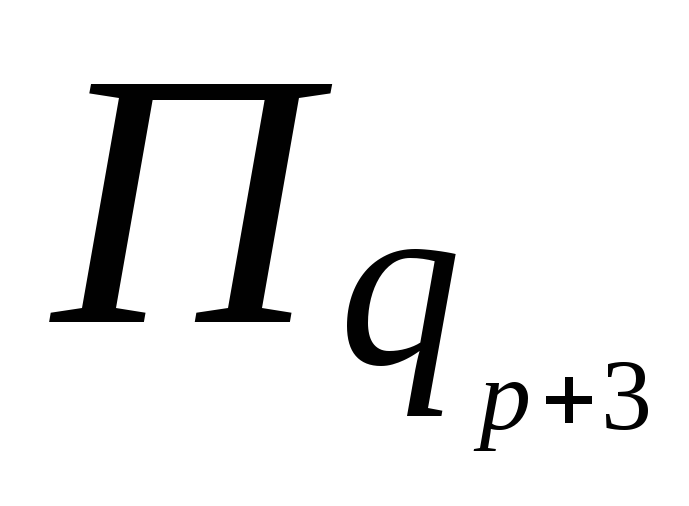
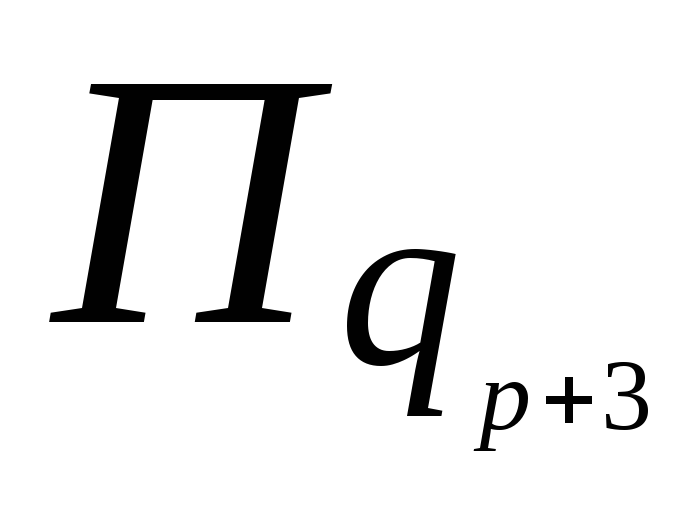
В частном случае при р = 3 эта программа будет иметь вид:

		|
	|	|
		|
		|
	|
		|
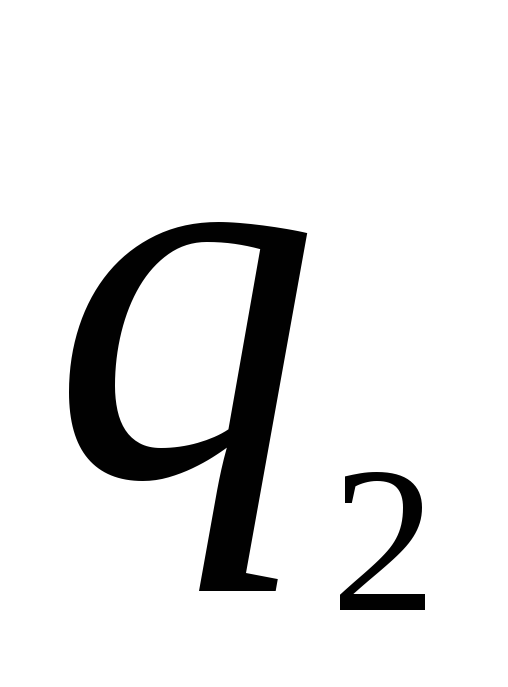