vse_laby_po_fizike / Лаб.мех / Лаб.раб.№1-колеб

11

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра физики

ИЗУЧЕНИЕ ЗАКОНОВ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОГО МАЯТНИКА

Методические указания к лабораторной работе №1 по механике

Ростов-на-Дону 2009

Составители: В.С. Ковалёва, О.А. Лещёва, О.М. Холодова.

УДК 530.1

ИЗУЧЕНИЕ ЗАКОНОВ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОГО МАЯТНИКА: Метод. указания. -Ростов н/Д:

Издательский центр ДГТУ, 2009. - 11 с.

Указания содержат краткое описание рабочей установки и методики определения ускорения свободного падения с помощью математического маятника.

Методические указания предназначены для студентов инженерных специальностей всех форм обучения при выполнении лабораторных работ по физике (раздел «Механика и молекулярная физика»).

Печатается по решению методической комиссии факультета «Нанотехнологии и композиционные материалы»

Научный редактор проф., д.т.н. В.С.Кунаков

© Издательский центр ДГТУ, 2009

Лабораторная работа №1

ИЗУЧЕНИЕ ЗАКОНОВ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОГО МАЯТНИКА

Цель работы:

Изучить колебательный процесс на примере математического маятника. Определить ускорение свободного падения.

Оборудование: экспериментальная установка.

1. Теоретическая часть.

Математическим маятник – материаль-ная точка, подвешенная на невесомой нерастя-жимой нити и совер-шающая колебания в вертикальной плоскос-ти под действием силы тяжести. Хорошим примером математи-ческого маятника слу-жит небольшой тяже-лый шарик, подве-шенный на длинной легкой нити.

При отклонении маят-ника от положения рав-новесия на угол воз-никает вращательный момент М: (1),

где m – масса маятника, g - ускорение свободного падение, l - длина нити.

Знак “-” означает, что вращательный момент имеет такое направление, что стремится вернуть маятник в положение равновесия.

Напишем для маятника уравнение динамики вращательного движения с учетом (1):

(2)

где -угловое ускорение маятника.

и приведем уравнение (2) к виду:

(3)

Будем рассматривать малые колебания при условии . Пусть (4),

Тогда уравнение (3) принимает вид: (5)

Решением уравнения (5) будет: (6)

где А - амплитуда колебаний, - фаза колебания, - циклическая частота колебаний, - начальная фаза колебаний.

Из уравнения (6) следует, что при малых углах отклонения математический маятник совершает гармонические колебания.

Период колебаний и циклическая частота связаны между собой соотношением: , учитывая (4), получим: (7)

В работе определяем ускорение свободного падения из формулы (7). Для увеличения точности нахождения “g” следует измерять время достаточно большого числа полных колебаний маятника и на разных длинах нити при малых углах отклонения. Согласно (7)

,

или (8), (9).

Вычтем из выражения (8) выражение (9):

, откуда

(10)

Периоды колебаний находятся по формулам:

, (11)

где n – число полных колебаний,

и - время колебаний первого и второго маятников соответственно.

Подставляя (11) в (10), получаем формулу для определения ускорения свободного падения:

(12)

Относительная погрешность измерения ускорения свободного падения определяется по формуле:

(13)

, где - приборная погрешность.

Доверительный интервал определения ускорения свободного падения: .

2. Порядок выполнения работы.

Задание . Определение ускорения свободного падения при помощи математического маятника.

1. Основание (1) установки отрегулировать так, чтобы положение стойки (2) было строго вертикально.

2. Установить по шкале, нанесенной на стойке (2), длину 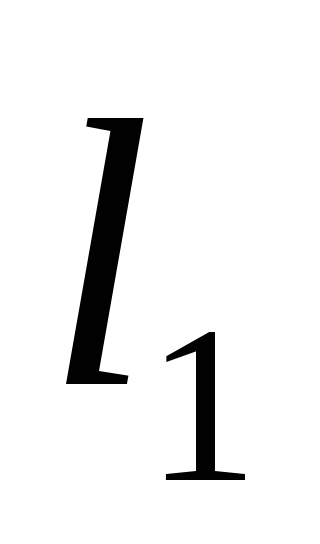математического маятника (3) и занести результат в таблицу 1.

3. Установить “ноль” в окошке секундомера (4) при помощи кнопки “сброс” (5).

4. Отвести рукой маятник в крайнее положение на небольшой угол (≈10˚). Отпустить маятник и нажать кнопку “пуск” (5).

5. Измерить время t₁ для n=10-20 полных колебаний (по указанию преподавателя). В окошке (4) идет счет полным колебаниям. Кнопку “стоп” (5) следует нажать в тот момент, когда в окошке (4) высветится предпоследнее по счету колебание.

6. Пункт 5 повторить 3-5 раз (по указанию преподавателя). Результаты занести в таблицу 1.

7. Повторить пункты 2- 6 для маятника длиной l₂ меньшей, чем l₁. Все измерения занести в таблицу 1.

8. По формуле (12) найти g по средним значениям t₁ и t₂.

9. Провести статистическую обработку измерений времени, заполнив таблицы 2 и 3.

10. По формуле (13) определить относительную погрешность определения ускорения свободного падения.

Таблица1.

№ n/n	n		t1			t2	g	Δg	εg
		м	с	м	м	с	м/с2	м/с2	%
1 2 3 4 5
Ср.зн.

Таблица2.

№ n/n	t1	Δt1	(Δt1)2	Sn,t	tn,α	Δt1сл	Δt1пр	Δt1дов	ε1
	c	c		c		c	c	c	%
1 2 3 4 5
Ср.зн.

Таблица3.

№ n/n	t2	Δt2	(Δt2)2	Sn,t	tn,α	Δt2сл	Δt2пр	Δt2дов	ε1
	c	c		c		c	c	c	%
1 2 3 4 5
Ср.зн.

Контрольные вопросы

1. Что такое колебания? Собственные колебания? Свободные колебания? Гармонические колебания?

2. Дайте определения амплитуды, фазы, периода, частоты, циклической частоты колебания?

3. Что называется математическим маятником?

4. Какие колебания математического маятника считаются малыми?

5. Выведите формулу периода колебаний математического маятника.

6. Как можно определить период колебаний маятника экспериментально?

7. Запишите уравнение гармонического колебания, поясните физический смысл всех входящих в него величин.

8. Получите формулу для расчета максимальной скорости колеблющейся точки.

9. Получите формулу для расчета максимального ускорения колеблющейся точки.

10. Получите формулу для определения восстанавливающей силы и её максимальное значение.

11. Получите дифференциальное уравнение гармонических колебаний.

12. Сделайте вывод формулы погрешности (13).

13. Почему колебания математического маятника иногда называют квазиупругими колебаниями?

Рекомендуемая литература

1. Савельев И.В. Курс общей физики (т.1). М.: Наука, СПб.: Лань, 2006.

2. Трофимова Т.И. Курс физики. М.: Высш. Шк., 2004.

3. Справочное руководство по физике. Ч.1. Механика, молекулярная физика, электричество, магнетизм: Учеб.-метод. пособие.-Ростов н/Д: Издательский центр ДГТУ, 2009.

4. Федосеев В.Б. Физика. Ростов н/Д: Феникс, 2009.

Техника безопасности

1. К работе с установкой допускаются лица, ознакомленные с её устройством и принципом действия.

2. Для предотвращения опрокидывания установки необходимо располагать её только на горизонтальной поверхности.

Составители: В.С. Ковалёва, О.А. Лещёва, О.М. Холодова.

ИЗУЧЕНИЕ ЗАКОНОВ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОГО МАЯТНИКА.

Методические указания к лабораторной работе по физике

Редактор А.А.Литвинова

В печать

Объём 0,7 усл.п.л. Офсет. Формат 60х84/16.

Бумага тип №3. Заказ № . Тираж . Цена

Издательский центр ДГТУ

Адрес университета и полиграфического предприятия:

344010, г.Ростов-на-Дону, пл.Гагарина,1.