ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра физики

Изучение законов колебательного движения с помощью физического маятника

Методические указания к лабораторной работе №2

(Раздел «Механика»)

Ростов-на-Дону 2010

Составители: В.С. Ковалёва, О.А. Лещёва, О.М. Холодова.

УДК 530.1

ИЗУЧЕНИЕ ЗАКОНОВ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ ФИЗИЧЕСКОГО МАЯТНИКА: Метод. указания. -Ростов н/Д:

Издательский центр ДГТУ, 2010. - 12 с.

Указания содержат краткое описание рабочей установки и методики определения момента инерции физического маятника.

Методические указания предназначены для студентов инженерных специальностей всех форм обучения при выполнении лабораторных работ по физике (раздел «Механика и молекулярная физика»).

Печатается по решению методической комиссии факультета «Нанотехнологии и композиционные материалы»

Научный редактор проф., д.т.н. В.С.Кунаков

© Издательский центр ДГТУ, 2010

Лабораторная работа №2 изучение законов колебательного движения с помощью физического маятника

Цель работы:

Изучить колебательный процесс на примере физического маятника. Определить приведенную длину и моменты инерции физического маятника.

Оборудование: экспериментальная установка.

1. Теоретическая часть.

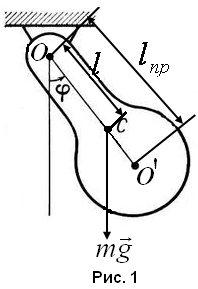Физический маятник - твердое тело, которое может совершать колебания под действием силы тяжести относительно неподвижной горизонтально расположенной оси, не проходящей через центр масс тела (рис.1). Такая ось называется осью колебания, точка – точкой подвеса маятника. Плоскость, проходящая через точки и перпендикулярно оси колебания, называется плоскостью колебания. В положении равновесия центр масс маятника находится под точкой подвеса маятника , на одной вертикали.

При отклонении маятника от положения равновесия на угол возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен:

, (1)

где - расстояние между точкой подвеса и центром масс маятника, – масса физического маятника.

Знак “ - ” означает, что вращательный момент имеет такое направление, что стремится вернуть маятник в положение равновесия.

На основании основного уравнения динамики вращательного движения можно написать:

, (2)

где – момент инерции маятника относительно оси, проходящей через точку подвеса, - угловое ускорение маятника.

В случае малых колебаний (), уравнение (2) можно записать:

(3)

где (4)

Из уравнения (3) следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания. Период колебаний можно определить из (4):

(5)

где (6) называется приведенной длиной физического маятника.

Приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

Центр качания - это точка на прямой, соединяющей точку подвеса с центром масс, лежащая на расстоянии приведенной длины от оси колебания (точка на рис.1).

По теореме Штейнера момент инерции маятника равен:

, (7)

где - момент инерции относительно оси, параллельной оси колебания и проходящей через центр масс маятника, - расстояние от оси вращения до центра масс.

Решая (6) и (7), получим . (8)

И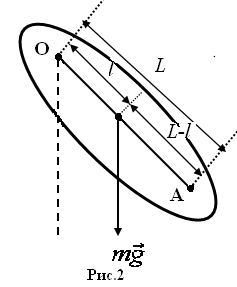з (8) видно, что всегда больше , так что точка подвеса и центр качания лежат по разные стороны от центра масс.

Для определения поступим следующим образом. Подвесим физический маятник в точке . Момент инерции относительно точки , с учетом формулы (5), равен:

, (9)

где - период колебаний относительно точки .

Если маятник перевернуть, то момент инерции относительно точки равен:

, (10)

где - период колебаний относительно точки подвеса .

Воспользовавшись формулой (7), имеем:

(11)

(12)

Вычтем из (12) формулу (11) и получим:

(13)

Вычтем из (10) выражение (9) и получим

(14)

Решая (13) и (14), имеем

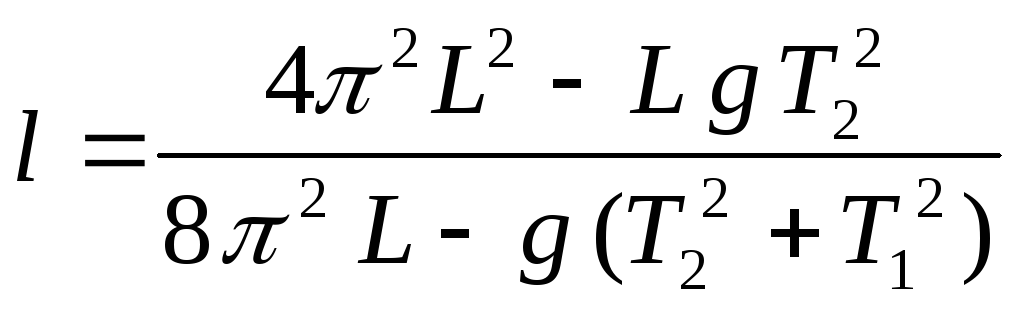(15)

Поскольку периоды колебаний находятся как

и , получаем рабочую формулу:

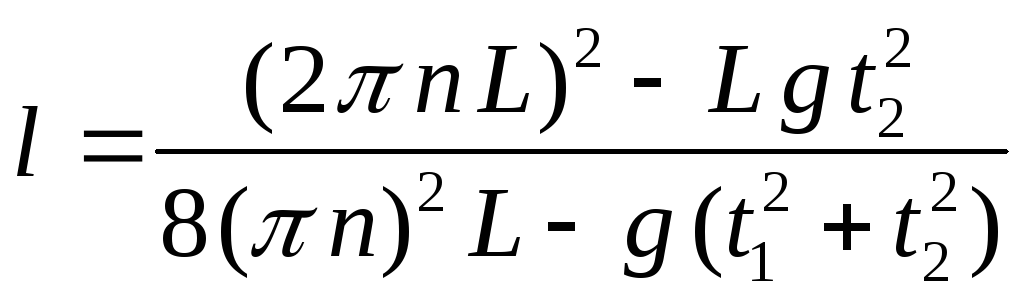. (16)

В работе моменты инерции маятника определяются по формулам (9) и (10) с учетом (16).