дгту / королькова / Математика к.р.2

Контрольная работа №2

Вариант 6.

Задание 1. Найти производные первого порядка данных функций:

а)

б)

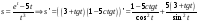
в)

г)

Задание 2. Составить уравнение касательной и нормали к кривой у=f(x) в точке с абсциссой х₀:

Уравнение касательной в точке с абсциссой х₀ имеет вид:

_{Тогда при х0} = 2:

_{Определим уравнение касательной в точке х0:}

Нормаль - прямая, проходящая через точку касания перпендикулярно касательной. поэтому ее угловой коэффициент равен , а уравнение записывается в виде: .

_{Определим уравнение нормали в точке х0:}

Задание 3. Найти производную функции у = у(х), заданной параметрически: .

Решение:

,

,тогда

Задание 4. Найти дифференциалы функций:

а)

б)

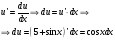
в)

Задание 5. Найти производную второго порядка функции у = f(x):

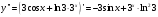
Задание 6. Вычислить скорость и ускорение движения при прямолинейном движении точки в момент времени t = t₀, если S = s(t) – закон движения, S –путь, t – время.

Скорость – первая производная расстояния по времени:

_{при t0 = 2:}

Ускорение – вторая производная расстояния по времени:

_{при t0 = 2}

Задание 7. Найти пределы, используя элементарные способы раскрытия неопределенностей или правило Лопиталя:

а)

б)

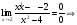
В соответствии с правилом Лопиталя:

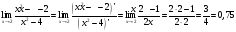
в)

Так как при х → 0 (первый замечательный предел), а также

первый замечательный предел, то

Задание 8. Построить график функции у =f(x), используя общую схему исследования функции. Определить абсолютный максимум и абсолютный минимум функции на отрезке [a,b]:

1) Область определения функции , точек разрыва нет;

Пересечение с осью х: у = 5.

Пересечение с осью у:

Тогда точки пересечения с осью у: х = 1, х = - 5.

Функция – кубическая парабола - является нечетной (график функции обладает симметрией относительно изменения знака аргумента), не периодична.

2) Проведем исследование функции с помощью первой производной:

Определим критические точки:

,

,

Исследуемая функция монотонно возрастает на интервале 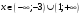и убывает на интервале .

3) Исследуeм функцию с помощью производной второго порядка, найдем точки перегиба графика функции и интервалы его выпуклости и вогнутости.

Следовательно, точка перегиба: (-1;0)

На интервале - функция выпуклая.

На интервале - функция вогнутая.

1

4) Определим асимптоты:

А) Вертикальные асимптоты:

Вертикальных асимптот нет (т.к. отсутствует такое значение х, при котором функция обращается в бесконечность).

Б) Наклонные асимптоты:

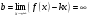
_{Построим график функции}

Функция непрерывна на отрезке [-2;2], поэтому имеет абмолютный минимум и абсолютный максимум. Данные для построения графика функции:

х	у
-2	27
-1,5	21,875
-1	16
-0,5	10,125
0	5
0,5	1,375
1	0
1,5	1,625
2	7

Из графика видно, что абсолютный максимум функция достигает в т. [-2; 27], а абсолютный минимум – в точке [1; 0].