Методические указания по выполнению контрольной работы №7

1. Понятие числового ряда. Необходимый признак сходимости.

Определение. Бесконечная сумма членов числовой последовательности {un} называется числовым рядом:

Здесьun ( n=1, 2, 3, … ) – n-ый член ряда.

Сумма конечного числа n первых членов ряда называется n-ой частичной суммой ряда:

Если существует конечный предел последовательности {Sn} частичных сумм S=lim Sn, то

n

этот предел называется суммой ряда, а сам ряд называется сходящимся. Если конечный предел частичных сумм не существует, то ряд называется расходящимся.

Необходимый признак сходимости ряда: ряд

может сходиться лишь в том случае, когда его общий член un при n является бесконечно малой величиной, т.е. un.

Если необходимое условие сходимости ряда не выполнено: lim un  0, либо предел не

n

существует, то ряд расходится (достаточный признак расходимости рядов).

Пример 1. Найти общий член ряда

Доказать ,что этот ряд расходится.

Решение. Последовательно рассмотрим члены ряда:

Подмечая закономерность, можно видеть, что общий член ряда выражается формулой

Представим общий член ряда в виде

Ясно, что при n un  , поскольку все сомножители-дроби , кроме первых трех, больше 1.

Отсюда следует, lim un  0: необходимое условие сходимости не выполнено, ряд расходится .

n

2. Положительные ряды.

Для исследования сходимости положительных рядов (т.е. рядов с неотрицательными членами: un) применяют достаточные признаки сходимости рядов. Среди них наиболее часто используют признаки сравнения, Даламбера, радикальный и интегральный признаки Коши

(Табл. 1).

Пример 2. Исследовать сходимость ряда

Решение. Применим первый признак сравнения. В качестве «эталонного» ряда возьмем обобщенный гармонический ряд

Показатель степени гармонического рядаp=4/5, поэтому «эталонный» ряд расходящийся. Члены исходного ряда для всех n превосходят соответствующие члены «эталонного» ряда:

Применяя 1 признак сравнения, заключаем, т.к. расходится «меньший» эталонный ряд, то расходится «больший» исходный ряд.

Пример 3. Исследовать сходимость ряда

Решение. Преобразуем общий член исходного ряда

Исходный ряд сравним с “эталонным” рядом

Это “геометрический ряд, он сходится, т.к. знаменатель прогрессииq=2/3<1. Поскольку

конечное число, отличное от 0, то в силу второго признака сравнения заключаем, что исходный ряд сходится.

Пример 4. Исследовать сходимость ряда

Решение. Применим признак Даламбера. Записываем n-ый член ряда

(n+1)-ый член получим, если в выражении un везде n заменим на (n+1):

Найдем предел отношения:

Пример 5. Исследовать сходимость ряда

Р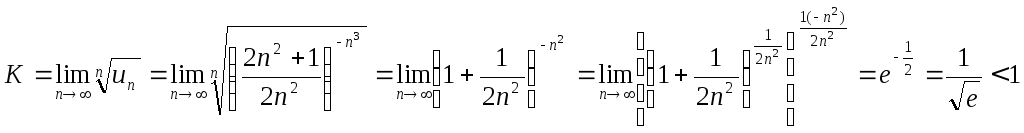ешение.Здесь удобно применить радикальный признак Коши:

Следовательно, ряд сходится. Подчеркнем, здесь использовали известный «замечательный» предел

Пример 6. Исследовать сходимость ряда

Решение.Рассмотрим функцию

Она при x2 положительная, непрерывная и монотонно убывает. (Заметим, что эта функция получается из выражения общего члена ряда при замене n на x). Можно применять интегральный признак. Исследуем сходимость несобственного интеграла:

Согласно интегрального признака, поскольку несобственный интеграл сходится , то сходится и исследуемый ряд.