
- •16 НеоИнт Неопределённый интеграл.
- •1. Понятие первообразной и неопределенного интеграла.
- •2. Свойства неопределённых интегралов.
- •3. Таблица основных неопределенных интегралов.
- •4. Метод интегрирования подстановкой
- •5. Интегралы группы четырёх.
- •6. Интегрирование по частям.
- •7. Интегрирование рациональных дробей.
- •8. Интегрирование тригонометрических выражений.
- •9. Интегрирование иррациональных выражений.
9. Интегрирование иррациональных выражений.
1. Интегралы вида
![]()
Пусть
![]() – общий знаменатель
– общий знаменатель
![]() .
.
Тогда
эффективна замена переменных:
![]()
2. Интегралы вида
![]()
Пусть
![]() – общий знаменатель
– общий знаменатель
![]() .
.
Тогда
эффективна замена
![]() .
.
Пример 11.
Взять интеграл

Сделаем замены:

В результате чего интеграл преобразуется к виду
![]()
Подынтегральное выражение разложим на простейшие дроби
![]()
Найдем выражение для
коэффициентов
![]() ,
для чего правую часть полученного
выражения приведем к общему знаменателю:
,
для чего правую часть полученного
выражения приведем к общему знаменателю:
![]()
Дроби равны, знаменатели равны, значит должны быть равны и числители
![]()
Сгруппируем правую часть
по степеням
![]() :
:
![]()
Полученное уравнение эквивалентно системе уравнений

Решая эту систему, получим:
![]()
Следовательно:
![]()
Интегрируя, получим:
![]()
Возвращаясь к старым переменным, получим:
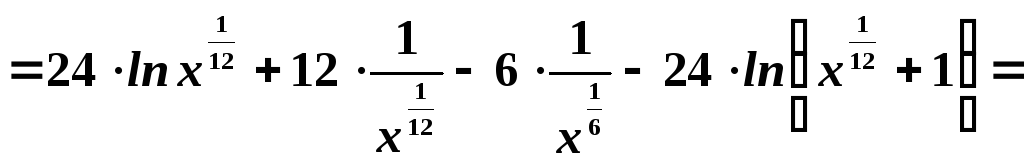
Преобразовывая, получим окончательно:

Пример 12.
Взять интеграл
![]() .
.
Сделаем замену:
![]() .
.
Выразим
![]() через
через
![]() :
:
![]()
Найдем дифференциал
![]() :
:
![]()
В результате чего наш интеграл примет вид:
![]()
Выполним преобразования:
![]()
Подынтегральное выражение представим в виде суммы элементарных дробей:
![]()
Аналогично предыдущему
примеру, запишем выражение для определения
коэффициентов
![]()
![]()
Возведем в квадрат скобки:
![]()
Перемножим скобки
![]()
Приведем подобные члены
![]()
Перегруппируем по степеням
![]()
![]()
Для определения коэффициентов
![]() получили систему
получили систему

Упростим третье уравнение

Преобразуем полученную систему

Решая ее, получим выражения
для коэффициентов
![]()
![]()
Подставим найденные значения
коэффициентов
![]() в наше уравнение
в наше уравнение
![]()
Проинтегрировав, получим:
![]()
Возвращаемся к "старой"
переменной
![]()

Упростим получившееся выражение
 .
.
Интегрирование рациональных функций, т.е интегрирование выражений вида:
![]()
В зависимости от конкретного вида выражения, существуют разные способы интегрирования.
1.
Выделение полного квадрата
![]()
2. Тригонометрические замены.

FVB
