физика / лекции / Лекция 13

8

Лекция 13. Электромагнитные колебания и волны.

[1] гл. 18, 20

План лекции

1. Свободные незатухающие колебания в колебательном контуре.

2. Свободные затухающие электромагнитные колебания.

3. Вынужденные электромагнитные колебания. Электрический резонанс.

4. Электромагнитные волны.

1.Свободные незатухающие колебания в колебательном контуре.

Среди электрических явлений особое место занимают электромагнитные колебания, при которых электрические величины (заряды, токи, электрические и магнитные поля) изменяются периодически. Для возбуждения и поддерживания электромагнитных колебаний требуются определенные системы, простейшей из которых является колебательный контур.

Колебательный контур - это цепь, состоящая из последовательно соединенных катушки индуктивностью L и конденсатора емкостью С.

Рассмотрим процесс возникновения электромагнитных колебаний в идеализированном колебательном контуре, в котором можно пренебречь сопротивлением соединительных проводов. Для возбуждения в контуре колебаний конденсатор предварительно заряжают, сообщая его обкладкам заряд q₀ от внешнего источника (рис.1).

В заряженном колебательном контуре устанавливаются свободные колебания, называемые электромагнитными. При этом колеблются значения всех электрических и магнитных величин.

В контуре возникают электромагнитные колебания, при которых происходит превращение энергии электрического поля в энергию магнитного поля и наоборот. Рисунок 2 представляет собой график зависимости заряда конденсатора от времени , , на котором значениям заряда в моменты времени сопоставлены соответствующие состояния колебательного контура (а; б; в; г; д).

Электромагнитные колебания во многом подобны механическим колебаниям, т.е. подобны описывающие их уравнения и их решения.

Запишем для контура 2-е правило Кирхгофа для произвольного момента времени: сумма падений напряжений равна сумме действующих в контуре эдс. В контуре действует только одна эдс - эдс самоиндукции , а падение напряжения происходит на конденсаторе, поэтому

где - мгновенное значение заряда на обкладках конденсатора.

Обозначим ;

- дифференциальное уравнение свободных электромагнитных колебаний.

Решением этого уравнения является выражение .

Таким образом, в идеальном колебательном контуре (рис.3) колебания заряда происходит по гармоническому закону (рис.4).

,

т.е. колебания тока опережают колебания заряда по фазе на когда ток достигает максимального значения, заряд и напряжение обращаются в нуль (и наоборот).

Т.к. собственная циклическая частота контура,

формула Томсона.

2. Свободные затухающие электромагнитные колебания.

Т.к. всякий проводник обладает сопротивлением, в процессе прохождения тока в колебательном контуре выделяется джоулево тепло, т.е. теряется энергия, поэтому свободные электромагнитные колебания в реальном контуре (рис. 5) всегда затухающие. Для такого контура

, где - падение напряжения на активном сопротивлении контура.

,

или .

Обозначим .

- дифференциальное уравнение свободных затухающих электромагнитных колебаний.

Решением этого уравнения является выражение .

циклическая частота собственных незатухающих колебаний;

циклическая частота собственных затухающих колебаний;

закон убывания амплитуды (рис.6), где - амплитуда при t=0.

Выясним физический смысл . Введем понятие времени реакции  - времени, за которое амплитуда уменьшается в е раз.

Таким образом,  есть величина, обратная .

Логарифмический декремент затухания - натуральный логарифм отношения 2-х амплитуд, отличающихся по времени на период.

За время  система совершит колебаний.

,

- число колебаний, за которые амплитуда уменьшается в е раз.

Добротность характеризует способность колебательного контура к затуханию колебаний:

Q.

Добротность пропорциональна числу колебаний, за которые амплитуда уменьшается в е раз.

Если Q велико, колебания затухают медленно (рис.7, ).

2. Вынужденные электромагнитные колебания. Электрический резонанс.

Свободные электромагнитные колебания происходят с частотой, определяемой параметрами контура , и , и в реальном колебательном контуре со временем затухают из-за потерь энергии. Чтобы получить незатухающие колебания, потери энергии необходимо компенсировать. Таким образом, для получения незатухающих электромагнитных колебаний необходимо ввести в контур э.д.с., периодически меняющуюся с течением времени по гармоническому закону:

,

где ₀ – амплитуда э.д.с.;  – циклическая частота вынуждающей э.д.с.

Вынужденными называются электромагнитные колебания, которые происходят под действием периодически изменяющейся эдс (рис.8).

т.к.,

- дифференциальное уравнение вынужденных электромагнитных колебаний.

Можно доказать, что решением этого уравнения является выражение:

.

Н а рис. 9 приведен график зависимости заряда конденсатора от времени в случае установившихся вынужденных электромагнитных колебаний.

Вынужденные колебания совершаются с такой же частотой , что и вынуждающая э.д.с. Экспериментально установлено, что изменение отстает в своем изменении от изменений э.д.с ; y - разность фаз колебаний и , сдвиг по фазе между изменением и .

Амплитудное значение заряда и определяются формулами:

.

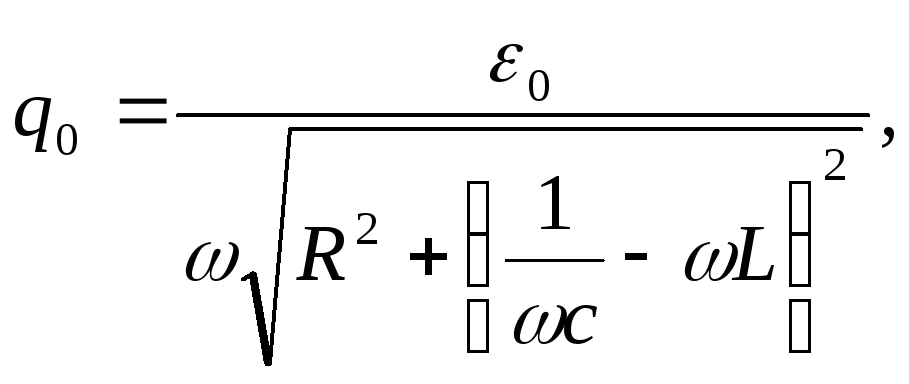
Т.к. можно найти w, при которой .

Расчеты показывают, что .

Электрический резонанс - явление резкого возрастания амплитуды вынужденных колебаний, когда частота вынуждающей эдс приближается к собственной частоте колебательного контура .

Чем больше сопротивление контура R, тем более полого располагается резонансная кривая (рис. 10).

2. Электромагнитные волны.

Электрический заряд, движущийся в пустоте равномерно (относительно ИСО), не излучает. Это очевидно из принципа относительности, согласно которому все ИСО равноправны. В системе, движущейся вместе с зарядом, он неподвижен, а неподвижные заряды не излучают. Поле заряда (электростатическое в его собственной системе и электромагнитное во всех других) движется вместе с ним. Если заряд под действием внешних сил движется с ускорением, поле, обладающее энергией, а значит массой и инертностью, как бы отрывается от заряда и излучается в пространство со скоростью света. Излучение происходит до тех пор, пока на заряд действует внешняя сила, сообщающая ему ускорение. Пример: синхротронное излучение, при энергиях  10⁷ эВ электроны излучают видимый свет, при 10⁹ эВ - рентгеновские лучи.

Движение заряда с ускорением меняет электрическое поле вблизи него. Это переменное электрическое поле, согласно теории Максвелла, порождает в окружающем пространстве взаимосвязанное с ним магнитное поле, которое, в свою очередь, являясь переменным, порождает в соседних областях пространства вихревое электрическое поле, в результате чего процесс с огромной скоростью распространяется в пространстве по всем направлениям (рис. 11).

Таким образом, если электрический заряд движется с ускорением (или колеблется), в окружающем пространстве, захватывая все большие области, возникает система взаимно перпендикулярных, периодически изменяющихся электрических и магнитных полей. Образуется электромагнитная волна, бегущая по всем направлениям от колеблющегося заряда.

Процесс распространения электромагнитных колебаний в пространстве называется электромагнитной волной. Главное условие излучения ЭМВ - наличие ускорения.

Векторы перпендикулярны друг другу и к направлению распространения и образуют с ним правовинтовую систему. Поскольку ЭМВ является поперечной (рис. 12). На расстояниях от источника, значительно превышающих длину волны, ЭМВ является плоской.

где скорость ЭМВ в вакууме,

.

Получим уравнение плоской ЭМВ (рис. 13).

Если в точке О , в точке М ;

- время, за которое волна пройдет расстояние от точки до точки .

Т.к. ,

,

где - волновой вектор.

В общем случае , .

Электромагнитное поле излучения было открыто сравнительно недавно, около 100 лет назад. За истекшее столетие это открытие привело к существенным изменениям в жизни общества. Большинство радиотехнических систем основано на непосредственном использовании электромагнитного поля, т.е. радиоволн для передачи информации (связь, вещание, телевидение) или извлечения ее (радиолокация, радиотелеизмерения и т.д.); собственно слово «радио» означает излучение.

Нет такой области человеческой деятельности, где радиотехника не применялась бы или не могла бы быть применена. Прогресс общества без радиотехники, радиоэлектроники просто невозможен. Радиоэлектронику используют в различных научных исследованиях, космических исследованиях, в авиации, на флоте, в медицине, метрологии, геологии, промышленности, сельском хозяйстве. В последнее время проводятся исследования возможности передачи солнечной энергии от космических фотоэлементов на Землю с помощью радиоволн, сконцентрированных в узкие пучки. Широко используются радиоволны в военном деле: радиолокация - для борьбы с самонаводящимися ракетами; для радиолокационной воздушной разведки и т.д.

В последнее время стало возможным получать высококачественные радиолокационные изображения земной поверхности и объектов, сравнимые по детальности с аэрофотоснимками.

Возможность использования радиосигналов для определения местоположения отражающих объектов (кораблей, самолетов, автомобилей) высказал еще А.С. Попов, которому мир обязан изобретением радиоприемника.

На основе систем радиопеленгации построены «автопилоты», системы «слепой» посадки самолетов в тумане и многие другие устройства.