
Лекция 12. Механические колебания и волны.
[1] гл. 18,19
План лекции
-
Гармонические колебания и их характеристики.
-
Свободные незатухающие механические колебания.
-
Свободные затухающие и вынужденные механические колебания.
-
Упругие волны.
-
Гармонические колебания и их характеристики.
Колебаниями называются процессы, которые характеризуются определенной повторяемостью во времени, т.е. колебания - периодические изменения какой-либо величины.
В зависимости от физической природы различают механические и электромагнитные колебания. В зависимости от характера воздействия на колеблющуюся систему различают свободные (или собственные) колебания, вынужденные колебания, автоколебания и параметрические колебания.
Колебания называются периодическими, если значения всех физических величин, изменяющихся при колебаниях системы, повторяются через равные промежутки времени.
Период - это время, за которое совершается одно полное колебание:
![]() ,
,
где
![]() - число колебаний за время
- число колебаний за время
![]() .
.
Частота колебаний - число полных колебаний, совершенных за единицу времени.
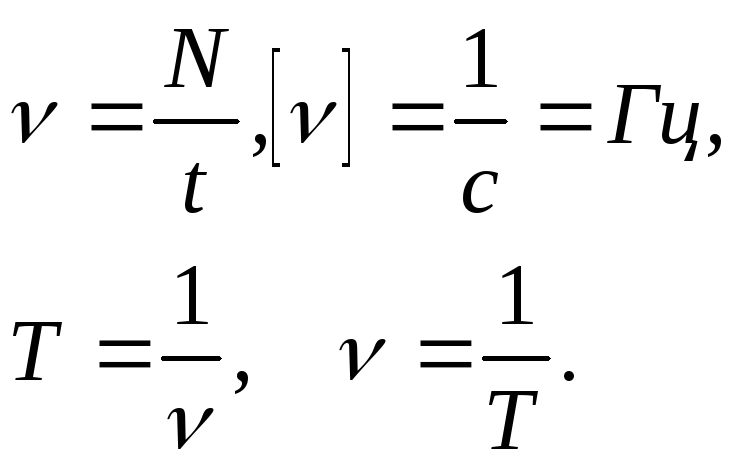
Циклическая или круговая частота - число полных колебаний, совершенных за время 2 (единиц времени):
![]() .
.
Простейшим типом колебаний являются гармонические колебания, при которых изменение величины происходит по закону синуса или косинуса (рис.1):
![]() ,
,
где
![]() - значение изменяющейся величины;
- значение изменяющейся величины;
![]() - амплитуда колебаний, максимальное
значение изменяющейся величины;
- амплитуда колебаний, максимальное
значение изменяющейся величины;
![]() - фаза колебаний в момент времени
- фаза колебаний в момент времени
![]() (угловая мера времени);
(угловая мера времени);
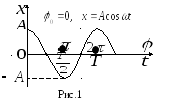 0
- начальная фаза, определяет значение
0
- начальная фаза, определяет значение
![]() в начальный момент времени при
в начальный момент времени при
![]() ,
, ![]() .
.
Колебательная система, совершающая гармонические колебания, называется гармоническим осциллятором.
Скорость и ускорение при гармонических колебаниях:

-
Свободные незатухающие механические колебания.
Свободными или собственными называются колебания, которые совершает система около положения равновесия после того, как она каким-либо образом была выведена из состояния устойчивого равновесия и представлена самой себе.
Как только тело (или система) выводится из положения равновесия, сразу же появляется сила, стремящаяся возвратить тело в положение равновесия. Эта сила называется возвращающей, она всегда направлена к положению равновесия, происхождение ее различно:
а) для пружинного маятника - сила упругости;
б) для математического маятника - составляющая сила тяжести.
Свободные или собственные колебания - это колебание, происходящие под действием возвращающей силы.
Если в системе отсутствуют силы трения, колебания продолжаются бесконечно долго с постоянной амплитудой и называются собственными незатухающими колебаниями.
Пружинный маятник - материальная точка массой m, подвешенная на абсолютно упругой невесомой пружине и совершающая колебания под действием упругой силы.
Рассмотрим динамику собственных незатухающих колебаний пружинного маятника.
![]() - по II закону Ньютона,
- по II закону Ньютона,
![]() по закону Гука,
по закону Гука,
где k – жесткость,
![]() ;
;
![]() или
или![]() .
.
Обозначим
![]() циклическая частота собственных
колебаний.
циклическая частота собственных
колебаний.
![]() - дифференциальное уравнение свободных
незатухающих колебаний.
- дифференциальное уравнение свободных
незатухающих колебаний.
Решением этого уравнения является
выражение:
![]() .
.
![]() период
колебаний пружинного маятника.
период
колебаний пружинного маятника.
При гармонических колебаниях полная
энергия системы остается постоянной,
происходит непрерывный переход
![]() в
в
![]() и наоборот.
и наоборот.
 Математический
маятник - материальная точка, подвешенная
на невесомой нерастяжимой нити (рис.2).
Математический
маятник - материальная точка, подвешенная
на невесомой нерастяжимой нити (рис.2).
Можно доказать, что в этом случае
![]()
Пружинный и математический маятники являются гармоническими осцилляторами (как и колебательный контур). Гармоническим осциллятором называется система, описываемая уравнением:
![]() .
.
Колебания гармонического осциллятора являются важным примером периодического движения и служат приближенной моделью во многих задачах классической и квантовой физики.
