ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ФИЗИКИ

Определение скорости снаряда методом крутильных колебаний

Методические указания к лабораторной работе № 9

Ростов-на-Дону 2008

Составители: С.М. Максимов, В.Л. Литвищенко, Н.В. Пруцакова

УДК 530.1

Определение скорости снаряда методом крутильных колебаний: Метод. указания. - Ростов н/Д: Издатель­ский центр ДГТУ, 2008. - 12 с.

Указания содержат краткое изложение устройства и принципа действия крутильного баллистического маятника.

Методические указания предназначены для выполнения лабораторной работы студентами всех форм обучения в лабораторном практикуме по физике (раздел механика).

Печатается по решению методической комиссии факультета «Автоматизация и информатика»

Научный редактор проф., д.т.н. В.С. Кунаков

Рецензент доц., к.ф.-м.н. Р.И. Смирнова

© С.М. Максимов, В.Л. Литвищенко, Н.В. Пруцакова, 2008

©

Издательский центр ДГТУ, 2008

Лабораторная работа № 6

Определение скорости снаряда методом крутильных колебаний

Цель работы: Определить скорость поступательного движения снаряда в момент попадания его в мишень крутильного баллистического маятника.

Краткая теория: основы кинематики и динамики вращательного движения твердого тела. Законы сохранения

При вращении твердого тела вокруг неподвижной оси отдельные точки тела описывают окружности, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиусаR и за бесконечно малый промежуток времени dt совершает поворот на угол (малый поворот рассматривается как вектор, модуль которого равен углу поворота dφ, а направление подчиняется правилу правого винта (рис. 1)).

Угловой скоростью называется векторная физическая величина, определяемая первой производной угла поворота по времени:

Рис. 1

.

Вектор , как и вектор , направлен вдоль оси вращения по правилу правого винта (рис. 1).

Угловым ускорением называется векторная физическая величина, определяемая первой производной угловой скорости по времени:

.

При ускоренном движении вектор по направлению совпадает с(рис.2, а), а при замедленном - инаправлены противоположно друг другу (рис. 2,б).

а

б

Рис. 2

М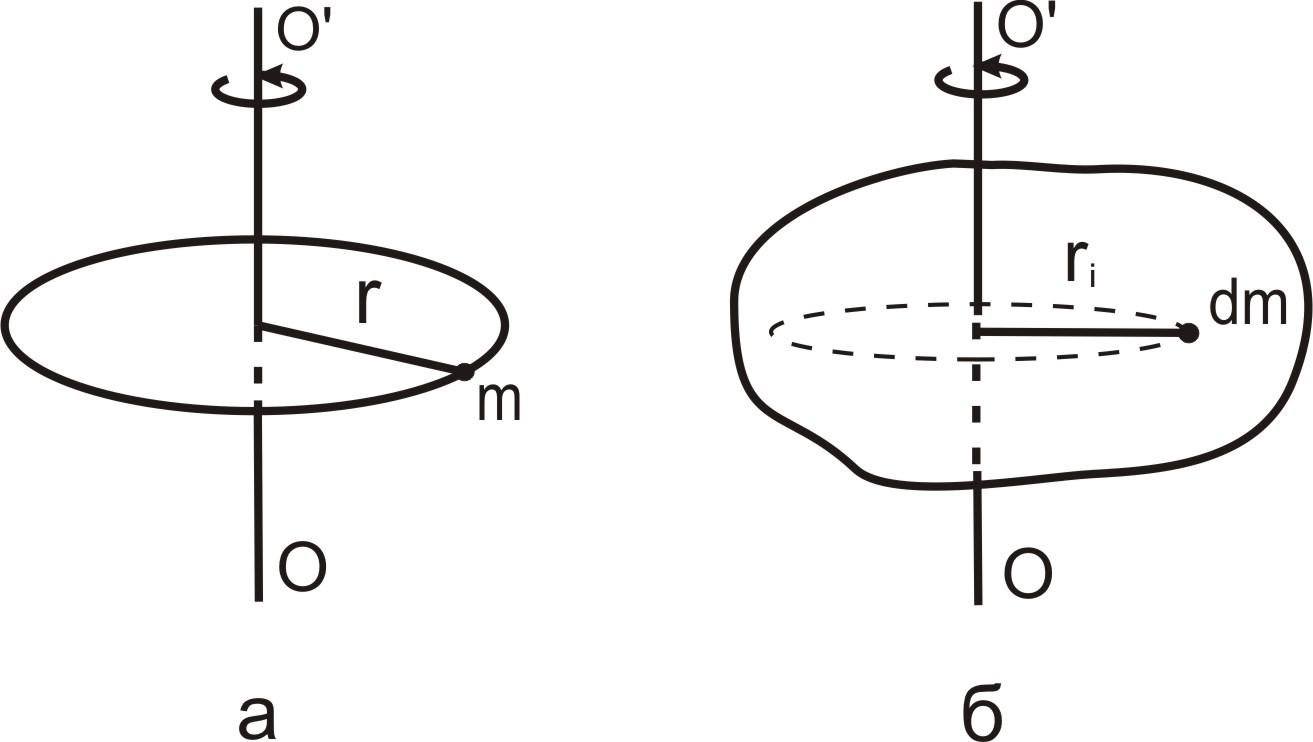оментом инерцииI материальной точки называется скалярная физическая величина, определяемая произведением ее массы m на квадрат радиуса окружности r, по которой она может двигаться относительно некоторой произвольно выбранной оси ОО^' (рис. 3,а).

Е

Рис. 3

сли твердое тело, вращающееся относительно некоторой произвольно выбранной оси ОО', представить в виде системы материальных точек массойdm, и просуммировать моменты инерции этих, так называемых, элементарных масс, то получим

момент инерции всего тела

,

где r_i – радиус вращения i – той элементарной массы, а интеграл берется по всему объему тела (рис. 3,б). Для однородных тел, для которых плотность (гдеm – масса тела, а V – его объем, т.е. плотность определяется массой, заключенной в единице объема), момент инерции будет вычисляться по формуле

.

Теорема Штейнера

Если известен момент инерции тела относительно оси ОО', проходящей через центр масс тела (обозначим его I_o), то момент инерции тела относительно любой параллельной ей оси ZZ'

(обозначим его I ) равен

,

где m – масса тела, d – расстояние между осями (рис. 4).

Рис. 4

М

Рис. 5

оментом силы относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиус-вектора, проведенного из точки О в точку А приложения силы, на силу(рис. 5):.

Модуль момента силы равен , гдеα – угол между и,- плечо силы(l - длина перпендикуляра, опущенного из точки О на направление действия силы (рис. 5)).

Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси: , то есть направлениесовпадает с направлением(рис. 4). Моментом силыM_z относительно неподвижной оси ZZ' называется проекция этого момента на данную ось.

М

Рис. 6

оментом импульса материальной точки относительно произвольной точки О называется физическая величина, определяемая векторным произведением радиус-вектора этой материальной точки, проведенного из точки О, на величину ее импульса(m - масса материальной точки, – ее скорость при поступательном движении или линейная скорость ее при вращательном движении), то есть . Векторнаправлен так же, как и вектор угловой скорости, т. е. вдоль оси вращения, согласно правилу правого винта (рис. 6).

Если твердое тело, вращающееся вокруг некоторой неподвижной оси ZZ', представить в виде совокупности элементарных масс, и спроектировать моменты импульсов всех этих элементарных масс на это направление, получим момент импульса тела L_z относительно этой оси. Суммирование производим по всем элементарным массам m_i, на которые разбивается тело.

,

так как , гдеω - угловая скорость вращения тела, I – момент инерции твердого тела. В общем случае .

Закон сохранения момента импульса: момент импульса замкнутой системы тел не меняется со временем, причем это утверждение справедливо для момента импульса, взятого относительно любой точки инерциальной системы отсчета. Этот закон выполняется только в инерциальных системах отсчета.

Кинетическая энергия измеряется работой, которую тело может произвести благодаря инерции при затормаживании тела до полной остановки. Кинетическая энергия материальной точки массы m при поступательном движении со скоростью V определяется фор-мулой Е_к = . При вращательном движении роль массы m выпол-няет момент инерции I, а вместо скорости V выступает угловая скорость ω, и формула кинетической энергии при вращательном движении материальной точки приобретает вид: E_{к вращ} .

Потенциальная энергия измеряется работой, которую тело может совершить при перемещении его из одного простран-ственного положения в другое. Так, потенциальная энергия тела массы m, поднятого на высоту h над поверхностью Земли E_пот = mgh. Потенциальная энергия упруго деформированной пружины Е_пот =, где k – коэффициент упругости, х – деформация пружины. Потенциаль-ная энергия при закручивании стержня Е_пот =, гдеD – константа, зависящая от упругих свойств стержня при его кручении (так называ-мый модуль кручения), α_о – угол деформации при закручивании.

Закон сохранения механической энергии гласит: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остается постоянной, возможны лишь превращения кинетической энергии в потенциальную и наоборот. Напомним, что консервативными называют силы, работа которых по замкнутой траектории равна нулю. Так, при закручивании упругого стержня (нити) закон сохранения энергии может быть записан как .

Описание экспериментальной установки

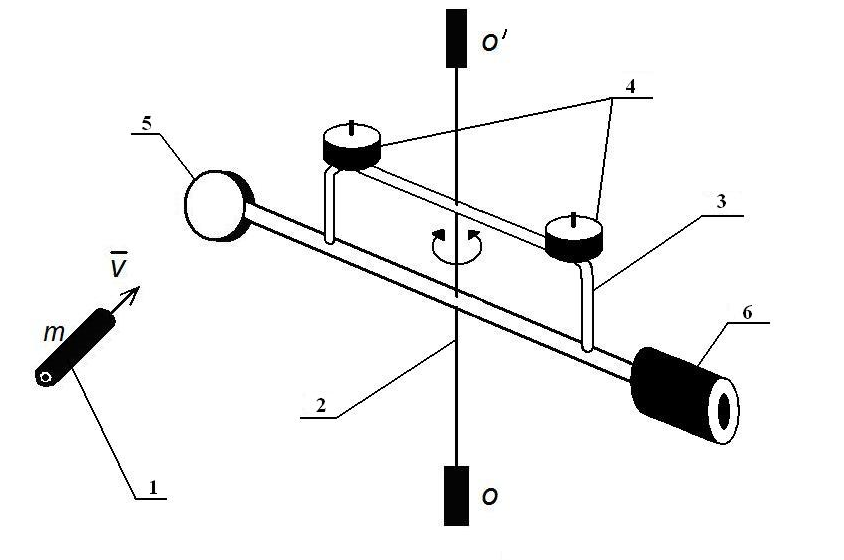
Используемый в данной работе крутильный баллистический маятник, внешний вид которого показан на рис. 7, представляет собой горизонтально расположенный стержень, подвешенный на упругой нити. С одной стороны стержня (см. рис. 8) находится мишень, а с другой стороны – ее противовес.

Рис. 7. Внешний вид установки для измерения скорости снаряда методом крутильных колебаний

1 – снаряд 2 – упругая нить 3 – рамка

4 – съемные грузы (m1) 5 5 – мишень 6 6 – противовес

Рис. 8. Схематическое устройство крутильного баллистического маятника

На стержне закреплена рамка с двумя съемными грузами m₁, что позволяет изменять момент инерции колебательной системы. После попадания снаряда в мишень, система начинает совершать колебательное движение вокруг вертикальной оси ОО^'.

Теория метода измерения

Запишем законы сохранения момента импульса и энергии, пренебрегая, ввиду малости его значения, моментом сил трения, в следующем виде:

mV= (I₁ + m²)  (1) , (2)

где m - масса снаряда,

V - скорость снаряда в момент попадания его в мишень,

- расстояние от оси вращения ОО^' до точки попадания снаряда в мишень,

I₁ - момент инерции маятника,

 - угловая скорость маятника в момент попадания снаряда в мишень,

₀ - наибольший угол отклонения стержня от положения равновесия,

D - модуль кручения.

Выразим ² из уравнений (1) и (2)

ω² = (3) ω² = . (4)

Приравняв правые части (3) и (4), получаем выражение для V² в виде

.

Для данной конкретной установки ml² « I₁, и формула для определения скорости снаряда принимает вид:

. (5)

Для исключения величины D воспользуемся основным уравнением динамики вращательного движения твердого тела

,

где М - момент сил упругости, ε – угловое ускорение мишени со снарядом.

В свою очередь, M = – Dα. Знак (-) указывает на то, что этот момент возвращает систему в состояние устойчивого положения равновесия. Тогда

I₁ε = –Dα . (6)

Здесь α – угол поворота стержня с закрепленной на нем мишенью. Учитывая, что угловое ускорение ε = , перепишем уравнение (6) в виде

.

Введя обозначение , приходим к уравнению

.

А это - дифференциальное уравнение гармонических колебаний и его решением является уравнение вида: α = α₀ sin ωt. Поскольку период колебаний: T = , то формула для определения периода колебаний крутильного баллистического маятника с грузамиm₁ запишется в виде:

T₁ =, (7) откуда. (7а)

Уменьшим момент инерции системы на величину ∆I, сняв оба груза m₁. Согласно теореме Штейнера, можно найти изменение момента инерции системы ∆I = 2(I₀ + m₁d²), где – момент инерции грузов - дисков (массойm₁ и радиусом r) относительно собственной оси симметрии, через d обозначено расстояние от оси ОО^' до оси грузов, получим значение нового периода колебаний системы Т₂ для системы со снятыми грузами m₁:

T₂ =, (8) откуд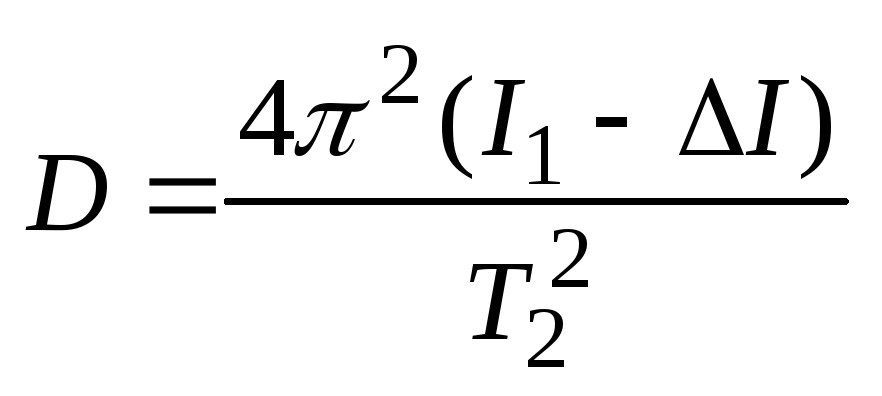а. (8а)

Совместное рассмотрение (7а) и (8а) позволяет получить значение I₁:

.

Для используемой нами установки m₁r ² « 2 m₁d ², поэтому

. (9)

Подставляя значения D и I₁ в формулу (5), получаем рабочую формулу для определения скорости снаряда:

. (10)

Здесь T₁ и T₂ – периоды колебаний нагруженного и ненагруженного баллистического крутильного маятника соответственно; m₁ - масса съемных грузиков, m – масса снаряда; l – расстояние от оси вращения системы до следа снаряда на мишени; d – расстояние от съемных грузов m₁ до оси вращения ОО', α₀ – максимальный угол поворота стержня.