Михалкович С.С. Основы программирования

В программировании рекурсия – это описание подпрограммы, содержащее прямой или косвенный вызов этой подпрограммой самой себя. Если подпрограмма р вызывает себя в своем теле, то такая рекурсия называется прямой, если же подпрограмма р вызывает подпрограмму q, которая прямо или косвенно вызывает р, то такая рекурсия называется косвенной. Рекурсией также называют процесс выполнения рекурсивной подпрограммы.

2.2 Простые примеры использования рекурсии

Рассмотрим несколько примеров рекурсивных подпрограмм.

Пример 1. procedure p; begin

write(1);

p; end;

При вызове процедуры p произойдёт рекурсивное зацикливание: будет выводиться 1, после чего процедура снова будет вызывать себя и т.д. до бесконечности. Поскольку при каждом вызове процедуры на программный стек помещается ее запись активации, то в конце концов программный стек переполнится, и программа завершится с ошибкой. Таким образом, чтобы рекурсия завершалась, необходимо, чтобы рекурсивный вызов происходил не всегда, а лишь при выполнении некоторого условия.

Пример 2.

procedure p(n: integer); begin

write(n,' ');

if n>0 then p(n-1); end;

При вызове p(5) вначале выведется 5, после чего вызовется p(4), выведется 4 и вызовется p(3) и т.д. до вызова p(0), который выведет 0 и, поскольку условие n>0 станет ложным, рекурсия завершится. Итак, в результате вызова p(5) на экран будет выведено

5 4 3 2 1 0

Таким образом, использование рекурсии позволяет заменить цикл. Отметим,

что в простых примерах такая замена неэффективна, так как накладные расходы на рекурсивный вызов процедур (копирование параметров на программный стек, запоминание адреса возврата и т.д.) намного превосходят затраты на организацию цикла.

23

Пример 3.

procedure p(n: integer); begin

if n>0 then p(n-1); write(n,' ');

end;

При вызове p(5) вначале проверится условие n>0 и, поскольку оно истинно, вызовется p(4), затем p(3) и т.д. до p(0). Так как при вызове p(0) условие n>0 уже не выполняется, то осуществится вывод 0 и произойдет выход из вызова p(0) в вызов p(1) сразу после условного оператора. Далее осуществится вывод 1 и выход из вызова p(1). Процесс возврата из уже сделанных рекурсивных вызовов продолжится, пока не будет осуществлен выход из вызова p(5). В результате на экран будет выведено

0 1 2 3 4 5

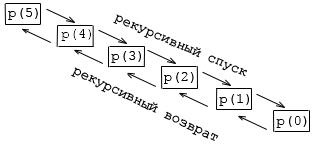
Схема рекурсивных вызовов в примерах 2 и 3 изображена на рисунке:

Процесс рекурсивных вызовов называется рекурсивным спуском, а процесс возврата из них – рекурсивным возвратом. Глубиной рекурсии называется мак-

симальное число вложенных рекурсивных вызовов (в примерах 2 и 3 глубина рекурсии равна 5). Число вложенных рекурсивных вызовов в данный момент выполнения программы называется текущим уровнем рекурсии.

Отметим, что в примере 2 действия осуществляются на рекурсивном спуске, поэтому порядок действий – прямой (в порядке вызова рекурсивных процедур). В примере 3, напротив, действия осуществляются на рекурсивном возврате, т.е. откладываются до достижения наивысшей глубины рекурсии, после чего начинают выполняться в порядке, обратном порядку вызова.

Реализуем рекурсивные функции из примеров в начале пункта. Пример 4. Вычисление n!

Реализация повторяет рекурсивное определение n!, данное в начале главы: function Nfact(n: integer): integer;

begin

if n=0 then

Result:=1

else Result:=n*Nfact(n-1); end;

24

Пример 5. Вычисление an .

Рассмотрим рекурсивное определение an , которое является более эффективным, чем приведенное в начале главы, и, кроме того, учитывает случай n < 0 :

1, если n = 0,

(an / 2 )2 , если n > 0, n −четное, an =

a an−1, если n > 0, n −нечетное,

1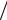an , если n < 0.

Реализация также не вызывает затруднений:

function Power(a: real; n: integer): real; begin

if n=0 then

Result:=1

else if n<0 then

Result:=Power(a,-n) else if Odd(n) then

Result:=a*Power(a,n-1)

else Result:=Sqr(Power(a,n div 2)); end;

При программировании рекурсивных подпрограмм следует следить за глубиной рекурсии: она не должна быть очень большой, чтобы программный стек не переполнился.

Нетрудно видеть, что при вычислении a16 глубина рекурсии равна 5:

При вычислении же a15 функция Power последовательно вызывается для аргументов 15, 14, 7, 6, 3, 2, 1, 0, и глубина рекурсии составляет 7.

Недостаток данного алгоритма состоит в том, что переменная a не меняется, но передается в каждый рекурсивный вызов. Сделаем переменную a глобальной по отношению к рекурсивной функции, для чего окаймим ее нерекурсивной функцией с параметрами a и n, осуществляющей в своем теле стартовый вызов рекурсивной функции:

function Power(a: real; n: integer): real;

function Power0(n: integer): real; begin

if n=0 then

Result:=1

25

else if Odd(n) then

Result:=a*Power0(n-1);

else Result:=Sqr(Power0(n div 2)); end;

begin

Result:=Power0(n); end;

Пример 6. Минимум в массиве.

Чтобы найти минимум в массиве из n элементов, достаточно найти минимум в массиве из первых n – 1 элементов, после чего выбрать минимальный из этого минимума и последнего элемента массива. Если в массиве всего один элемент, то он – минимальный.

Запишем данный алгоритм в виде рекурсивной функции MinA:

A[n], n =1,

MinA( A, n) = MinA( A[n], MinA( A, n −1)), n >1.

Реализация повторяет рекурсивное определение:

function MinA(const A: RArr; n: integer): real; begin

if n=1 then Result:=A[n] else

begin

Result:=MinA(A,n-1); if A[n]<Result then

Result:=A[n];

end; end;

Здесь RArr – тип вещественного массива, индексируемого от единицы. Отметим, что массив A не меняется при передаче в каждый рекурсивный вызов, поэтому следует воспользоваться приемом из предыдущего примера: окаймить функцию MinA нерекурсивной функцией и сделать параметр A глобальным по отношению к MinA.

Сделаем несколько замечаний, касающихся рекурсивных подпрограмм.

Замечание 1. При каждом рекурсивном вызове на программный стек помещается запись активации подпрограммы. Поэтому если количество рекурсивных вызовов большое или локальные переменные рекурсивной процедуры имеют большой размер, то программный стек может переполниться и возникнет ошибка времени выполнения программы.

Замечание 2. Накладные расходы на рекурсивные вызовы достаточно велики, поэтому если есть явное нерекурсивное решение, то следует предпочесть его.

26

Замечание 3. Можно доказать, что любая прямая рекурсия может быть заменена итерацией.

2.3 Доказательство завершимости рекурсии

Как показать, что при вызове пряморекурсивной подпрограммы не происходит рекурсивного зацикливания, то есть рекурсивный вызов завершим? В самом простом случае с каждым рекурсивным вызовом связывается целое число n. Предположим, что рекурсия завершается, когда n ≤ 0 . Если нам удастся показать, что при каждом рекурсивном вызове n уменьшается, то рекурсивный вызов завершим. Именно поэтому в большинстве рекурсивных подпрограмм удобно использовать целый параметр n, который при каждом рекурсивном вызове уменьшается на 1, и завершать рекурсию, когда данный параметр становится равным 0.

2.4 Формы рекурсивных подпрограмм

Выделим следующие виды пряморекурсивных подпрограмм. 1) Действия осуществляется на рекурсивном спуске.

procedure p(n); begin

S(n);

if B(n) then p(n-1) end;

2) Действия осуществляются на рекурсивном возврате. procedure p(n);

begin

if B(n) then p(n-1)

S(n); // отложенные действия end;

3) Действия осуществляются и на рекурсивном спуске, и на рекурсивном возврате.

procedure p(n); begin

S1(n);

if B(n) then p(n-1) S2(n);

end;

Данный вид рекурсии удобно представлять себе следующим образом. Мы спускаемся по лестнице с пронумерованными ступеньками (n – номер ступеньки), делая шаг на каждую ступеньку, пока выполняется условие B(n), после чего возвращаемся в начальную точку. Перед тем, как совершить следующий шаг, мы выполняем действие S1(n) и обязуемся выполнить действие S2(n) когда будем воз-

27

вращаться. Таким образом, действия на рекурсивном спуске совершаются в прямом порядке, а обещанные действия осуществляются на рекурсивном подъеме в порядке, обратном порядку обещаний.

4) Каскадная рекурсия. procedure p(n); begin

S(n)

if B1(n) then p(n-1); if B2(n) then p(n-1);

end;

5) Удаленная рекурсия.

function f(i: integer): integer; begin

if B1(n) then Result:=...

else Result:=f(f(i-1)); end;

В этом виде рекурсии результат рекурсивного вызова является параметром другого рекурсивного вызова. Наиболее известным примером удаленной рекур-

сии является функция Аккермана:

m +1, если n = 0,

A(n, m) = A(n −1,1), если n > 0, m = 0,

A(n −1,A(n, m −1)), если n > 0, m > 0.

В последних двух видах рекурсии рекурсивные вызовы образуют древовидную структуру.

2.5 Пример плохого использования рекурсии

Пример 7. Пример плохого использования рекурсии. Числа Фибоначчи. Как известно, определение чисел Фибоначчи рекурсивно:

1, n =1,2,

fn = fn−1 + fn−2 , n > 2.

Данное определение легко переводится в рекурсивную функцию: function Fib(n: integer): integer;

begin

if (n=1) or (n=2) then Result:=1

else Result:=Fib(n-1)+Fib(n-2); end;

28

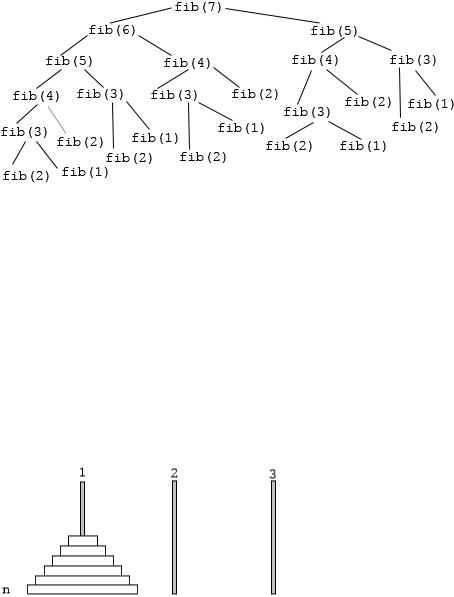
Однако, такое «лобовое» решение крайне неэффективно, поскольку содержит большое количество повторяющихся вычислений. Изобразим дерево рекурсивных вызовов для вызова Fib(7):

Из рисунка видно, что, например, Fib(5) вычисляется дважды, Fib(4) – трижды, Fib(3) – 5 раз и т.д., то есть количество повторных вызовов представляет собой, по иронии судьбы, последовательность чисел Фибоначчи!

2.6 Более сложные примеры использования рекурсии

Пример 8. Ханойские башни.

Это – классический пример задачи, у которой имеется простое рекурсивное решение, а нерекурсивное решение является существенно более громоздким и дает лишь незначительный выигрыш в эффективности.

Задача состоит в следующем. Имеется три штыря, на одном из которых лежит пирамида из n дисков, причем, меньшие диски лежат на больших (см. рисунок).

Требуется, перекладывая по одному диску на соседние штыри, переложить всю пирамиду с одного штыря на другой за наименьшее количество ходов. При этом запрещается класть больший диск на меньший.

Сведем задачу с n дисками к задаче с n – 1 дисками (фактически, применим метод математической индукции по числу дисков). Пусть нам требуется переложить пирамиду из дисков со штыря с номером f (from) на штырь с номером t (to), используя штырь w (work) в качестве вспомогательного. Для этого необходимо вначале переложить пирамиду из n – 1 диска со штыря f на штырь w, используя штырь t в качестве вспомогательного, затем переместить оставшийся диск со штыря f на штырь t и, наконец, переложить пирамиду из n – 1 диска со штыря w на штырь t, используя штырь f в качестве вспомогательного.

29

procedure MoveTown(n,f,t,w: integer); begin

if n=0 then exit; MoveTown(n-1,f,w,t); MoveDisk(f,t); MoveTown(n-1,w,t,f);

end;

Процедура MoveDisk, обеспечивающая перемещение одного диска, либо выдает текстовую информацию о том, с какого на какой диск было осуществлено перемещение, либо перемещает диск графически, меняя рисунок с изображениями штырей и дисков, подобный приведенному в начале данного примера.

Нетрудно показать, что глубина рекурсии равна n, а количество перемещений дисков составляет 2n −1.

Пример 2. Сгенерировать все перестановки длины n.

Заполним массив тождественной перестановкой. Будем менять первый элемент с каждым последующим, включая себя, после этого совершать те же действия с оставшейся частью массива и менять элементы обратно:

for i:=1 to n do begin

Swap(A[i],A[1]);

...

Swap(A[i],A[1]); end;

В итоге каждый элемент побывает на первом месте. Вместо многоточия вызовем аналогичную процедуру для элементов со второго по последний. Таким образом, мы реализовали следующую идею: получить все перестановки n элементов можно, поставив на первое место каждый элемент и дописав к нему все перестановки из оставшихся элементов. Очень важным шагом здесь является последний оператор цикла, возвращающий обратно элемент, переставленный на первом шаге цикла. Это гарантирует, что в начале каждой итерации цикла мы имеем дело с одной и той же перестановкой.

Поскольку рекурсивные вызовы необходимо совершать для элементов с индексами от 2 по n, затем от 3 по n и т.д., в качестве параметра рекурсивной процедуры будем передавать k – начальный индекс переставляемого элемента (таким образом, перестановка будет совершаться для элементов с номерами от k до n). В результате наша рекурсивная процедура примет вид:

procedure Permutation0(k: integer); var i: integer;

begin

for i:=k to n do begin

30

Swap(A[i],A[k]);

...

Permutation0(k+1);

Swap(A[i],A[k]); end;

end;

Очевидно, при k=n рекурсию надо завершать и выдавать полученную перестановку. Приведем итоговую процедуру, считая, что для вывода массива A длины n составлена процедура Print(A,n).

procedure Permutation(n: integer); var A: IArr;

procedure Permutation0(k: integer); var i: integer;

begin

for i:=k to n do begin

Swap(A[i],A[k]); if k=n then

Print(A,n)

else Permutation0(k+1); Swap(A[i],A[k]);

end; end;

var i: integer; begin

for i:=1 to n do

A[i]:=i;

Permutation0(1); end;

2.7 Быстрая сортировка

Алгоритм быстрой сортировки – один из самых производительных и часто используемых алгоритмов сортировки. Основная идея алгоритма быстрой сортировки состоит в следующем. На первом шаге выбирается некоторый опорный элемент x, относительно которого переупорядочиваются остальные элементы массива. Переупорядочение осуществляется следующим образом: все элементы, меньшие x, переставляются перед x, а больше или равные x – после x. В итоге массив оказывается разбит на две части: элементы, меньшие x, и элементы, большие или равные x. Затем к первой и второй частям рекурсивно применяется алгоритм быстрой сортировки до тех пор, пока в каждой части не останется по одному элементу. Желательно выбрать элемент x таким, чтобы количество элементов в

31

первой и второй части было примерно одинаковым (в идеале отличалось бы на 1 – в этом случае элемент x называется медианой массива). Однако, поиск медианы массива – достаточно долгий алгоритм, поэтому обычно в качестве элемента x выбирают любой элемент массива, например, средний.

Рассмотрим алгоритм подробнее. После выбора опорного элемента x введем два индекса i и j, указывающие соответственно на первый и последний элементы массива A. Увеличивая i, найдем элемент A[i], не меньший x. Затем, уменьшая j, найдем элемент A[j], не больший x. Такие элементы всегда найдутся: в крайнем случае, таким элементом будет сам элемент х. Поменяем элементы A[i] и A[j] местами, после чего увеличим i на 1 и уменьшим j на 1. Продолжим эти действия до тех пор, пока i не окажется больше j. В этот момент все элементы A[1]..A[j] меньше или равны x, а все элементы A[i]..A[n] - больше или равны x. Теперь применим наш алгоритм рекурсивно к подмассивам A[1]..A[j] и A[i]..A[n]. Процесс рекурсивных вызовов прекращается, если подмассив состоит из одного элемента.

Рассмотрим конкретный пример. Пусть массив A размера n=9 имеет вид:

Выберем в качестве x средний элемент A[5]=4 и положим i=1, j=n. Увеличивая i, найдем элемент A[i]>=x (это элемент A[2]=7) и уменьшая j найдем

Поменяем их местами и передвинем индексы i и j соответственно вперед и назад:

Аналогично поменяем местами элементы 6 и 3, затем 9 и 4. В результате индекс i станет больше индекса j:

Следует обратить внимание на то, что i может быть больше j на 1 или на 2, а также на то, что опорный элемент в преобразованном массиве может поменять свое место.

Итак, мы разделили массив на две части. Часть элементов с номерами от 1 до j меньше или равна x, а часть элементов с номерами от j до n – больше или равна x. Осталось рекурсивно применить алгоритм быстрой сортировки к обеим частям.

Ниже приводится код алгоритма:

32