11

Лекция 7. Волновая оптика.

[1] гл.22-25

План лекции

1. Интерференция света от двух когерентных источников. Кольца Ньютона.

2. Дифракция света. Дифракция Фраунгофера на дифракционной решетке.

3. Дисперсия света. Опыт Ньютона.

4. Поляризация света при отражении и преломлении. Законы Брюстера и Малюса.

1. Интерференция света от двух когерентных источников. Кольца Ньютона.

Раздел физики, в котором рассматриваются вопросы, связанные с изучением природы света, закономерностями его испускания, распространения и взаимодействия с веществом, называется оптикой.

В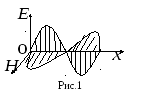волновой оптике рассматриваются оптические явления, в которых проявляется волновая природа света (явления интерференции, дифракции, поляризации и дисперсии). Так как свет представляет собой электромагнитные волны, то в основе волновой оптики лежат уравнения Максвелла и вытекающие из них соотношения для электромагнитных волн.

Свет представляет собой бегущую волну, в которой напряженность электрического и магнитного полей изменяются по гармоничному закону (рис.1). Видимый диапазон световых волн заключен в интервале .

иизменяются по гармоническому закону:

где – волновое число;– длина волны.

На основании опытных данных установлено, что физическое, фотохимическое и другие действия света вызываются колебаниями вектора напряженности электрического поля, поэтому вектор получил название светового вектора;–амплитуда светового вектора.

Интерференция света – это явление наложения когерентных волн, в результате которого происходит перераспределение энергии волн в пространстве и образование чередующихся максимумов и минимумов интенсивности.

Необходимое условие интерференции волн – их когерентность.

Когерентность – это согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов.

Когерентные волны – это волны одинаковой частоты, колебания в которых происходят с постоянной разностью фаз.

Трудность наблюдение интерференции обусловлена тем, что световые волны, излучаемые различными независимыми друг от друга источниками света всегда некогерентны, поскольку атомы этих источников испускают свет в разных непрерывно меняющихся фазах. Отдельные атомы излучают цуги волн длительностью порядка 10^-8с и протяженностью около 3 м.

Фаза нового цуга никак не связана с фазой предыдущего.

Когерентные световые волны можно получать, разделив (с помощью отражений или преломлений) волну, излучаемую одним источником, на две части. Если заставить эти две волны пройти разные оптические пути, а потом наложить их друг на друга, наблюдается интерференция. Область, в которой перекрываются когерентные волны, называется полем интерференции.

Один из первых способов получения когерентных световых волн предложил французский физик Огюст Френкель.

Б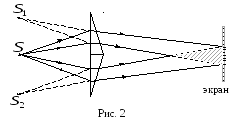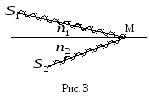ипризма Френеляпредставляет собой изготовленные из одного куска стекла две призмы с малым преломляющим углами и имеющие общее основание (рис.2). Волновой фронт света, исходящего от источникаS, с помощью призм разделяется на 2 части, представляющие собой когерентные световые волны, исходящие из мнимых источникови, лежащих в одной плоскости сS.

Представим себе, что две когерентные волны, испущенные точечными когерентными источниками и, накладываются друг на друга в точке(рис.3). Первая волна в среде с показателем преломленияпрошла путь, а вторая – путьв среде с показателем преломления. Выясним условия, определяющие интерференционный максимум или минимум в данной точке.

–оптическая длина пути, где– геометрическая длина пути;

–оптическая разность хода.

Если оптическая разность хода содержит целое число (m) длин волн, то в данную точку волны приходят в одинаковой фазе, и при их наложении происходит усиление света (рис. 4 а).

Максимум интерференциинаблюдается в точках, для которых

, ().

Если в оптической разности хода световых лучей до данной точки укладывается целое число длин волн в вакууме , то в этой точке пространства наблюдается интерференционный максимум.

Если в оптической разности хода содержится нечетное число длин полуволн, то в данную точку волны приходят в противофазе и гасят друг друга, происходит ослабление света (рис. 4 б).

Минимум интерференциисоответствует условию:

, ().

Если в оптической разности хода световых лучей до данной точки укладывается нечетное число длин полуволн в вакууме , то в этой точке пространства наблюдается интерференционный минимум.

Для монохроматического света на экране будет ряд чередующихся темных и светлых полос. При белом свете на экране светлые полосы будут цветными (за исключением центральной для), которые своим фиолетовым краем обращены к центру интерференционной картины.

В природе часто можно наблюдать радужное окрашивание тонких пленок (масляные пленки на воде, мыльные пузыри, оксидные пленки на металлах), возникающее в результате интерференции света, отраженного двумя поверхностями пленки. Если пленка имеет переменную толщину, то на её поверхности наблюдается полосы, отмечающие участки с постоянной толщиной, которые называются полосами равной толщины. Полосы равной толщины наблюдаются у поверхности пленки, поскольку лучи из такой пленки выходят под разными углами и пересекаются непосредственно у поверхности. Соседние полосы соответствуют толщинам, отличающиеся друг от друга на величину порядка . Поэтому, подсчитав число полос равной толщины, можно определить изменение толщины пленки, вычислить размеры неровностей. Если неровность имеет форму впадины или выпуклости, то полосы равной толщины имеют форму колец, а если пленка имеет форму клина, то они будут параллельными прямыми. Такие полосы можно наблюдать на вертикальных мыльных пленках, на пленках нефти и масла, разлитых по воде. Если свет не монохроматический, то полосы будут цветными.

Впервые полосы равной толщины от клина были описаны Ньютоном. Плосковыпуклая линза очень большого радиуса кривизны прижимается выпуклой стороной к плоской пластине так, чтобы между ними образовался воздушный зазор переменной толщины – воздушный клин (рис. 5). Роль тонкой пленки, от поверхностей которой отражаются когерентные волны, играет воздушный зазор между пластиной и линзой. При нормальном падении света полосы равной толщины имеют вид концентрических окружностей.

В отраженном свете оптическая разность хода (с учетом потери полуволны при отражении и для )

,,

где – ширина зазора.

Как видно из рисунка 5,

,

,

где - радиус кривизны линзы,радиус кольца.

Т.к. ,.

При наблюдении максимума , поэтому радиус светлого кольца определяется формулой

.

При наблюдении минимума , радиус темного кольца определяется формулой

.

При наблюдении в проходящем свете эти выражения для ивзаимно меняются.

Применение интерференции:

а) для измерения длин световых волн (измеряя радиусы колец Ньютона);

б) явление интерференции лежит в основе просветления оптики;

в) явление интерференции положено в основу метода контроля качества изготовления поверхностей зеркал, линз, призм и т.д.; так, например, симметричность и правильность колец Ньютона свидетельствует о высокой точности изготовления и шлифовки линз;

г) для создания самолетов – "невидимок";

д) для создания высокоотражающих покрытий на основе многолучевой интерференции.