Уравнения равномерного вращения тела

Вращение тела с постоянной угловой скоростью называется равномерным

Проинтегрируем

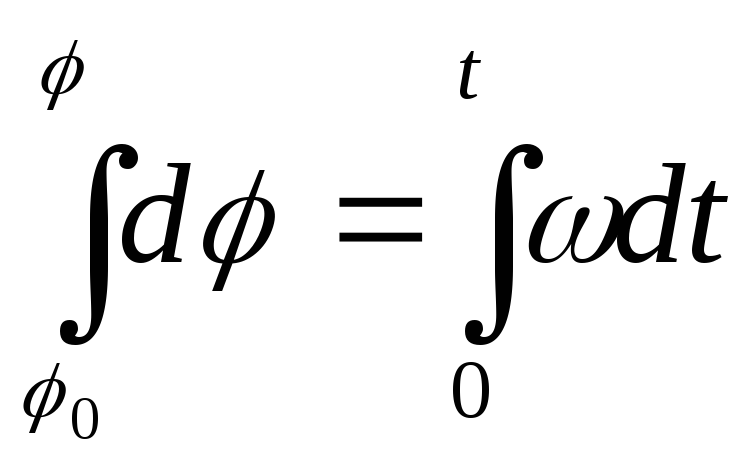
–уравнение равномерного вращения тела.

Уравнения равнопеременного вращения тела

Вращение тела, при котором угловое ускорение постоянно, называется равнопеременным вращением.

Если величина увеличивается, то вращение называется равноускоренным, если уменьшается – равнозамедленным.

Разделим переменные:

Проинтегрируем:

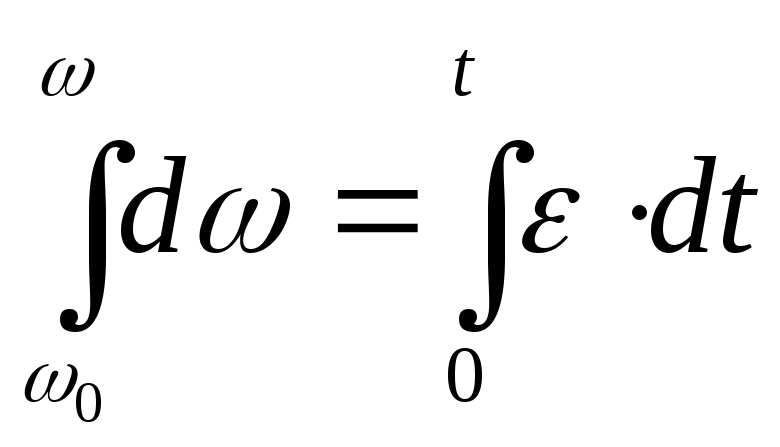
Разделим переменные:

Проинтегрируем:

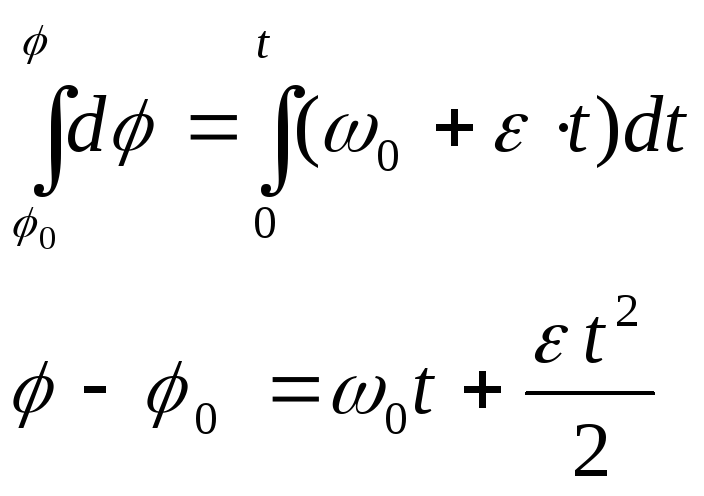
В результате получим:

В общем случае:

–уравнение равнопеременного движения.

Знак «+» – соответствует ускоренному вращению,

«–» – замедленному.

3.2.1. Скорость и ускорение точки твердого тела, вращающегося вокруг неподвижной оси.

Р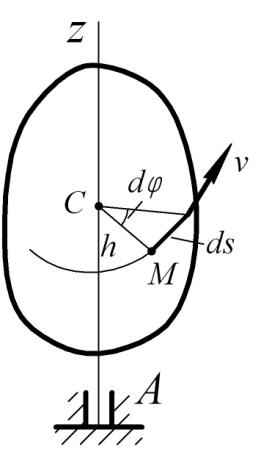ассмотрим точку М, находящуюся на расстоянииh от оси вращения Аz.

При вращении точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна к оси вращения, а центр С лежит на самой оси. Если за время происходит элементарный поворот тела на угол, то точка М при этом совершит вдоль своей траектории элементарное перемещение. Тогда скорость точки будет равна

_{Рис. 2.10} или ₍₂₁₎

Скорость называют еще линейной или окружной скоростью точки М.

Направлена линейная скорость по касательной к описываемой точкой М окружности.

Как следует из формулы, линейные скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения.

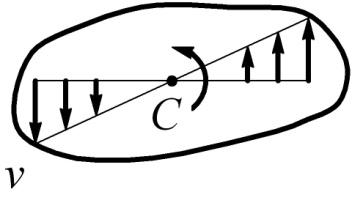
Рис. 2.11

Для нахождения ускорения точки М воспользуемся формулами:

В нашем случае . Подставляя сюда значение, получим:

или окончательно

К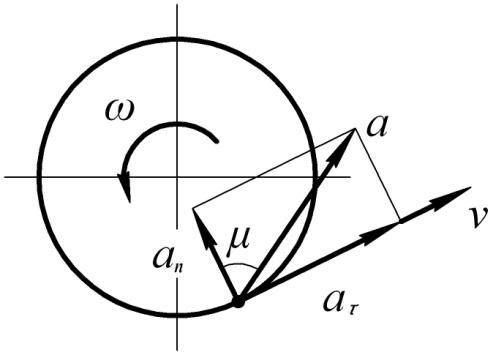асательное ускорениенаправлено по касательной к траектории (в сторону движения, если тело вращается ускоренно или в обратную, если тело вращается замедленно); нормальноевсегда направлено по радиусуh к оси вращения.

Рис. 2.12

Полное ускорение точки М будет равно

или

₍₂₃₎

Отклонение вектора полного ускорения от радиуса описываемой точкой окружности определяется углом , который вычисляется по формуле

Подставляя сюда значения и, получаем:

4. Сложное движение точки.

4.1. Основные понятия.

Сложное движение называется движение точки относительно двух систем отсчета, одна из которых неподвижна, другая произвольно перемещается относительно неподвижной системы координат.

Д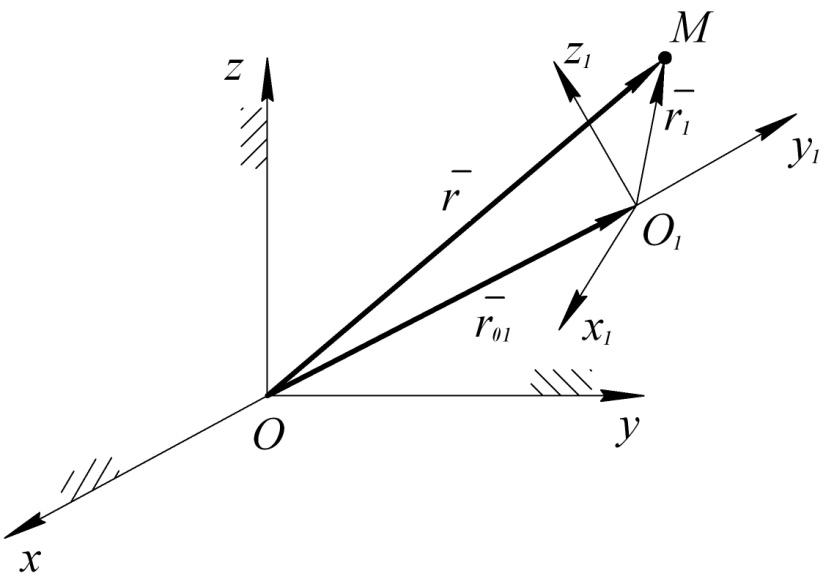вижение тоски М относительно неподвижной системы координат (О, х₁, у₁, z₁) называется абсолютным. Скорость и ускорение в этом движении называются абсолютной скоростью и абсолютным ускорением, обозначаются .

Движение точки М относительно подвижной

Рис. 2.13 системы координат (О, х, у,

z), называется относительным. Скорость и ускорение в этом движении называются относительной скоростью и относительным ускорением, обозначаются .

Подвижная система координат и все, что с ней неразрывно связано, называется переносной средой.

Движение точки М вместе с подвижной системой координат относительно неподвижной называется переносным движением. Скорость (ускорение) той точки переносной среды, с которой в данный момент времени совпадает наша точка, называются переносной скоростью (ускорением), обозначаются .

Примером может служить движение человека по эскалатору. Движение эскалатора есть переносное движение, движение человека вниз или вверх по эскалатору есть относительное, а движение по отношению к неподвижным стенам – абсолютное.

Движение точки М по отношению к неподвижной системе отсчета, которое названо абсолютным, является сложным, состоящим из относительного и переносного движения точки. Основная задача изучения сложного движения состоит в установлении зависимостей между скоростями и ускорениями относительного, переносного и абсолютного движения точки.