3.1.2. Операторные реактивности синхронной машины

По аналогии с операторным сопротивлением операторная реактивностьявляется функцией, связывающей изображения для потокосцепления и тока.

О

(3.3)

ператорные реактивности машины без демпферных обмоток определяются на основе уравнений:

(3.4)

(3.5)

(3.6)

(3.7)

(3.8)

Из уравнения (3.7) можно выразить операторную реактивность поперечной оси:

Операторную реактивность в продольной оси находим, используя уравнения (3.5) и (3.6):

(3.9)

Второе слагаемое уравнения (3.9) не зависит от параметра и определяется только свойствами системы регулирования возбуждения. Поэтому операторная реактивность в продольной оси

.

Схемная интерпретация реактивности будет более наглядной, если выполнить ряд преобразований. Учитывая, что синхронная реактивность статора в продольной оси имеет две составляющие: реактивность рассеяния и реактивность взаимной индукции(для обмотки возбуждения), получим

(3.10)

Второе слагаемое представляет собой эквивалентное сопротивление двух параллельных ветвей .

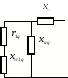
Аналогично можно определить операторные реактивности машины с демпферными обмотками. Схемы замещения, отвечающие этим реактивностям, приведены на рис. 3.1.

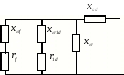
a

б

Рис. 3.1. Схемы замещения, определяющие операторные реактивности для машины с демпферными обмотками:

а - в продольной оси; б - в поперечной оси.

3.2. Внезапное короткое замыкание синхронной машины

При внезапном коротком замыкании синхронной машины система дифференциальных уравнений имеет вид

Использование численных методов интегрирования при их исследовании требует предварительного представления системы дифференциальных уравнений в виде задачи Коши, т.е. выполнения преобразований и вычисления начальных условий.

Алгоритм решения задачи следующий:

1. Определяют начальные условия на основе расчёта предшествующего режима синхронной машины.

2. Формируют систему дифференциальных уравнений вида

3. Выполняют интегрирование системы дифференциальных уравнений.

Кроме количественной оценки процесса короткого замыкания синхронной машины, можно рассмотреть качественное решение этих дифференциальных уравнений, используя их аналитические решения.

Для аналитического исследования необходимо использовать операторные уравнения, причём вместо полных переменных необходимо рассматривать их приращения, которые отвечают нулевым начальным условиям исходных дифференциальных уравнений.

Пусть машина не имеет демпферных обмоток и автоматического регулирования возбуждения (АРВ). Рассматривая внезапное короткое замыкание на шинах генератора, можно считать, что .

Система операторных уравнений имеет вид:

В случае несимметричного режима необходимо рассмотреть уравнение для нулевой составляющей

Искомый режим короткого замыкания может быть получен в результате наложения переходного режима на предшествующий стационарный режим, характеризуемый в момент коммутации параметрами . Причём переходный режим развивается с нулевых начальных условий и обусловлен приращениями напряженийв месте короткого замыкания. Таким образом, с учётомимеем

(3.11)

Задача сводится к решению алгебраических уравнений относительно тока в статоре – с последующим переходом от изображений к оригиналу.

Из системы уравнений (3.11) получаем

Для перехода к оригиналу используем выражение

Знаменатель имеет 4 корня: один нулевой, два комплексных сопряжённых, один вещественный. Если принять , то в аналитической форме можно записать:

Используя теорему разложения, можно построить оригиналы , а затем полные значения фазных токов, например для фазы А:

Здесь

Третья составляющая определяет вторую гармонику и обусловлена несимметрией ротора (). Физически вторая гармоника статора связана с пульсирующей составляющей поля ротора, созданного апериодическими составляющими тока статора.

В случае машины без демпферных обмоток, но с АРВ уравнение баланса напряжений в обмотке возбуждения имеет вид:

Решение задачи аналогично предыдущему случаю. Однако полином в знаменателе имеет 6 корней, два из которых нулевые.

Учёт демпферных обмоток при решении задач о внезапном коротком замыкании синхронной машины может быть выполнен в общем виде только приближённо, как учёт влияния короткозамкнутых контуров.

Полученные решения применимы и для анализа процессов при коротком замыкании во внешней цепи, если под понимать значения напряжений в этой точке в предыдущем режиме, а все реактивности машины и активное сопротивление статора увеличить на , характеризующие цепь между статором и точкой короткого замыкания.