8. Однократная продольная несимметрия

Продольную несимметрию в какой-либо точке системы можно представить в общем виде включением в рассечку каждой фазы неодинаковых сопротивлений, причем последние могут быть еще связаны между собой взаимоиндукцией, значения которой для каждой пары фаз также различны.

Как отмечалось ранее, такой подход к решению задачи принципиально позволяет получить расчетные выражения для определения токов и напряжений в самом общем виде. Однако значительно проще и нагляднее проводить решение для каждого вида продольной несимметрии, используя характеризующие его граничные условия.

При этом, рассматривая только основную гармонику режима, исходят из следующих условий: включение сопротивления в фазу при неизменной ЭДС источника питания тождественно шунтированию таких же сопротивлений в других фазах, шунтирование в фазе тождественно включению такого же сопротивления, но с обратным знаком, разрыв фазы тождественен включению в место разрыва источника напряжения, равного падениюнапряжения на концах разорванной фазы.

Как и для поперечной несимметрии, при расчете продольной несимметрии эффективным является применение метода симметричных составляющих, в соответствии с которым расчетные выражения можно выразить через симметричные составляющие тока и напряжения фазы «А», принятой за основную (особую).

(8.1)

(8.2)

где – токи и падения напряжения для несимметричной системы фазных величин А, В и С;

–симметричные составляющие токов и падений напряжения прямой, обратной и нулевой последовательностей.

Токи определенных последовательностей вызывают падения напряжения соответствующих последовательностей. Эта взаимосвязь их описывается системой независимых уравнений

(8.3)

где – суммарная ЭДС источников питания, имеющая место только в схеме прямой последовательности;– результирующие сопротивления отдельных последовательностей относительно места нарушения продольной несимметрии.

Таким образом, как и при поперечной несимметрии, методика получения расчетных соотношений основывается на решении системы уравнений (8.1) – (8.3) с учетом граничных условий, характеризующих несимметрию.

В настоящем разделе рассмотрены два вида наиболее часто встречающейся продольной несимметрии: разрыв одной фазы и разрыв двух фаз (в одном и том же месте).

Реальная схема с однократной продольной несимметрией приводится к схемам замещения без разрыва. Это достигается введением в месте повреждения источника продольного напряжения, имеющего значение, равное падению напряжения в месте продольной несимметрии.

В электрической системе могут возникать одновременно поперечная и продольная несимметрии в разных комбинациях, которые приводят к сложным видам повреждений. В этом случае последовательность вычислительных операций повторяется в каждой точке несимметрии.

8.1. Разрыв одной фазы трехфазной цепи.

Разрыв одной фазы можно характеризовать граничными условиями

(8.4)

(8.5)

, (8.6)

т.е. они аналогичны граничным условиям двухфазного короткого замыкания на землю.

При разложении на симметричные составляющие условия (8.5) и (8.6) приводят к равенствам

(8.7)

Используя (8.3) и (8.7), выразим как

(8.8)

, (8.9)

После подстановки (8.8) и (8.9) в (8.4) имеем

. (8.10)

где

. (8.11)

Для тока прямой последовательности фазы «А» в месте разрыва с учетом (8.3) и (8.10) получим

. (8.12)

Полученные аналогично приведены в таблице 8.1.

Для определения напряжений с одной стороны продольной симметрии следует предварительно найти по схемам отдельных последовательностей симметричной части цепи соответствующие составляющие этих напряжений. Прибавив к последним , находят симметричные составляющие напряжений с другой стороны продольной несимметрии. Зная симметричные составляющие токов и напряжений (табл. 8.1), можно, используя выражения (8.1) и (8.2), получить фазные величины токов и напряжений.

Необходимо отметить, что исходные уравнения, используемые при выводе выражений для расчетов токов и напряжений при разрыве одной фазы абсолютно аналогичны таковым для случая двухфазного короткого замыкания. Поэтому расчетные формулы, полученные там, могут быть использованы для расчетов токов, нахождения модуля фазных токов при анализе обрыва одной фазы.

Для иллюстрации на рис. 8.1,б,в,г приведены векторные диаграммы токов и напряжений в месте обрыва одной фазы «А».

в

б

г

а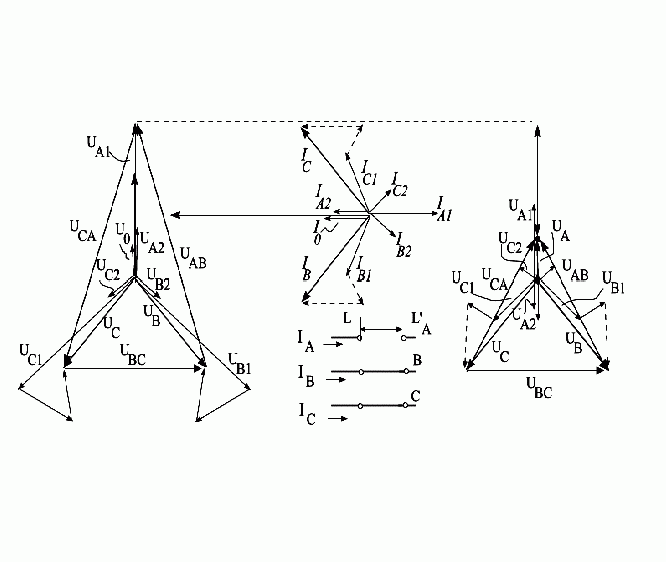

Рис.8.1. Разрыв одной фазы трехфазной цепи: а – исходная схема, б – векторная диаграмма токов в месте разрыва чисто индуктивной цепи, в и г – векторные диаграммы напряжений по концам разрыва (соответственно в точках L и L’).