7.3. Двухфазное короткое замыкание на землю

Двухфазное короткое замыкание на землю характеризуется граничными условиями

, (7.23)

(7.24)

Учитывая (7.23), получаем , откуда ток прямой последовательности

. (7.25)

По условиям (7.24) и используя (7.3), имеем

. (7.26)

Используя последнее равенство и уравнения (7.1), получим

, (7.27)

. (7.28)

С учетом (7.27), (7.28) по (7.25), имеем

. (7.29)

Приравняв значение по (7.1) и (7.29) можно записать

. (7.30)

Далее, действуя аналогично пункту 7.2, можно получить уравнения для вычисления фазных токов и напряжений, коэффициент взаимосвязи токов и ток в земле. Полученные результаты приведены в таблице 7.1.

Векторные диаграммы напряжений и токов в месте двухфазного короткого замыка­ния на землю изображены на рис. 7.3,б,в. Угол между токами поврежденных фаз может изменяться в пределах, стремясь к ниж­нему пределу прии к верхнему пределу при, что соответствует условиям двухфазного короткого замыкания без соединения с землей.

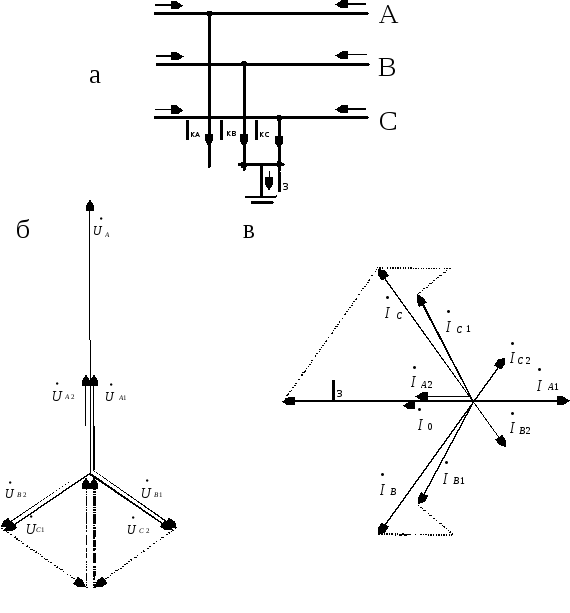
Рис. 7.3. Двухфазное короткое замыкание на землю: а – принципиальная схема, б – векторная диаграмма в месте короткого замыкания, в – то же для токов

4. Учет переходного сопротивления в месте замыкания

При коротких замыканиях переходное сопротивление в основном опре­деляется сопротивлением электрической дуги, которое в первом прибли­жении можно считать активным сопротивлением .

На рис. 7.4 приведены схемы несимметричных коротких замыканий с учетом сопротивления дуги. Здесь двухфазное короткое замыкание через дугу представлено как глухое короткое замыкание на ответвлении, фазы которого имеют одинаковое сопротивление . В схему однофазного короткого замыкания в каждую фазу введены одинаковые сопротивления. Такие искусственные приемы не нарушают граничных условий и позволяют наиболее просто получить расчетные формулы для токов и напряжений последовательностей и действительных токов и напряжений фаз по аналогии с формулами (табл. 7.1).

Для однофазного короткого замыкания через дугу формула для определения тока прямой последовательности имеет вид

(7.31)

для двухфазного короткого замыкания:

(7.32)

для двухфазного короткого замыкания на землю:

(7.33)

Рис. 7.4. Схемы несимметричных коротких замыканий через дугу для двухфазного (а), однофазного (б), двухфазного на землю (в) замыканий

4. Правило эквивалентности прямой последовательности

Структура выражений (7.8), (7.22) и (7.30) позволяет в общем виде записать ток прямой последовательности фазы «А» при любом несимметричном коротком замыкании через параметры цепи:

(7.34)

где (n) - обозначает вид короткого замыкания; - дополнительное сопротивление в зависимости от вида короткого замыкания (табл. 7.1).

С учетом того, что фазные токи в месте короткого замыкания пропорциональны току прямой последовательности, модуль фазного тока в месте короткого несимметричного короткого замыкания определяется выражением

(7.35)

где m⁽ⁿ⁾ – по данным таблицы 7.1.

Обобщенная запись выражения (7.35) позволила Н. Н. Щедрину сформулировать следующее весьма важное положение.

Ток прямой последовательности любого несимметричного короткого замыкания может быть определен как ток при трехфазном коротком замыкании в точке, удаленной от действительной точки короткого замыкания на дополнительное сопротивление , которое не зависит от параметров схемы прямой последовательности и для каждого вида короткого замыкания определяется результирующими сопротивлениями обратной и нулевой последовательностей относительно рассматриваемой точки схемы, а также в общем случае сопротивлением возникшей дуги.

Это положение, которое называют правилом эквивалентности прямой последовательности, справедливо при условии, что рассматривается только основная гармоника несимметричного тока короткого замыкания.

Установленная идентичность между токами прямой последовательности несимметричного короткого замыкания и токами при некотором эквивалентном трехфазном коротком замыкании подтверждает то, что все полученные ранее выражения тока трехфазного короткого замыкания можно распространить на случай несимметричных коротких замыканий.

Правило эквивалентности прямой последовательности и установленные значения x_Δ⁽ⁿ⁾ m⁽ⁿ⁾ (см. табл. 7.1) позволяют достаточно просто сравнить различные виды короткого замыкания. Ограничимся таким сравнением для условий, когда короткозамкнутая цепь чисто индуктивная.

Полагая, что короткие замыкания различных видов происходят поочередно в одной и той же точке системы и при одних и тех же исходных условиях на основании данных таблицы 7.1 можно записать следующие неравенства:

Выясним пределы, в которых могут находиться значения токов при несимметричных коротких замыканиях по сравнению со значениями токов трехфазного короткого замыкания, возникающего в той же точке системы. Знание этих пределов представляет практический интерес, так как позволяет по известному значению тока трехфазного короткого замыкания оценить в первом приближении возможные наибольшие и наименьшие значения тока при несимметричных КЗ.

Например, при двухфазном коротком замыкании:

При КЗ вблизи зажимов генератора x_вн ≈0. При этом в начальный момент КЗ (t=0) x_1r =x_d x_2r ≈x_d. Следовательно,

X_1рез ≈ x_2рез; .

В установившемся режиме (t=∞), при котором X_1р=x_d; X_2р<<x_d; X_1рез>>x_2рез,можно полагать X_2рез≈0. Тогда Следовательно, отношениеK_(2-3) находится в следующих пределах:

Таблица 7.1. Симметричные составляющие токов и напряжений в месте коротких замыканий

№ пп	Наименование и обозначение величин	Вид короткого замыкания
		Трехфазное	Двухфазное	Однофазное	Двухфазное на землю
1	2	3	4	5	6
1	Ток прямой последовательности IA1
2	Ток обратной последовательности IA2	0	- IA1	IA1
3	Ток нулевой последовательности I0	0	0	IA1
4	Полный ток фазы: IA IВ IС	Iа1 Iа1 Iа1	0	3 IA1 0 0	0
5	Напряжение прямой последовательности UА1	0
6	Напряжение обратной последовательности UА2	0	UА1		UА1

Продолжение таблицы 7.1

1	2	3	4	5	6
7	Напряжение нулевой последовательности UА0	0	0		UА1
8	Полное фазное напряжение: UА UВ UС	0 0 0	2 UА1 UА1 UА1	0	3 UА1 0 0

Примечание. а = - 0,5 + j 0,866, а² = - 0,5 – j 0,866, а – а² = j , а² – а = - j .

Таблица 7.2. Значения дополнительного сопротивления и коэффициентаm⁽ⁿ⁾

Вид замыкания	(n)		m(n)
Трехфазное	(3)	0	1
Двухфазное	(2)
Однофазное	(1)		3
Двухфазное на землю	(1,1)
То же при	(1,1)

Примечание. Для упрощения записи опущен индекс у величин, которые являются соответствующими результирующими сопротивлениями относительно места короткого замыкания.

Важно заметить, что величина тока прямой последовательности в месте короткого замыкания, а также связанные с ней величины токов других последовательностей зависят от сопротивлений всех последователь­ностей элементов рассматриваемой схемы (включая сопротивление дуги при ее учете). Так, например, если нейтраль трансформатора, на выводах которого имеется однофазное или двухфазное короткое замыкание на землю, заземлить через какое-либо сопротивление, то это скажется на величинах токов всех последовательностей, хотя токи прямой и обратной последовательностей через это сопротивление и не протекают.