Сопромат / Руководство к практическим занятиям по сопротивлению материалов / Раздел_7

80

Тема практического занятия № 7: геометрические характеристики плоских поперечных сечений стержня

7.1. Краткие сведения из теории

Рассмотрим плоскую фигуру произвольной формы, являющуюся поперечным сечением стержня (рис. 7.1).

Рис. 7.1

Площадь фигуры внутри контура является ее первой геометрической характеристикой. Отнесем фигуру к осям и рассмотрим интегралы

, (7.1)

. (7.2)

Величины (7.1) называются статистическими моментами площади сечения относительно осей и , а величины (7.2) – моментами инерции этой же площади соответственно. Два первых момента инерции − осевые моменты инерции, а – центробежный. Сумма осевых моментов инерции представляет собой полярный момент инерции

,

так как .

Радиусами инерции сечения называют положительные величины

.

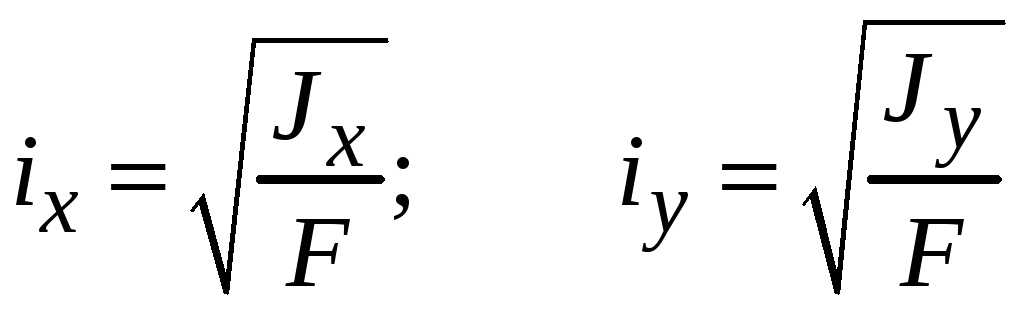Геометрические моменты сопротивления сечения относительно осей и − это величины

.

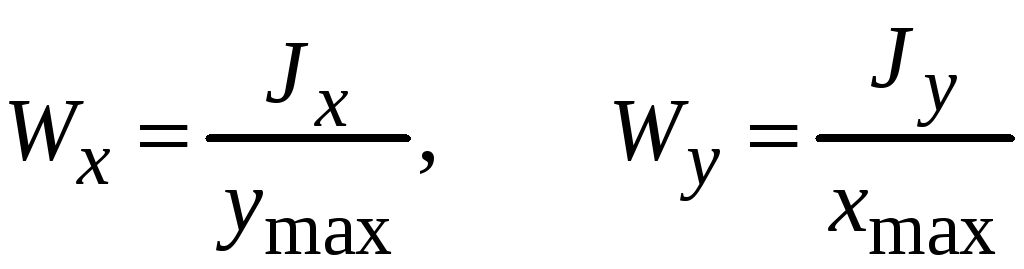Проведем вспомогательные оси и , параллельные осям и . Тогда координаты произвольной точки в новой системе координат определяются формулами

,

где – координаты начала старой системы координат относительно новой Статические моменты в новой системе

. (7.3)

Центральными осями называют такие оси, относительно которых статические моменты равны нулю: . Точка пересечения центральных осей − это центр тяжести. Обозначим координаты центра тяжести: . Тогда из уравнений (7.3) получим

.

Моменты инерции при параллельном переносе осей относительно центральных осей и

. (7.4)

При повороте центральных осей и в новое положение и на угол они преобразуются по формулам

.

В результате получаем

(7.5)

Главными осями инерции поперечного сечения называют такие оси, относительно которых осевые моменты инерции принимают экстремальные значения

. (7.6)

Значения осевых моментов инерции называются главными.

Направление главных осей характеризуется углами , которые определяются по формуле

. (7.7)

Главные оси обозначаются цифрами и 2, а главные моменты инерции . Центробежный момент инерции относительно главных осей равен нулю. Любая ось геометрической симметрии является главной.

Все расчетные формулы сопротивления материалов выводятся по отношению к главным центральным осям инерции поперечного сечения стержня.

7.2. Порядок определения геометрических характеристик для сложных сечений

Рассмотрим произвольное поперечное сечение (рис. 7.2).

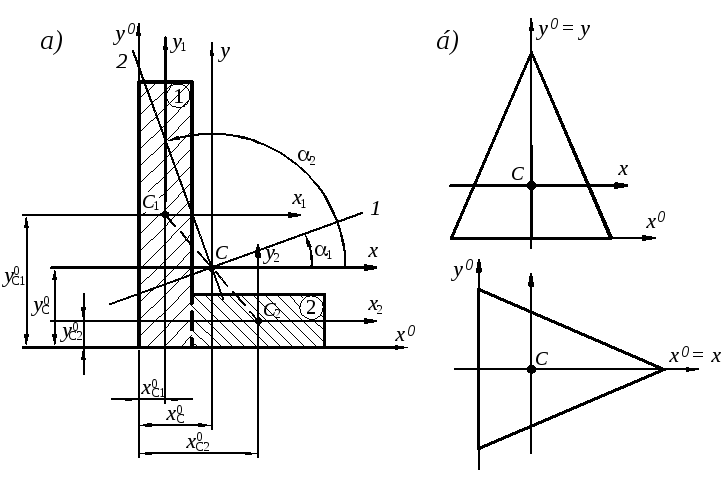
Рис. 7.2

1. Проводятся вспомогательные оси 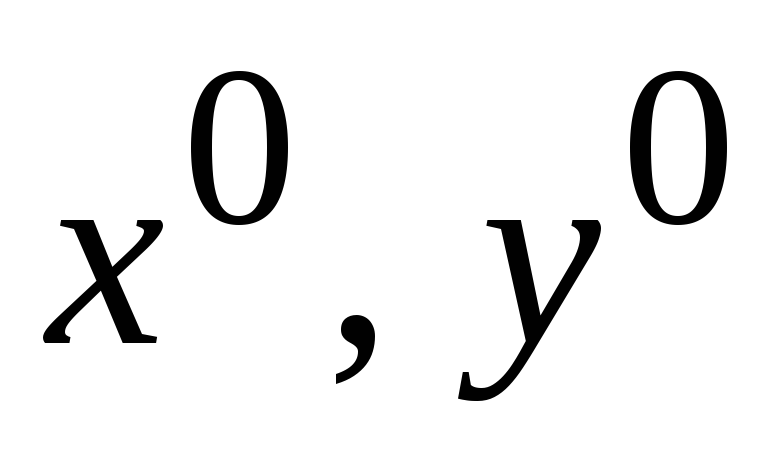так, чтобы вся несимметричная фигура располагалась в первой четверти (рис. 7.2а), если имеется ось симметрии, то она выбирается за или 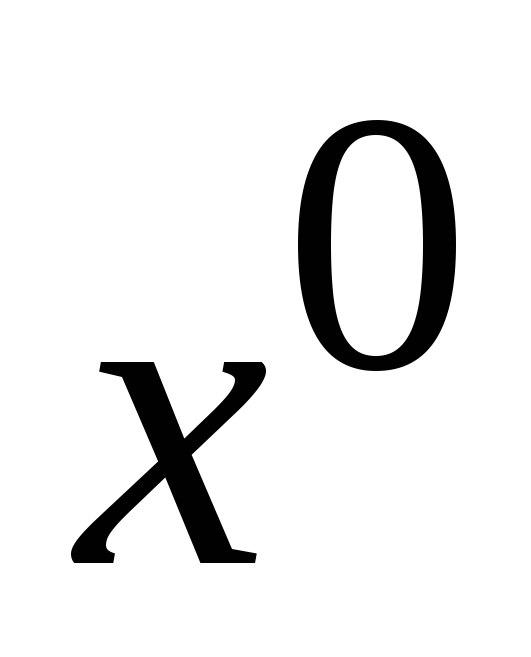(рис. 7.2б).

2. Сложная фигура разбивается на простейшие с легко определяемыми центрами их тяжести , через которые проводим центральные оси , параллельные вспомогательным осям .

3. Определяем геометрические характеристики простых фигур относительно своих центральных осей, т.е.

.

4. Определяем координаты центра тяжести всей сложной фигуры во вспомогательных осях по формулам

, .

Проводим через центр тяжести центральные оси , параллельные вспомогательным осям .

5. Вычисляем моменты инерции всего сечения относительно центральных осей по формулам

, , , (7.8)

где , .

6. Определяем направления главных центральных осей, используя формулу

(7.9)

7. Определяем главные моменты инерции относительно главных центральных осей по формуле

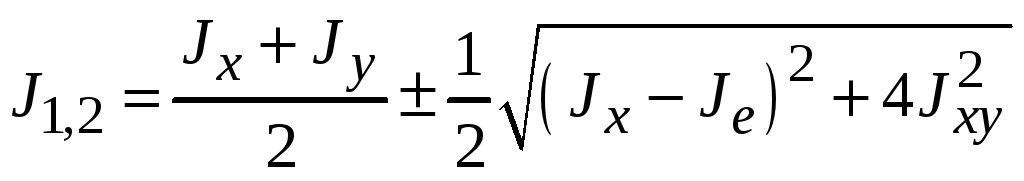, (7.10)

где , .

8. Делаем проверку правильности вычисленных главных моментов инерции по формуле

(7.11)

7.3. Примеры решения задач

№1. Для прямоугольного поперечного сечения определить моменты инерции относительно осей геометрической симметрии и осей совпадающих со сторонами прямоугольника (рис. 7.3).

Рис. 7.3

Решение

Оси являются главными центральными для прямоугольного поперечного сечения, так как они совпадают с осями геометрической симметрии. Оси − в данном случае будут вспомогательными. Для определения осевого момента инерции выделим на расстоянии полоску шириной и толщиной , следовательно , тогда

Теперь рассмотрим на расстоянии от оси полоску шириной и толщиной , в этом случае и момент инерции будет равен

Центробежный момент инерции

где .

Моменты инерции относительно осей , можно вычислить используя формулы переноса (7.5), полагая , тогда

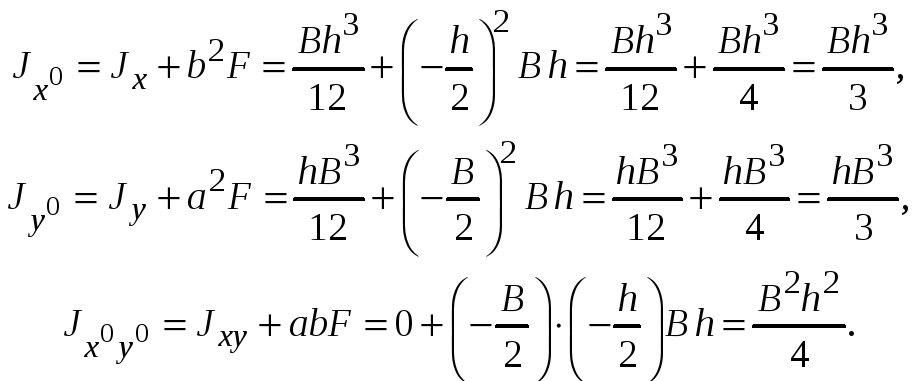
№2. Определить геометрические характеристики относительно центральных и главных осей для сечения в виде прямоугольного треугольника, изображенного на рис. 7.4.

Рис. 7.4

Решение

Отнесем треугольник к вспомогательной системе координат В качестве элементарной площади возьмем полоску на расстоянии толщиной и переменной ширины так, что

.

Из подобия треугольников нетрудно установить, что:

,

тогда .

Статический момент будет равен

По аналогии получим

Площадь треугольника

.

Координаты центра тяжести определим по формулам:

Через точку проводим центральные оси параллельные осям

Момент инерции и аналогично равны:

,

.

Для определения момента инерции относительно центральной оси x воспользуемся формулой (7.5) при параллельном переносе осей

.

Так как , то

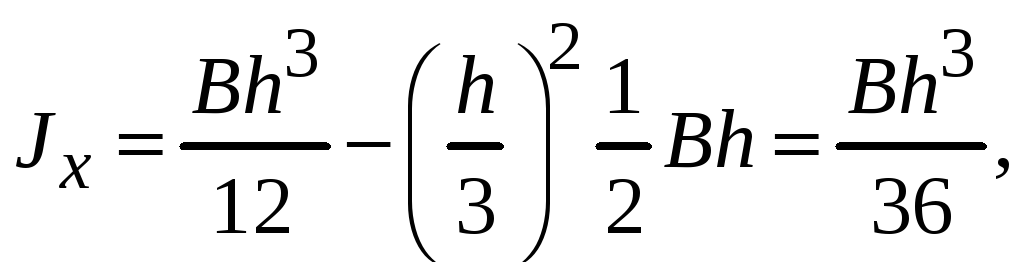
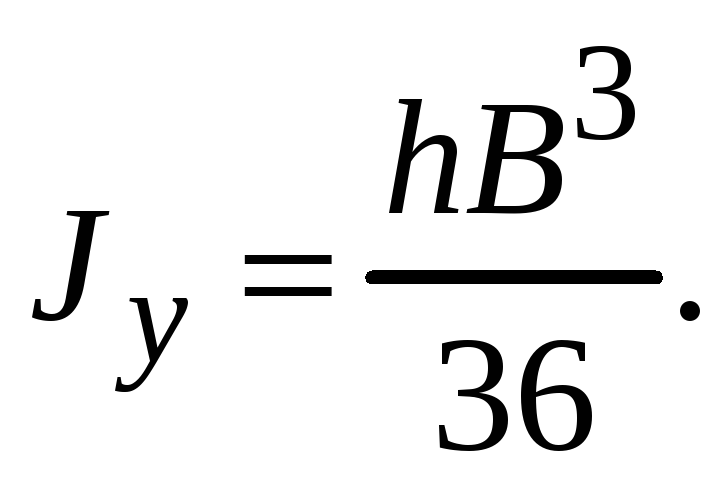
Центробежный момент

,

где ; .

Интегрируя, получаем

Перейдя к центральным осям и , получим

.

Для определения направлений главных осей используем формулу (7.7):

.

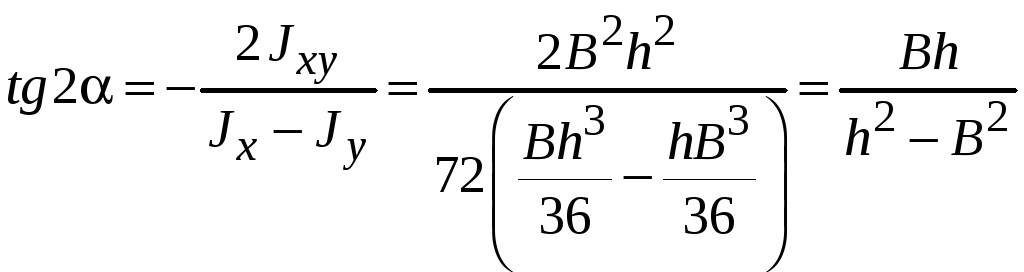Проводим главные центральные оси 1 и 2.

Если, например, , то имеем равнобедренный треугольник, для которого , , . По формуле (7.6) вычисляем главные моменты инерции:

.

№3. Определить площадь и моменты инерции относительно главных центральных осей инерции круглого поперечного сечения диаметра (рис. 7.5).

Рис. 7.5

Решение

Выберем оси , которые для круглого сечения будут главными и центральными, так как являются осями геометрической симметрии. В качестве элементарной площади возьмем полоску на уровне толщиной и шириной , т.е. . Координаты точки на контуре сечения, а также равны:

.

Тогда элементарная площадь

.

Площадь круга

.

Моменты инерции относительно оси

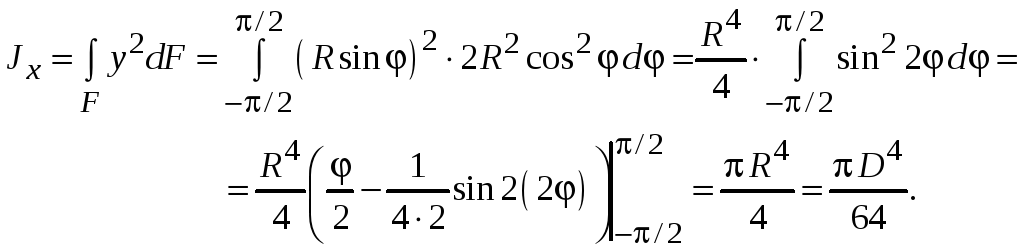
Такое значение имеет момент инерции относительно оси . Следовательно, полярный момент инерции для круга

.

№4. Определить положение центра тяжести и моменты инерции относительно главных центральных осей для поперечного сечения в виде полукруга (рис. 7.6).

Рис. 7.6

Решение

Проводим вспомогательные оси при этом учтем, что ось является осью геометрической симметрии и будет одной из главных центральных осей инерции сечения − 1 (см. рис. 7.6). Вторая главная центральная ось будет проходить через центр тяжести сечения и перпендикулярно оси .

Площадь полукруга .

Статический момент относительно вспомогательной оси равен

,

где смотри пример №3.

Координаты центра тяжести в осях :

Через точку С с координатами проводим вторую главную центральную ось инерции − 2 (см. рис. 7.6). Таким образом положение главных центральных осей для заданного сечения − определено.

Моменты инерции полукруга относительно осей будут равны половине моментов инерции полного круга, найденных в предыдущей задаче:

.

Определим осевые моменты инерции сечения относительно главных центральных осей

№5. Найти центробежный момент инерции для равнобокого уголка 125х125х10 (мм) относительно центральных осей .

Решение

Из таблицы ГОСТа для уголка (рис. 7.7а) находим .

Центробежный момент

.

Для уголка (рис. 7.7б) угол ,

.

Для уголка (рис. 7.7в) угол ,

.

Рис. 7.7

№6. Для симметричного сечения требуется определить моменты инерции, моменты сопротивления и радиусы инерции относительно главных центральных осей (рис. 7.8).

Решение

Представим сложное сплошное сечение, состоящее из трех простейших фигур: (полукруга 1, квадрата 2, треугольного выреза 3).

Отнесем фигуру к вспомогательным осям так, чтобы ось совпала с осью геометрической симметрии фигуры.

Укажем центры тяжести каждой фигуры , через которые проведем вспомогательные центральные координатные оси .

Рис. 7.8

Так как ось является осью симметрии данного сечения, положение его центра тяжести определяется одной координатой , вычисляемой по формуле

. (1)

Определяем площади и координаты центров тяжести отдельных фигур:

Подставляя полученные значения в формулу (1) для определения координаты , получим

Укажем на чертеже положение центра тяжести сечения с координатами и проводим через него центральные оси , параллельные вспомогательным осям .

Для контроля правильности определения положения центра тяжести найдем статический момент площади составного сечения относительно центральной оси :

,

где − координаты центров тяжести отдельных фигур.

Получим

Равенство свидетельствует о том, что координата центра тяжести определена верно.

Так как ось симметрии является не только центральной, но и главной, то центральные оси будут центральными главными осями инерции поперечного сечения 1, 2 .

Вычислим осевые моменты инерции составного сечения относительно главных центральных осей:

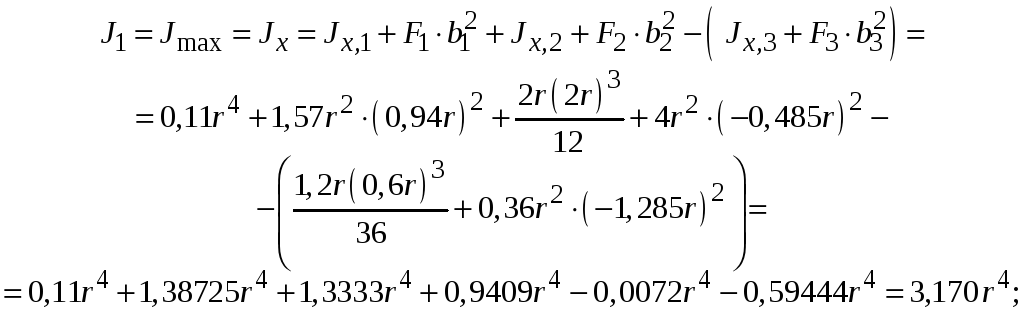
Непосредственно из чертежа определяем расстояния от наиболее удаленных точек сечения до главных центральных осей:

Вычислим моменты сопротивления составного сечения относительно главных центральных осей по формулам

Определим радиусы инерции

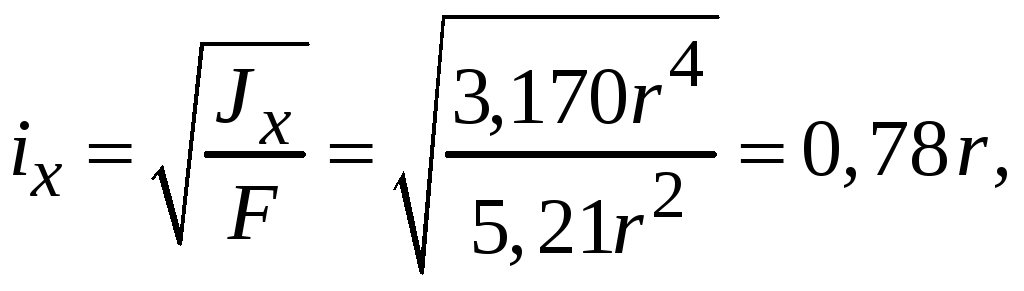
№7. Для составного сечения (рис. 7.9), состоящего из швеллера №18 и неравнополочного уголка 8х5х0,5 требуется: определить положение главных центральных осей сечения и вычислить главные центральные моменты инерции сечения.

Решение

Данная фигура сложная, не имеет осей геометрической симметрии. Выберем вспомогательные оси так, чтобы вся фигура располагалась по отношению к ним в первой четверти. Разбиваем сложное сечение на две простейшие − стандартные прокатные профили: 1 − швеллер №18 (рис. 7.10), 2 − неравнополочный уголок 8х5х0,5 (рис. 7.11).

Рис. 7.9

Из соответствующих таблиц сортамента определяем геометрические характеристики для швеллера №18 относительно своих центральных осей :

Рис. 7.10

Оси для швеллера являются не только центральными, но и главными осями инерции, так как одна из осей (ось ) − ось геометрической симметрии сечения, поэтому центробежный момент инерции .

Рис. 7.11