Сопромат / Руководство к практическим занятиям по сопротивлению материалов / Раздел_3
.doc
Тема практического занятия № 3: Статически неопределимые задачи при растяжении–сжатии стержней
3.1. Краткие сведения из теории
Статически неопределимыми задачами называют такие, в которых число неизвестных опорных реакций превышает число независимых уравнений статики. Разность между числом неизвестных реакций и числом независимых уравнений статики называется степенью статической неопределимости задачи, которая определяет «лишнее» число независимых реакций. Соответствующие лишним неизвестным простые связи называются лишними.
На рис. 3.1а
изображена заданная схема один раз
статически неопределимой задачи. Выберем
нижнюю опору в заданной схеме «лишней»
и отбросим ее. Схема или статически
определимая система, получается из
заданной путем отбрасывания лишней
связи, и называется основной
системой (рис.
3.1б).
Эквивалентной
называют
основную систему не только с приложенной
внешней нагрузкой, но и «лишней»
неизвестной
(рис.
3.1б).
Смысл эквивалентности систем заключается
в том, что перемещение сечения
отсутствует, т.е.
.
(3.1)
Рис. 3.1
Используя принцип независимости действия сил и закон Гука для эквивалентной системы, вместо (3.1) находим перемещение:
,
откуда
.
Из уравнения равновесия
находим реакцию
.
Статическая неопределимость задачи раскрыта. Изложенный метод решения статически неопределимых задач носит название метода сил, т. к. за основные неизвестные в этом методе приняты силы.
Усилия в стержнях находим с помощью метода сечения (рис. 3.1г):
,
.
Напряжения
,
.
Сопоставляя напряжения, устанавливаем
и требуем, чтобы
это напряжение не превосходило
допускаемого
.
3.2. Примеры решения задач
№1.
Определить
усилия и нормальные напряжения в стержне
с зазором
,
изображенном на рис. 3.2, при действии
силы
и нагревании на
.
Принять зазор
.
Рис. 3.2
Решение
В результате сборки
конструкции (ликвидации зазора
),
действии силы
и температуры
в опорах возникнут реакции
.
Уравнение равновесия имеет вид
.
(1)
Задача один раз
статически неопределима. Решаем задачу
методом сил. Для
эквивалентной системы составляем
дополнительное уравнение совместности
деформаций.
Перемещение сечения
ограничено, поэтому
.
Используя принцип независимости действия сил и закон Гука для эквивалентной системы получаем
,
или
,
откуда
.
(2)
Из уравнения (1) с учетом (2) получаем
.
Методом сечения находим усилия на каждом из участков стержня:
Напряжения
Таким образом,
каждое из слагаемых в выражениях для
напряжений содержит три вида слагаемых.
Первые возникают за счет действия силы
,
вторые – за счет изменения температуры
(температурные напряжения), третьи −
за счет устранения зазора δ (монтажные
напряжения).
В первом случае,
когда (
),
силовые напряжения
,
,
,
т.е. первый участок стержня растягивается, а второй сжимается.
Во втором случае,
когда действует только температура (
)
,
,
,
т.е. напряжения во всем стержне сжимающие.
В третьем случае
(
)
,
,
оба участка растянуты. В этом случае стержень был растянут для ликвидации зазора и закреплен.
№2.
Сила
передаётся через абсолютно жёсткую
плиту А
на сплошной стальной цилиндр 1
площадью поперечного сечения 15 см2
и полый медный цилиндр 2
площадью 20 см2.
Сила действует по оси обоих цилиндров
(рис. 3.3). Требуется: найти усилия в
стальном
и медном цилиндрах
;
изменить температуру конструкции, чтобы
усилия в стальном и медном цилиндрах
были одинаковы
;
изменить температуру конструкции, чтобы
напряжения в стальном и медном цилиндрах
были одинаковы
.
Принять: Р = 45 кН; F1 = 15 см2; F2 = 20 см2; E1 = 2∙105 МПа; E2 = 1∙105 МПа; коэффициент линейного расширения для стали 1 = 1,2∙10 -5 1/град, для меди 2 = 1,6∙10 -5 1/град.
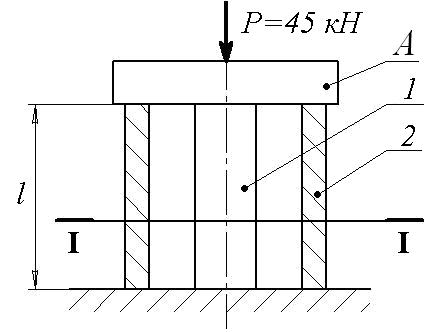
Рис. 3.3
Решение
-
Определение усили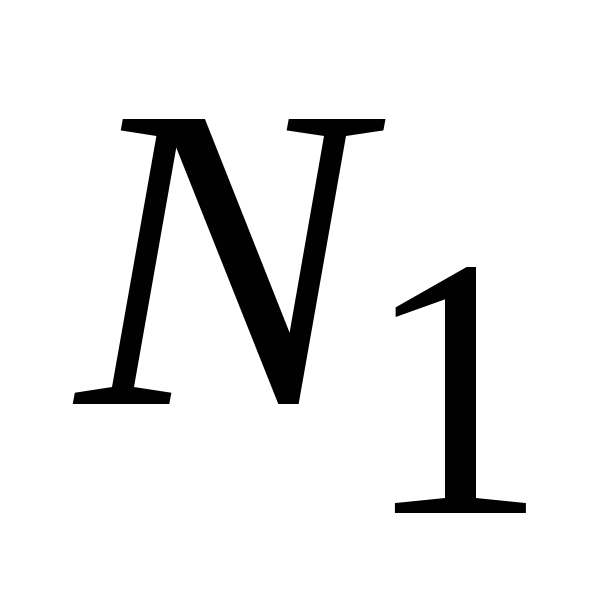й
и
Сделаем сечение
и рассмотрим равновесие верхней
отсечённой части, действие отброшенной
части заменим усилиями
и
(рис. 3.4).
Для данной системы сил можно составить одно уравнение статики. (У=1). Число неизвестных равно двум (R=2). Таким образом, система один раз статически неопределима:
.
Рис. 3.4
Составим уравнение равновесия
(1)
Рассмотрим систему в деформированном состоянии (рис. 3.5) и составим уравнение совместности перемещений.
Рис. 3.5
Очевидно, что
. (2)
Выразим деформацию цилиндров 1 и 2 через усилия
(3)
(4)
где учтено
.
Подставив (3) и (4) в (2), получим
(5)
Решаем совместно (1) и (5). Из уравнения (5) получим:
Подставляя
полученное выражение
в уравнение (1), получим
откуда
(6)
Тогда
(7)
Знак «минус» в выражениях (6) и (7) говорит о том, что усилия в цилиндрах будут сжимающими.
2. Изменение
температуры конструкции
,
чтобы усилия в цилиндрах стали одинаковыми
(
)
Из уравнения (1) имеем
.
В выражениях для деформаций цилиндров (3) и (4) нужно учесть влияние изменения температуры Т. Тогда
Уравнение (2) перепишем в виде
или
откуда
.
Таким образом, чтобы усилия в цилиндрах стали одинаковыми, конструкцию нужно нагреть на 9,4 С.
3. Изменение температуры конструкции (Т*), чтобы напряжения в цилиндрах стали одинаковыми (1 = 2)
Напряжения в цилиндрах равны
Тогда с учетом
получаем
(8)
С учётом (8) уравнение статики (1) примет вид
откуда
Выражения для деформаций каждого из цилиндров
(9)
(10)
Подставляя (9), (10) в (2), после преобразования получаем
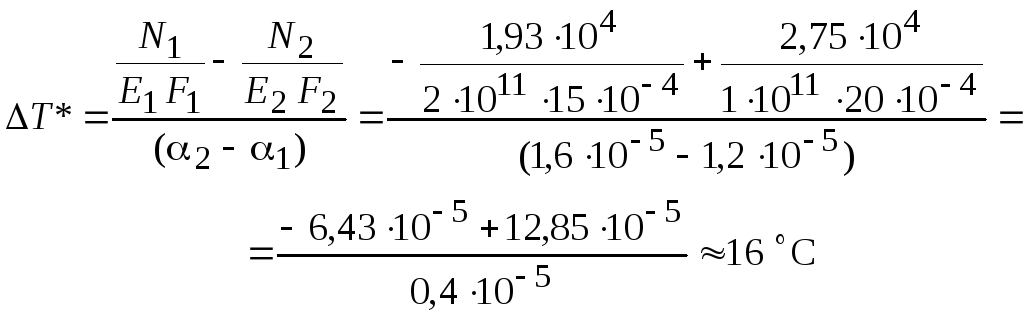
Таким образом, чтобы напряжения в стальном и медном цилиндрах стали одинаковыми, конструкцию нужно нагреть на 16 С.