Решение
Рассмотрим
равновесие узла А
после сборки конструкции (рис. 6.9). Получим
систему сходящихся сил на плоскости,
для которой можно составить два уравнение
статики. Число неизвестных − три (N1,
N2,
N3).
Таким образом, данная конструкция один
раз статически неопределима, т.е.
n
= R
− y
= 3 − 2 = 1.
Составим уравнение
статики
 (1)
(1)
 (2)
(2)
Из уравнения (2)
следует N1
= N3,
тогда уравнение (1) примет вид
N2
= −2N1cos.
(3)
Составим
дополнительное уравнение совместности
деформаций (удлинений стержней). Для
этого рассмотрим конструкцию в
деформированном состоянии (рис. 6.10).
|

|

|
|
Рис. 6.9
|
Рис. 6.10
|
Из АА1А2
имеем
 .
(4)
.
(4)
Выразим отрезки
АА1
и АА2
через деформации стержней:
АА1
= l2,
АА2
= l1.
Уравнение (4) запишем
в виде
l1
= l2
cos.
(5)
Выразим деформации
в стержнях 1 и 2 через усилия в стержнях,
при этом учтём, что второй стержень
выполнен короче заданного размера на
величину .
 (6)
(6)
 (7)
(7)
Выражения (6) и (7)
подставим в (5), и получим
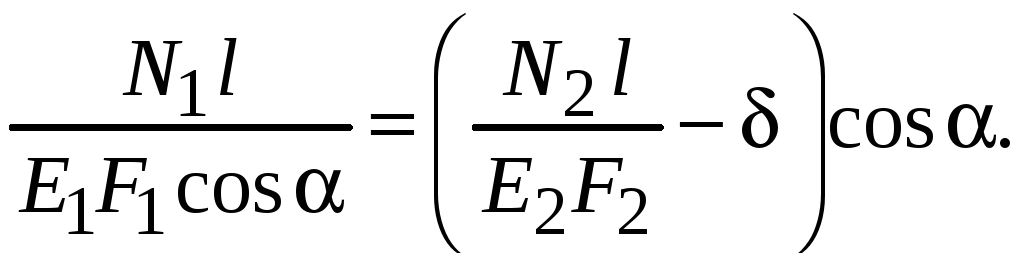 (8)
(8)
Учитывая, что
согласно (3) N2
= -2N1cos,
выражение (8) запишем
в виде

 (9)
(9)
Примем
= 45;
 = 1 м,
тогда из (9) имеем
= 1 м,
тогда из (9) имеем
 N2
= −2N1cos
= -2(-271)∙0,707 = 383,2 кН.
N2
= −2N1cos
= -2(-271)∙0,707 = 383,2 кН.
Таким образом,
статическая неопределимость задачи
раскрыта.
Определим напряжения
в стержнях


Вычисленные в
задаче усилия и напряжения называют
монтажными
или сборочными.




 (6)
(6) (7)
(7)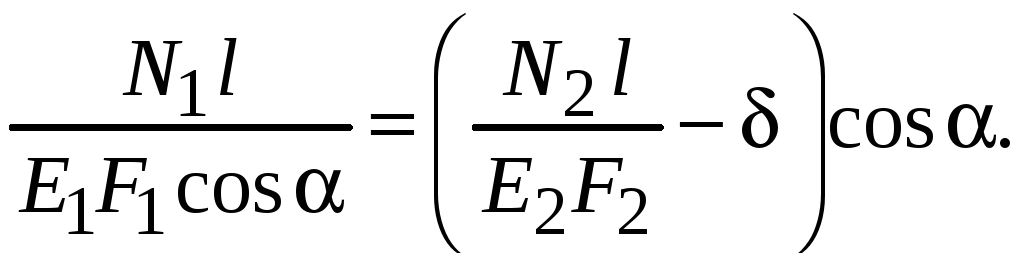 (8)
(8)
 (9)
(9) N2
= −2N1cos
= -2(-271)∙0,707 = 383,2 кН.
N2
= −2N1cos
= -2(-271)∙0,707 = 383,2 кН.
