Сопромат / Руководство к практическим занятиям по сопротивлению материалов / Раздел_10
.doc
Тема практического занятия № 10: сложный изгиб и Внецентренное растяжение – сжатие стержня
10.1. Краткие сведения из теории
Если брус подвергается одновременному действию косого изгиба и растяжения, то его сопротивление называют сложным.
В этом случае нормальное напряжение
.
(10.1)
Рис. 10.1
В частном случае
внецентренного растяжения (рис.10.1) точка
приложения растягивающей силы P
с координатами
не совпадает с центром тяжести сечения.
В этом случае
и формула (10.1) принимает вид
,
(10.2)
где принято
В отличие от косого
изгиба нейтральная линия
,
на которой
,
не проходит через центр тяжести. Ее
уравнение
,
или
,
где
–
отрезки, отсекаемые
нейтральной линией на осях
.
В наиболее удаленных точках A и B от нейтральной оси в поперечном сечении возникают максимальное и минимальное напряжения (рис. 10.2).
Рис. 10.2
Для этих точек составляем условие прочности
(10.5)
В окрестности центра тяжести C сечения существует область, называемая ядром сечения. Если приложить силу P внутри или на границе ядра сечения, то во всем сечении напряжения будут одного знака. Когда точка P находится на границе ядра сечения, то нейтральная линия касается контура сечения. Если катить эту касательную вдоль контура, то точка P приложения силы P вычертит границу ядра сечения.
10.2. Примеры решения задач
№1. В точке P колонны прямоугольного сечения приложена сжимающая сила P (рис. 10.3). Определить максимальное и минимальное нормальные напряжения.
|
|
|
Рис. 10.3 |
Нормальное напряжение при внецентренном сжатии определяем по формуле (10.1):
В нашей задаче
Момент инерции
,
площадь
,
следовательно
На нейтральной
линии
.
Поэтому ее уравнение
Наиболее удаленными точками от нейтральной оси являются точки A и B:
в точке A
и
в точке B
и
Если материал сопротивляется растяжению и сжатию различно, то следует составить два уравнения прочности:
№3.
Бетонный брус прямоугольного поперечного
сечения (рис. 10.5) нагружен продольной
силой
,
приложенной в точке
.
Требуется:
1) проверить
прочность бруса, если допускаемое
напряжение для бетона на растяжение
и
на сжатие
;
2) построить эпюру нормальных напряжений
в аксонометрии.
|
Рис. 10.5 |
Решение
1.
В данном случае нагружения брус будет
испытывать внецентренное растяжение-сжатие,
так как линия действия силы
где
|
параллельна продольной оси
,
но точка приложения силы не совпадает
с центром тяжести сечения (точка С).
Условие прочности записывается в виде
,
−
нормальная сила;
−
изгибающие моменты соответственно
осей
;
−
площадь поперечного сечения;
− осевые моменты инерции сечения;
− координаты опасной точки (точки
наиболее удаленной от нейтральной
оси).
Для данной задачи имеем
где
− координаты точки приложения силы Р
(координаты
полюса силы).
2. Определение геометрических характеристик сечения бруса
Радиусы инерции сечения
3. Определение положения нейтральной линии и опасных точек сечения
При внецентренном
растяжении-сжатии нейтральная линия
не проходит через центр тяжести
поперечного сечения, ее положение
определяется отрезками
,
которые она отсекает на координатных
осях (рис. 10.6):
|
|
|
Рис. 10.6 |
Полученные точки позволяют провести нейтральную линию (рис. 10.6). Опасными точками сечения будут точки А и В.
4. Определение нормальных напряжений в опасных точках сечения и сравнение их с допускаемыми напряжениями
В точке В
в точке Е
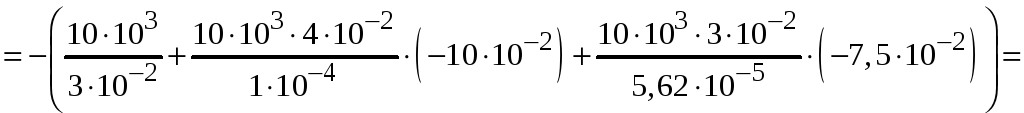
Условия прочности выполняются.
5. Построение эпюры нормальных напряжений
Для построения эпюры напряжений определим их в точках К и D.
в точке К
в точке D
Полученные значения напряжений позволяют построить эпюру нормальных напряжений в сечении бруса (рис. 10.7).
Рис. 10.7