Сопромат / Руководство к практическим занятиям по сопротивлению материалов / Раздел_5

49

Тема практического занятия № 5: Прямой сдвиг И ПРАКТИЧЕСКИЕ РАСЧЁТЫ НА ПРОЧНОСТЬ СОЕДИНЕНИЙ, РАБОТАЮЩИХ НА СДВИГ И СМЯТИЕ

5.1. Краткие сведения из теории

Прямым сдвигом называют такой вид нагружения стержня, при котором в его поперечных сечениях с площадью возникает только перерезывающая сила как равнодействующая действующих в сечении касательных напряжений , т.е.

.

На рис. 5.1а приведен пример соединения двух листов с помощью болта , поставленного без зазора, растягивающихся силами . Болт срезается возникающими в поперечном сечении касательными напряжениями , которые распределены по сечению неравномерно (рис. 5.1б). Кроме того, в продольном диаметральном сечении болта от давления листов возникают нормальные напряжения , называемые нормальными напряжениями смятия материала (рис. 5.1в). Это давление может быть настолько большим, что материал листа или болта начнет пластически деформироваться и отверстие в листах приобретет овальную форму.

а)	б) в)
Рис. 5.1

Таким образом, в болте возникают как касательные , так и нормальные напряжения , т.е. сложное напряженное состояние. Теоретическое исследование такого напряженного состояния практически невозможно. В то же время расчет болтов, заклепок, шпонок, сварных швов и др., которые не являются стержнями, встречается буквально на каждом шагу при проектировании и конструировании. В основу расчета на прочность таких соединений берут крайне упрощенные схемы, при помощи которых находятся условные средние напряжения

.

Расчет на прочность состоит в том, что напряжения не должны превышать некоторые условные допускаемые напряжения и , т.е.

.

Такие расчеты на прочность называются условными.

Обычно принимается , где − допускаемое напряжение при обычных расчетах стержней на растяжение-сжатие, а .

Поскольку расчетные напряжения являются условными, то их допускаемые значения могут быть определены только из опытов в аналогичных условиях нагружения, которые реализуются в конкретном крепежном соединении.

Практические расчёты заклепочных соединений базируются на предположениях:

1. В поперечном сечении болта или заклёпки возникает только один внутренний силовой фактор − поперечная сила Q.

2. Касательные напряжения, возникающие в сечении крепежного элемента, распределены по его площади равномерно.

3. Если соединение выполнено несколькими одинаковыми элементами то принимается, что все они загружены одинаково.

4. При расчёте на смятие учитывается не фактическая площадь смятия, а её проекция на диаметральную плоскость ().

При расчёте сварных соединений вводятся допущения:

1. По длине сварного шва независимо от его расположения по отношению к линии действия внешней силы напряжение распределяется равномерно.

2. Разрушение сварного шва происходит от среза по плоскости, проходящей через биссектрису прямого угла треугольного шва, то есть расчётная толщина шва принимается равной h = 0,7K (рис. 5.2).

Рис. 5.2

5.2. Примеры решения задач

№1. Проверить прочность заклёпочного соединения (рис. 5.3). Принять: допускаемое напряжение на растяжение полосы = 160 МПа; допускаемое напряжение на срез ; допускаемое напряжение на смятие = 320 МПа.

Рис. 5.3

Решение

1. Построим эпюру нормальных сил действующих в сечениях 1-1, 2-2, 3-3 полосы (рис. 5.3)

При этом будем учитывать, что на каждую заклёпку приходиться сила, равная в среднем

т.к. число заклёпок i = 5.

2. Проверка прочности полосы при растяжении

Расчёт необходимо выполнить для сечения 3-3, т.к. здесь действует наибольшая нормальная сила

.

Для сечения 2-2 усилие меньше

и расчётная площадь поперечного сечения меньше, чем в сечении 3-3.

Сечение 3-3

где 12∙(180-22) = 1896 мм² =1,896∙10^-3 м² – площадь поперечного сечения полосы в сечении 3-3 (рис. 5.4а).

.

Условие прочности выполняется.

Сечение 2-2

где 12∙(180-2·22) = 1632 мм² = 1,632∙10^-3 м² – площадь поперечного сечения полосы в сечении 2-2 (рис. 5.4б).

.

Условие прочности выполняется.

а)		б)
Рис. 5.4

3. Проверка прочности заклёпок на срез

Условие прочности

где − перерезывающая сила, приходящаяся на одну заклёпку; − площадь среза заклёпки.

Условие прочности выполняется.

4. Проверка прочности заклёпок на смятие

Условие прочности

где 22·12 = 264 мм² = 2,64∙10 ^-4 м² − условная площадь смятия.

Условие прочности выполняется.

5. Проверка условия прочности на срез по длине а (см. рис. 5.3)

Условие прочности

где 2·45·12 = 1080 мм² = 1,08·10 ^-3 м² − площадь среза.

Условие прочности выполняется.

Таким образом, прочность данного заклёпочного соединения обеспечена.

№2. Определить размеры детали А из условия равнопрочности на растяжение, срез и смятие (рис. 5.5), если

Рис. 5.5

Решение

Нарушение прочности данного соединения возможно от растяжения по сечению 1; от смятия по сечению 2 и от среза по сечению 3.

1. Определение допускаемой нагрузки Р из условия прочности стрежня диаметром на растяжение

Условие прочности

откуда

(1)

где − площадь поперечного сечения стержня диаметра . Из (1) следует, что

2. Определение размера D из условия прочности на смятие

Условие прочности

где − площадь смятия.

Тогда

откуда

примем D = 42 мм.

3. Определение размера h из условия прочности на срез

Условие прочности

где − площадь среза.

Условие прочности примет вид

откуда

Примем мм.

№3. Определить необходимую длину фланговых швов для прикрепления стержня фермы, состоящего из двух равнобоких уголков (рис. 5.6). Принять N = 320 кН; = 160 МПа; = 110 МПа.

Решение

1. Расчёт стержня фермы на прочность

Стержень фермы, состоящий из двух равнобоких уголков, растягивается силой Р, приложенной в центре тяжести сечения (рис. 5.6, точка ). Усилие, приходящееся на один уголок

.

Рис. 5.6

Усилие приложено в центре тяжести уголка (рис. 5.6, точка ). Условие прочности уголка

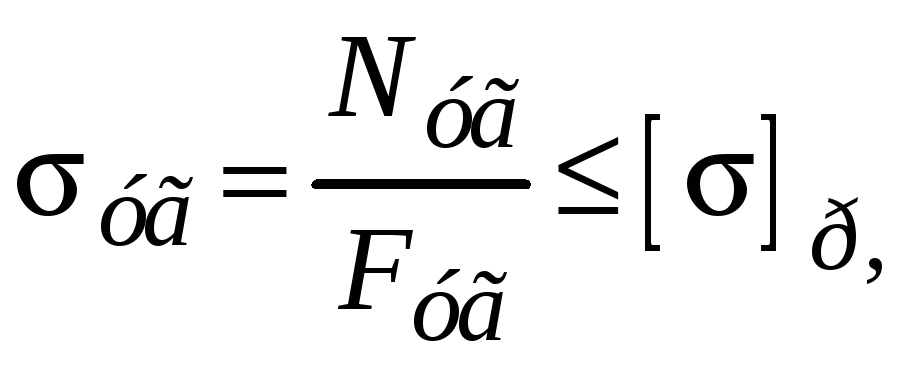
откуда необходимая площадь поперечного сечения уголка

По сортаменту выбираем уголок с ближайшей большей площадью поперечного сечения. Принимаем уголок 7,57,50,8 (рис. 5.7). Из сортамента имеем = 11,5 см², b = 7,5 см, 2,15 см, t = 0,8 см.

Рис. 5.7	Рис. 5.8

2. Определение длины сварных швов и

Рассмотрим равновесие уголка под действием сил , и (рис. 5.8).

Составим уравнения равновесия и определим усилия и , возникающие в сварных швах.

,

.

,

Условие прочности для сварного шва

,

откуда

Определим длину :

Примем = 190 мм. Определим длину :

Примем = 80 мм.