41

Тема практического занятия № 4:

Внутренние моменты и напряжения при кручении

4.1. Краткие сведения из теории

При кручении стержня (рис. 4.1а) в его поперечном сечении возникает крутящий момент (рис. 4.1).

Рис. 4.1

Методом сечений определяем внутренний момент (рис. 4.1б):

. (4.1)

Крутящий момент считаем положительным, если он вращает против часовой стрелки, если смотреть на него со стороны внешней нормали к сечению. Соответственно (4.1) позволяет построить график-эпюру изменения в виде прямой линии при

Дифференцируя (4.1), получаем зависимость Журавского

,

связывающую внутренний и внешний распределенный момент .

Из этой зависимости следуют простые правила контроля правильности построения эпюры внутренних крутящих моментов:

1. на незагруженном участке стержня (m = 0), ;

2. на равномерно загруженном участке стержня (m = const) момент

−

прямая линия, возрастающая при m < 0 и убывающая при m > 0;

3. в сечении, где действует сосредоточенный момент, в эпюре наблюдается скачок на величину этого момента.

Угол поворота поперечного сечения стержня определяется по формуле

,

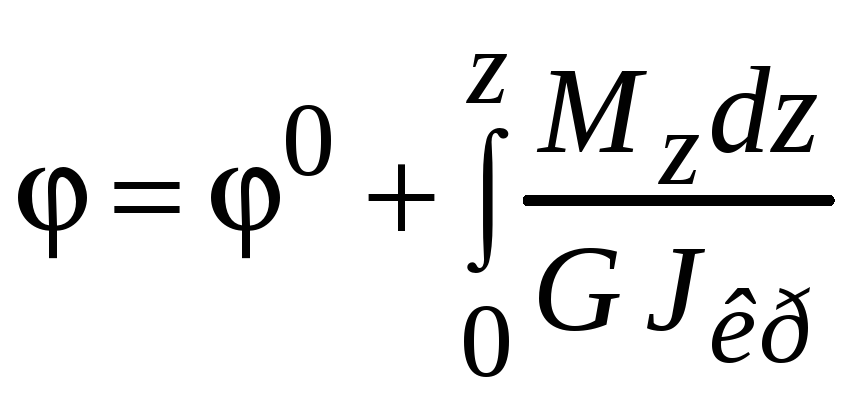где – угол поворота левого торцевого сечения в начале координат, – жесткость при кручении; G – модуль сдвига Кулона; – геометрическая жесткость при кручении стержня.

Если , то

.

При получаем угол поворота правого торцевого сечения относительно левого:

; , ().

На рис. 4.2 изображена эпюра касательных напряжений для различных поперечных сечений. Максимальное напряжение в поперечном сечении и условие прочности имеют вид

,

где – допускаемое касательное напряжение; – геометрический момент сопротивления сечения кручению.

Рис. 4.2

Для круглого поперечного сечения диаметра (рис. 4.2а)

.

Для кольцевого сечения (рис. 4.2б)

.

Для тонкостенной трубки толщиной и радиусом

.

Для прямоугольного сечения со сторонами (рис. 4.2в)

, .

Момент сопротивления и геометрическая жесткость содержат множители и , зависящие от отношения сторон . Значения коэффициентов приведены в таблице:

	1	1,5	1,75	2	3	5	10	∞
α	0,208	0,231	0,239	0,246	0,276	0,299	0,313	1/3
β	0,141	0,196	0,214	0,229	0,263	0,299	0,313	1/3
γ	1	0,859	0,820	0,795	0,753	0,743	0,742	0,742

Сечения тонкостенных стержней открытого профиля (узкий прямоугольник, двутавр, швеллер, уголок и др.) состоят из прямоугольников, для которых обычно , поэтому для них имеют место расчетные формулы

, ,

где – номер прямоугольной части сечения тонкостенного профиля.

4.2. Примеры решения задач

№1. Для стержня (рис. 4.3а) построить эпюру крутящих моментов, угловых перемещений, написать условие прочности. Определить допускаемое значение диаметра стержня.

Решение

1. Определение опорного реактивного момента из уравнения равновесия

Из рис. 4.3а получаем

,

.

2. Определение внутренних крутящих моментов методом сечений

У стержня два участка с различными выражениями для внутреннего крутящего момента. Методом сечения находим (рис. 4.3б)

, ,

и строим эпюру крутящих моментов (рис. 4.3в).

В сечении на стыке участков действует сосредоточенный момент . В этом сечении на эпюре имеет место скачок на величину этого момента в сторону уменьшения . На незагруженных участках стержня, согласно дифференциальной зависимости Д. Журавского, , откуда , что соответствует построенной эпюре (рис. 4.3в).

а) в) г)	б)
Рис. 4.3

3. Расчет на прочность

Из эпюры крутящих моментов определяем во всех сечениях первого участка. Условие прочности

. (1)

Если сечение круглое, то

, (2)

и тогда из условия прочности (1) получаем

.

Если, например, , то

.

Округляем полученные значения до целых значений и принимаем . Делаем контрольную проверку условия прочности при новом значении диаметра D=7 см. В результате вычислений по формулам (1), (2) получаем

,

.

Перенапряжение составит , т.е. . Если принять D=8 см, то , , что меньше допускаемого напряжения на 25,4 %. Окончательно принимаем D=8 см.

4. Построение эпюры углов закручивания (рис. 4.3г)

На первом участке , поэтому

.

При а при .

На втором участке имеем

.

При получаем , а при .

№2. Построить эпюры крутящих моментов и угловых перемещений , произвести расчеты на прочность и жесткость (рис. 4.4).

Решение

1. Уравнения равновесия

Вычисляем сумму всех внешних моментов, действующих на стержень, круглого поперечного сечения и приравниваем ее к нулю

.

С учетом получим реактивный момент в заделке

.

2. Определение выражений крутящих моментов методом сечений и построение эпюры

Стержень имеет два участка, на которых выражения крутящих моментов различны. Рассекаем стержень на первом и втором участках и рассматриваем в каждом из этих случаев одну из отсеченных частей (рис. 4.4б).

а) в) г)	б) метод сечений
Рис. 4.4

Для первого участка ()

,

для второго ()

.

Строим эпюру крутящих моментов. На первом участке откладываем отрицательное постоянное значение . На втором участке эпюра – прямая линия. Для ее построения достаточно иметь две точки: при и . Соответствующие моменты и . Наносим на график эти точки и проводим прямую линию (рис. 4.4в). В сечениях, где действуют сосредоточенные моменты, имеют место скачки, равные по величине значениям этих моментов. Наибольший момент возникает в сечении :

.

3. Контроль правильности построенной эпюры с помощью дифференциальной зависимости Д. Журавского

,

позволяющей установить следующие правила:

на незагруженном участке эпюра постоянна;

на равномерно загруженном участке эпюра − прямая линия , возрастающая с ростом , если , и убывающая, если ;

в сечениях, где действует сосредоточенный момент, имеет место скачок на величину этого момента.

В нашем примере все правила контроля выполняются.

4. Расчет на прочность при кручении бруса

Условие прочности при кручении

.

Так как , то получаем

.

Если известны, то находим допустимое значение момента

.

При проектировочном расчете находим размер поперечного сечения, т.е. диаметр

.

В этом случае должны быть известны .

Третий тип расчета – проверочный.

5. Построение эпюры угловых перемещений (рис. 4.4г)

Угловые перемещения находим по формуле

,

где − номер участка, − значение угла в начале -го участка, − крутящий момент на -м участке, − координата начала -го участка, − жесткость при кручении на i-м участке.

На первом участке (защемление).

Угол поворота

.

Эпюра – прямая линия. При , при получим .

На втором участке

,

или

.

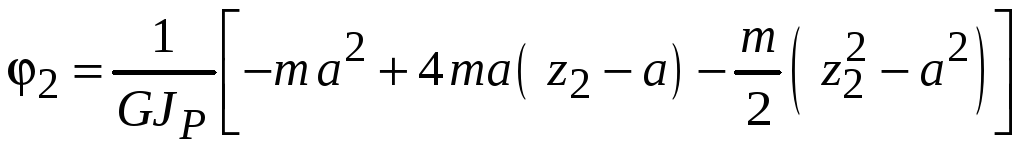График-эпюра − квадратичная парабола.

При получаем , при − .

Выпуклость параболы определяется знаком второй производной. Производные

Так как в задаче , то и выпуклость эпюры обращена кверху. Первая производная обращается в нуль при , что за пределами стержня, поэтому эпюра не имеет экстремума.

Помимо условия прочности иногда проверяется условие жесткости при кручении

,

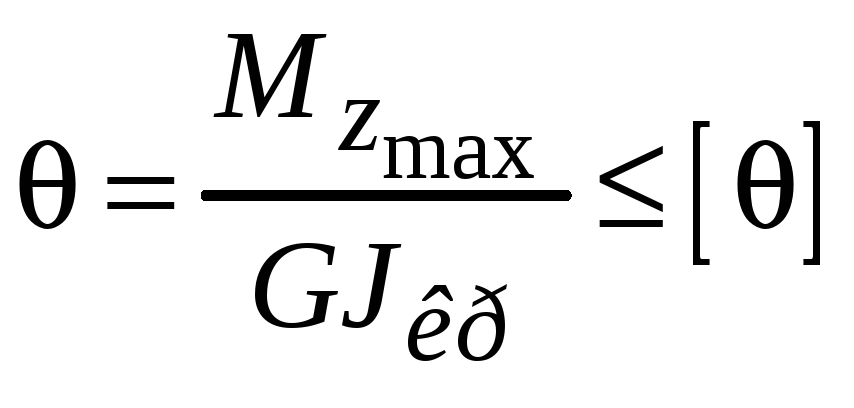где − относительный угол закручивания, − допускаемое значение относительного угла закручивания.

№3. Стальной консольный вал (рис. 4.5а), имеющий участки с разными поперечными сечениями (круглое и прямоугольное), нагружен внешними крутящими моментами. Требуется: из условия прочности определить допускаемую величину крутящих моментов; построить эпюры касательных напряжений для круглого и прямоугольного поперечных сечений; построить эпюру углов закручивания по длине вала.

Принять