4. Проверка поперечного сечения рамы на прочность

Условие прочности для рамы записывается в виде

Максимальный изгибающий момент действует в узле С на первом участке и составляет . Нормальная сила в этом сечении равна

Площадь поперечного сечения рамы (двутавр № 36) и момент сопротивления

Для дальнейших расчетов примем

Тогда

Напряжения

Из эпюры (см. рис. 8.17) видно, что сжимающие напряжения будут испытывать верхние волокна, а растягивающие – нижние, т.к. изгибающий момент сжимает верхние волокна и растягивает нижние.

Эпюры нормальных напряжений приведены на рис. 8.20.

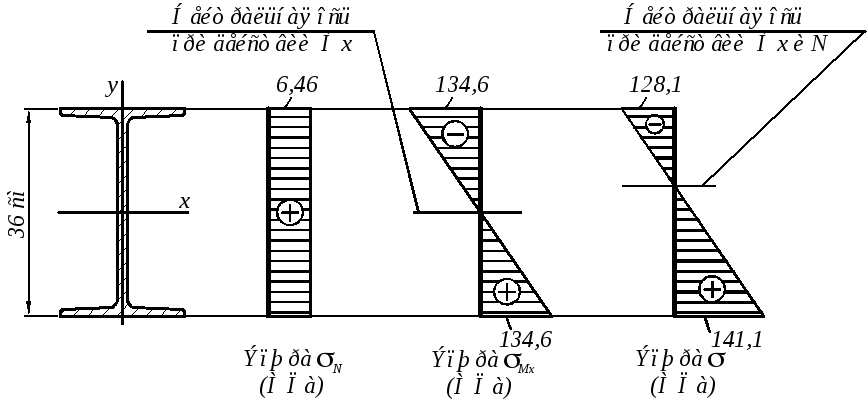
Рис. 8.20

Сравнив максимальное напряжение с допускаемым, видно, что условие прочности выполняется:

№13. Для рамы с внутренним шарниром (рис. 8.21) построить эпюры и определить допускаемое значение внешней нагрузки , если и поперечное сечение двутавр № 33.

Решение

1. Определение опорных реакций из уравнений равновесия

Заданная рама имеет четыре простые связи и один внутренний шарнир, который снимает одну простую связь. Следовательно, рама статически определимая (рис. 8.21а). Составим уравнения равновесия:

Из уравнений равновесия получим

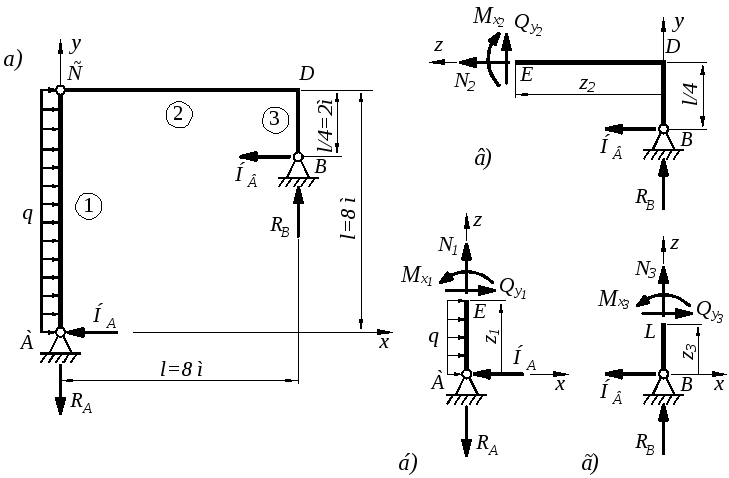
Рис. 8.21

Для проверки правильности определения опорных реакций спроецируем все силы на ось :

Полученное уравнение тождественно уравнивается, следовательно, реакции определены верно.

2. Разбиваем раму на силовые участки 1, 2, 3

3. Используя метод сечений составим выражения для и построим их эпюры

Первый участок , (рис. 8.21б).

Рассматривая равновесие нижней отсеченной части, составим уравнения статики (равновесия)

Внутренние силовые факторы на первом участке

Полагая (точка А), получим

при (точка С)

Определим экстремальное значение изгибающего момента

Второй участок , (рис. 8.21в)

Рассматривая равновесие правой отсеченной части, получим уравнения статики

Внутренние силовые факторы на втором участке

Полагая (точка D), получим при (точка С)

Третий участок , (рис. 8.21г)

Уравнения равновесия

Внутренние силовые факторы на третьем участке

Полагая (точка B), получим при (точка D)

Согласно полученным выражениям для строим эпюры (рис. 8.22).

Рис. 8.22

Для статической проверки вырезаем узлы рамы и прикладываем к ним внутренние силы и моменты, составляем уравнения равновесия (рис. 8.23, 8.24).

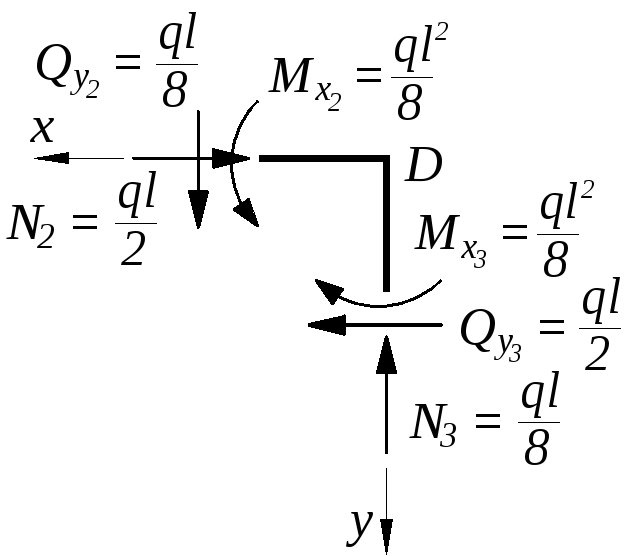
	Узел С
Рис. 8.23

	Узел D
Рис. 8.24

Поскольку уравнения равновесия выполняются тождественно, следовательно, узлы рамы находятся в равновесии.

4. Определение допускаемого значения внешней нагрузки

Условие прочности для стержней рамы имеет вид

Из анализа эпюр и (см. рис. 8.22) видно, что опасное сечение будет в точке D на 2-м участке, т.к. здесь действует и нормальная сила, имеющая наибольшее по модулю значение

Из таблиц сортамента выпишем необходимые геометрические характеристики для двутавра № 33:

Теперь условие прочности принимает вид

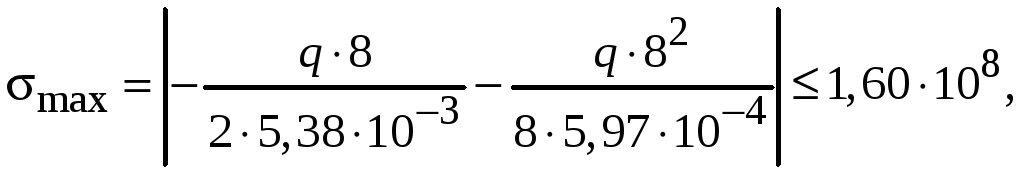
откуда

№14. Построить эпюры для балки (рис. 8.25) и подобрать стандартное двутавровое поперечное сечение, если