140

Тема практического занятия № 12: изгиб бруса большой кривизны

12.1. Краткие сведения из теории

Брусья с криволинейной осью различаются:

на брусья большой кривизны, если отношение

брусья малой кривизны, если отношение

где R – радиус кривизны бруса; h – высота поперечного сечения (рис. 12.1).

Рис. 12.1

Расчётные формулы для напряжений в случае прямого бруса справедливы и к брусу малой кривизны.

При рассмотрении бруса большой кривизны предполагается, что:

1. кривой брус является плоским (т.е. его ось является плоской кривой);

2. поперечное сечение бруса симметрично относительно плоскости, в которой расположена его ось, а внешние силы действуют в этой плоскости;

3. поперечные сечения бруса, плоские до деформации, остаются плоскими и после деформации (гипотеза плоских сечений);

4. продольные изогнутые волокна находятся в одноосном напряжённом состоянии (давление продольных волокон бруса друг на друга не учитывается).

Рис. 12.2

Внутренние усилия в поперечном сечении кривого бруса определяются методом сечений и приводятся к нормальной силе N, поперечной силе и изгибающему моменту (рис. 12.2). Нормальная сила N считается положительной, если она вызывает растяжение, поперечная сила положительная, если она вращает отсечённую часть бруса относительно начала участка по часовой стрелке; изгибающий момент больше нуля, если он увеличивает кривизну бруса (рис. 12.2). На эпюрах N, и положительные значения будем откладывать перпендикулярно геометрической оси бруса от центра его кривизны, а отрицательные значения – к центру его кривизны.

Для кривого бруса дифференциальные зависимости между внутренними силовыми факторами и внешней нагрузкой имеют иную форму, чем для прямолинейного. Рассмотрим элемент кривого бруса с криволинейной осью радиуса R (рис. 12.3).

Рис. 12.3

Равнодействующая внешней нагрузки q, приложенная к элементу , даёт проекцию на нормаль и на касательную . При переходе от сечения А к сечению В внутренние силовые факторы N, и изменяются и получают приращение dN, и . В силу малости угла

(12.1)

Составим уравнения равновесия для элемента АВ:

Учитывая соотношения (12.1) и пренебрегая членами второго порядка получим

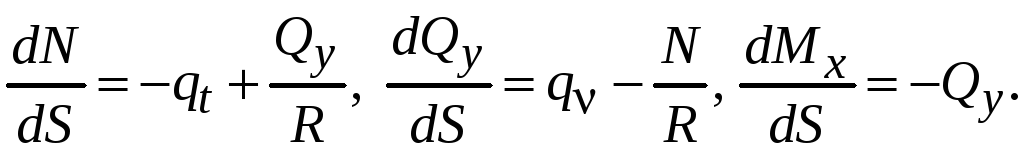
При чистом изгибе (, ) нормальные напряжения в поперечном сечении кривого бруса находят по формуле

где – изгибающий момент в сечении кривого бруса; R – радиус кривизны оси бруса; F – площадь поперечного сечения; y – расстояние от центральной оси сечения (ось x) до точки, где определяется напряжение; – радиус кривизны нейтральной линии (рис. 12.4).

Рис. 12.4

При изгибе кривого бруса нейтральная линия смещена по отношению к геометрической оси бруса к центру кривизны на величину . В частности для прямоугольного сечения

где , – радиусы кривизны соответственно наружного и внутреннего волокна сечения; h – высота сечения;

Для других форм поперечного сечения величина приведена в соответствующих справочниках и учебной литературе.

Если кривой брус подвергается продольно-поперечному изгибу, то в его поперечных сечениях кроме изгибающего момента возникают нормальная и перерезывающая силы N и . В этом случае нормальные напряжения определяются по формуле

Перерезывающая сила возникает за счёт касательных напряжений , которые приближённо можно вычислить по формуле Журавского.

11.2. Примеры решения задач

№1. Для бруса с криволинейной осью (рис. 12.5) построить эпюры внутренних силовых факторов (N, , ) и найти нормальные напряжения в опасном сечении бруса.