
schoolbook_1
.pdf
81
Решение. Разделив обе части уравнения на y2 , получим: xy 2 y 1 ln x.
|
|
|
|
|
|
|
1 |
|
y |
|
|
1 |
|
z |
|
|
|
||
Введем новую переменную |
z |
y |
, тогда |
|
y2 |
y |
. Подставляя в уравнение, |
||
получим: xz z ln x. Это линейное уравнение относительно функции z . Применим метод вариации произвольной постоянной:
xz z 0, |
|
x |
dz |
z, |
dz |
|
dx |
, ln z ln x lnC, |
Z Cx, |
z C x x, |
||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
z |
|
|
x |
|
|
|
|
|
|
|
|
|
||||||||||||
z |
|
|
|
C x , |
|
|
|
|
|
x C x C x x ln x, x |
2 |
|||||||||||||||||||||||||||
|
|
|
C x x |
x C x |
|
C |
x ln x, |
|||||||||||||||||||||||||||||||
x2 |
dC |
|
lnx, dC |
ln x |
dx, C |
|
lnx |
dx C . |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
x2 |
1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
Интегрируя по частям, находим |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
ln x |
1 |
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
ln x |
|
dx |
|
|
ln x |
|
|
C1, следовательно, |
|||||||||||||||||||||||
|
x2dx |
x |
x2 |
x |
x |
|||||||||||||||||||||||||||||||||
C |
1 |
ln x 1 C , а z ln x 1 C x. Заменяя теперь z на |
1 |
, получим: |
||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
y |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
ln x 1 C x или y |
|
|
|
|
. Это и есть общее решение исходного |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
y |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
C1x ln x 1 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
уравнения.
Глава 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
§1. Уравнения вида y n f x
Решение данного уравнения получается последовательным интегрированием его левой и правой частей.
Пример. Найти частное решение уравнения y sin 2x, удовлетворяющее
начальным условиям: y 0 0, |
|
|
|
|
y |
|
|
||||||||||
y |
0 1, |
0 0. |
|||||||||||||||
|
|
Решение: y |
|
|
|
y |
|
|
1 |
|
cos2x C1, |
||||||
|
|
|
|
|
|||||||||||||
|
|
dx sin2xdx, |
|
||||||||||||||
|
|
|
1 |
|
|
|
1 |
|
|
2 |
|
|
x2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y |
|
4sin2x C1x C2, |
y |
8cos2x C1 |
2 |
C2x C3. |
|||||||||||
|
|||||||||||||||||
Это и есть общее решение. Чтобы найти частное решение, удовлетворяющее заданным начальным условиям, достаточно определить соответствующие значения C1,C2,C3:
0 |
1 |
C , |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
1 |
1 |
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|||||
1 C2, |
C1 |
|
|
, |
C2 1, |
C3 |
|
|
. |
|||
|
|
|||||||||||
|
1 |
|
C3, |
2 |
|
|
|
8 |
|
|||
0 |
|
|
|
|
|
|
|
|
|
|
||
3 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
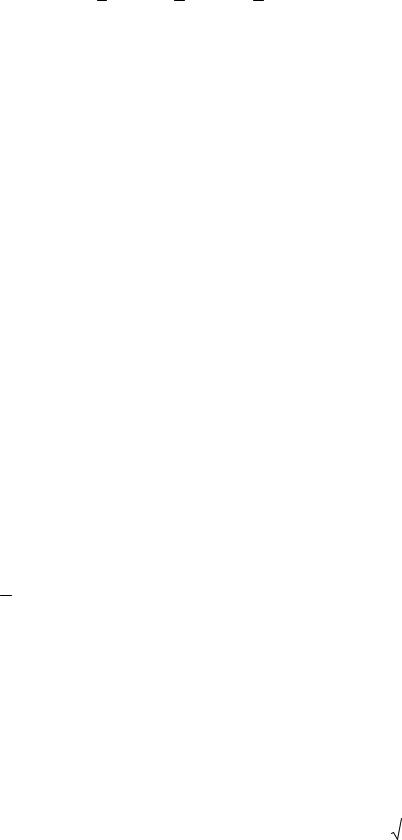
82
Таким образом, искомое частное решение имеет вид:
y 1cos2x 1 x2 x 1 . 8 4 8
§2. Некоторые типы дифференциальных уравнений второго прядка, приводимые к уравнениям первого порядка
2.1. Уравнения не содержащие y
Уравнение вида y f x, y не содержит явным образом искомой функции y. Порядок такого уравнения может быть понижен с помощью подстановки y p.
|
Пример. Решить уравнения x3y x2 y 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
Решение. Положим y p, |
тогда y |
|
dp |
, и мы получаем |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
дифференциальное уравнение первого порядка относительно |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
вспомогательной функции p: |
x |
3 dp |
x |
2 |
p 1. Это уравнение является |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
dx |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
линейным. Найдем его общее решение, используя метод вариации |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
dp |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
произвольной постоянной. |
x |
|
|
|
|
x |
|
|
p 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
dp |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
C |
|
|
|
|
|
|
C x |
|
|
dp |
|
|
1 |
|
dC |
|
|
1 |
|
||||||||||
|
|
, |
ln p ln x lnC, |
|
p* |
, |
|
|
|
p* |
, |
|
|
|
|
C x , |
|||||||||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
x2 |
||||||||||||||||||||||||||||||||||||||
|
p |
|
1 |
|
|
|
|
1 |
|
|
|
|
|
C x |
|
|
|
|
|
|
x |
|
dC |
|
|
x |
|
dx |
|
x dx |
|
|
|||||||||||||||||||
|
|
|
|
dC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
1 |
|
|
||||||||||||||||
|
x3 |
|
|
|
|
|
|
|
|
|
|
C x x2 |
|
|
|
|
1, x2 |
|
|
|
|
|
|
|
1, dC |
|
|
|
, |
C x |
|
|
C |
||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
dx |
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
1 |
||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
C1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Итак, p x2 |
x |
, т.е. |
y |
|
x2 |
|
|
|
x |
|
|
. Следовательно, |
|
|
|
|
||||||||||||||||||||||||||||||||||
1
y x C1 ln x C2 .
Замечание. Аналогичным способом можно проинтегрировать уравнение y n f x, y n 1 , полагая y n 1 p.
2.2. Уравнения, не содержащие x
Уравнение вида y f y, y не содержит явным образом независимую переменную x. Порядок этого уравнения также может быть понижен. И в этом случае полагаем y p, но теперь мы будем считать p функцией от y
(а не от x, как прежде). |
|
|
1 |
|
|
|
|
Пример. Найти частное решение уравнения y |
|
|
, удовлетворяющее |
||||
|
y |
||||||
|
|||||||
|
|
3 |
|
|
|
||
начальным условиям y 1 0, |
|
1 0. |
|
|
|
||
y |
|
|
|
||||
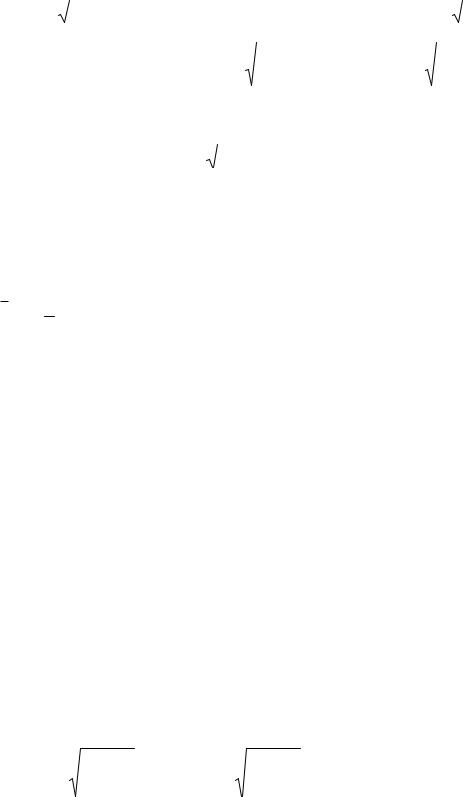
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
83 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Данное уравнение не содержит x. Положим y p, |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
рассматривая p как функцию от y. Тогда y |
|
p |
dp |
, и мы получаем |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
уравнение первого порядка относительно вспомогательной функции p: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
p |
dp |
|
|
1 |
|
|
|
|
|
. Разделяя переменные, будем иметь: |
|
pdp |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
y |
|
|
|
|
ydy. Откуда |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
3 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
p2 |
|
|
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
y |
2 |
|
|
C1 |
или p |
|
|
y |
2 |
|
C1 , т.е. |
y |
|
|
|
y |
2 |
|
C1 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Здесь мы |
|||||||||||||||||||||||||||||||||||||||||||
2 |
3 |
|
3 |
|
|
|
|
9 |
3 |
|
|
|
|
|
3 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
можем сразу определить значение произвольной постоянной C1, используя |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
dy |
|
2 |
y |
3 |
. |
|||||||||||||||||||||||||||||||||||||||||
начальные условия: 0 |
|
|
|
|
|
|
|
|
|
, |
|
C 0. Следовательно, |
|
4 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
0 C |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
3 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Разделяя переменные и интегрируя, получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
y |
|
3 |
|
|
|
|
|
|
|
|
|
2 |
dx, |
|
1 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
1 |
|
|
1 |
C2 x . Пользуясь тем, что |
|||||||||||||||||||||||||||||||
4dy |
4y4 |
x |
C2 |
или y4 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
3 |
3 |
6 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
y 1 0, найдем C2: C2 1. Искомое частное решение запишется:
1
y4 1 x 1 . 6
2.3. Линейные однородные уравнения с постоянными коэффициентами
Рассмотрим линейное однородное уравнение второго порядка с постоянными коэффициентами, т.е. уравнение y py qy 0, где p и q - постоянные числа.
Чтобы найти общее решение этого уравнения, достаточно найти два линейно независимых частных решения в виде y ekx, где k Const.
Подставляя эту функцию и ее производные y kekx и y k2ekx в
рассматриваемое уравнение, получим: ekx k2 pk q 0. Так как ekx 0,
значит k2 pk q 0.
Следовательно, если k будет удовлетворять полученному уравнению, которое называется характеристическим, то ekx будет решением исходного уравнения.
Характеристическое уравнение есть квадратное уравнение, имеющее два корня: обозначим их через k1 и k2 . При этом
|
|
p |
|
p2 |
|
|
|
p |
p2 |
||
k |
|
|
|
|
q, k |
2 |
|
|
|
|
q. |
|
|
|
|
||||||||
1 |
2 |
4 |
|
|
2 |
|
4 |
|
|||
|
|
|
|
|
|
||||||
Здесь возможны следующие случаи:

84
а) Корни характеристического уравнения действительны и различны.
В этом случае частными решениями будут функции y1 ek1x и y2 ek2x. Общим решением уравнения будет Y C1ek1x C2 xek2x .
Пример. Решить уравнение y y 6y 0.
Решение. Характеристическое уравнение имеет вид k2 k 6 0. Корни характеристического уравнения: k1 2, k2 3. Общее решение:
YC1e2x C2e 3x.
б) Корни характеристического уравнения действительные и равные.
Вэтом случае мы имеем только одно частное решение y ekx, т.к. k1 k2 k. При этом общее решение будет Y C1ekx C2xekx.
Пример. Решить уравнение y 6y 9y 0.
Решение. Составим характеристическое уравнение k2 6k 9 0. Найдем его корни: k1 3, k2 3. Общим решением будет функция
YC1e 3x C2xe 3x .
в) Корни характеристического уравнения комплексные.
Так как коэффициенты p и q характеристического уравнения действительные числа, то комплексные корни будут сопряженными. Причем,
k |
i , k |
|
i , где |
p |
q |
p2 |
|
|
|
|
2 |
|
, |
|
. Общее решение в |
||||||
|
|
|||||||||
1 |
|
|
2 |
|
|
4 |
|
|
|
|
рассматриваемом случае имеет вид Y e x C |
cos x C |
2 |
sin x . |
|||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
Пример. Найти частное решение уравнения y 2y 5y 0, |
|||||||||
удовлетворяющее начальным условиям y 0 0, |
|
|
|
|||||||
y 0 1. |
||||||||||
Решение. Составим характеристическое уравнение k2 2k 5 0. Найдем его корни k1,2 1 2i. Следовательно, общее решение есть
Y e x C1 cos2x C2 sin2x . Найдем теперь частное решение, удовлетворяющее заданным начальным условиям. На основании первого условия находим 0 e 0 C1 cos0 C2 sin0 , откуда C1 0. Заметив, что y e x 2C2 cos2x e xC2 sin2x, из второго условия получаем: 1 2C2, т.е.
|
1 |
1 |
|
x |
|
||
C2 |
|
|
. Таким образом, искомое частное решение есть y |
|
e |
|
sin2x. |
|
|
|
|||||
|
2 |
2 |
|
|
|
||
2.4. Линейные неоднородные уравнения с постоянными коэффициентами
85
Линейные неоднородные уравнения второго порядка с постоянными коэффициентами имеют вид y py qy f x , где p и q - действительные числа.
Общее решение линейного неоднородного уравнения представляется как сумма какого-нибудь частного решения y* этого уравнения и общего решения Y соответствующего однородного уравнения, т.е. y Y y*.
Вид частного y*решения неоднородного уравнения зависит от вида правой части этого уравнения. Рассмотрим некоторые случаи.
а) f x a |
2 |
x2 a x a |
0 |
a |
2 |
0 . Если q 0, то частное решение |
|
1 |
|
|
неоднородного уравнения ищем также в форме квадратного трехчлена:
y* A2x2 A1x A0 , где A2, A1, A0 - неопределенные коэффициенты. Если
q 0, то частное решение y* ищем в виде y* x(A2x2 A1x A0), когда один из корней характеристического уравнения равен нулю, и в виде
y* x2(A x2 |
A x A ), когда оба корня характеристического уравнения |
||||||||
2 |
1 |
0 |
|
|
|
f x - многочлен P x произвольной |
|||
нули. Аналогично обстоит дело, если |
|||||||||
степени. |
|
|
|
|
|
|
|
|
|
Пример. Решить уравнение y y 2x 1. |
|
|
|
||||||
Имеем: k2 k 0, |
k 0, |
k |
2 |
1, |
Y C |
C |
2 |
e x. Так как ноль – |
|
|
|
1 |
|
|
1 |
|
|
||
однократный корень характеристического уравнения, то частное решение
данного уравнения ищем в виде y* x(A x A ). Отсюда имеем: |
|
|||
|
|
1 |
0 |
|
y* 2A x A , |
y* 2A . Подставляем в исходное уравнение: |
|
||
1 |
0 |
1 |
|
|
2A1 2A1x A0 |
2x 1. Искомые коэффициенты будут: A1 1, A0 |
1. |
||
Значит, частное решение будет y* x2 x, а общее решение получается в
виде y C |
C |
2 |
e x x2 x. |
1 |
|
|
|
б) f x aebx |
a 0 . Частное решение ищем в виде y* Aebx, где A - |
||
неопределенный коэффициент. Если b- корень характеристического уравнения, то частное решение ищем в виде y* Axebx, когда b -
однократный корень, и в виде y* Ax2ebx, когда b - двукратный корень.
Аналогично будет, если f x P x aebx , где P x - многочлен.
Пример. Решить уравнение y 2y y 2ex . |
|
|
|
|||||
Имеем: k2 2k 1 0, k |
k |
2 |
1, |
Y C |
C |
2 |
x ex |
. Так как в |
1 |
|
|
1 |
|
|
|
||
характеристическом уравнении корень имеет кратность, равную двум, то частное решение данного уравнения ищем в виде y* Ax2ex . Далее имеем:
86
y* Ax x 2 ex , |
y* A x2 4x 2 ex , |
|
|||
Aex x2 4x 2 2Axex x 2 Ax2ex |
2ex, |
A 1, |
|||
y* x2ex , y C C |
2 |
x ex x2ex |
|
|
|
1 |
|
|
|
|
|
в) f x acos x bsin x (a и b не нули одновременно). В этом случае частное решение y* ищем также в форме тригонометрического двучлена y* Acos x Bsin x, где A и B - неопределенные коэффициенты.
В случае p 0, |
|
q 2 |
(или когда i |
|
- корни характеристического |
||||||||||
уравнения) частное решение исходного уравнения ищем в виде |
|
||||||||||||||
y* x Acos x Bsin x . |
|
|
|
|
|
|
|
|
|
|
|
||||
Пример. Решить уравнение y y cosx. |
|
|
|
|
|
|
|||||||||
Решение. Имеем: k2 1 0, k i, |
k |
2 |
i, |
Y C cosx C |
2 |
sin x. Так как |
|||||||||
|
|
|
1 |
|
|
|
|
|
|
1 |
|
||||
i - корни характеристического уравнения, то частное решение данного |
|||||||||||||||
уравнения ищем в виде y* x Acosx Bsin x . Далее имеем: |
|
|
|||||||||||||
y* Acosx Bsin x x Asin x Bcosx , |
|
|
|
|
|
|
|||||||||
y* 2Asin x 2Bcosx x Acosx Bsin x , |
|
|
x |
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
* |
|
|
|
|||
2Asin x 2Bcosx cosx, A 0, |
B |
|
|
, y |
|
|
|
sin x, |
|
|
|||||
2 |
|
2 |
|
|
|||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||
y C cosx C |
2 |
sin x |
sin x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для рассматриваемых дифференциальных уравнений справедлива так называемая теорема наложения, которая позволяет отыскивать частное решение в более сложных случаях.
Теорема. Если y1 является решением уравнения y py qy f1 x , а y2 решением уравнения y py qy f2 x , то y1 y2 есть решение уравнения y py qy f1 x f2 x .
Пример. Найти общее решение уравнения y 2y 1 2ex sinx.
Решение. Характеристическое уравнение k2 2k 0 имеет корни
k |
0, k |
2 |
2. Следовательно, Y C |
C |
2 |
e 2x |
. Находим частное решение |
|||||
1 |
|
|
|
|
1 |
|
|
|
|
|
||
y1* |
уравнения y 2y 1 в виде y1* |
Ax, тогда y1* A, |
y1* 0. Отсюда |
|||||||||
0 2A 1, |
A |
1 |
. Следовательно, |
y* |
|
1 |
x. |
|
|
|||
|
|
|
2 |
|
1 |
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
||||

|
87 |
|
|
|
|
|
Частное решение y2* уравнения y 2y 2ex |
ищем в форме y2* Bex. |
|||||
Тогда y2* Bex, |
y2* Bex . Отсюда Bex |
2Bex |
2ex , 3B 2, |
B |
2 |
. |
|
||||||
|
|
|
|
3 |
|
|
Следовательно, y2* 2ex . 3
Наконец, находим частное решение y3* уравнения y 2y sin x в форме
y3* Ccosx Dsin x, тогда |
y3* Csin x Dcosx, |
y3* Ccosx Dsin x. |
||||||||||
Подставляя в уравнение, получим: |
|
|
|
|
|
|
|
|||||
Ccosx Dsin x 2Csin x 2Dcosx sin x. Отсюда имеем: |
|
|
||||||||||
C 2D 0, |
|
|
2 |
|
1 |
|
* |
2 |
|
1 |
|
|
|
Значит C |
|
|
, D |
|
. Следовательно, y3 |
|
cosx |
|
sin x. |
||
5 |
5 |
5 |
5 |
|||||||||
D 2C 1. |
|
|
|
|
|
|
|
|||||
По теореме наложения частное решение исходного уравнения будет:
y* y* |
y* |
y* |
|
1 |
x |
2 |
ex |
|
2 |
cosx |
1 |
sin x, тогда общее решение |
||||||||||
|
|
|
|
|
||||||||||||||||||
1 |
2 |
3 |
2 |
|
3 |
|
5 |
|
5 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
запишется так: y C |
C |
2 |
e 2x |
|
1 |
x |
2 |
ex |
|
2 |
cosx |
1 |
sin x. |
|||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
1 |
|
|
|
2 |
3 |
|
|
5 |
5 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2.5. Метод вариации произвольных постоянных (метод Лагранжа)
Этот метод применяется для отыскания частного решения y* линейного неоднородного уравнения, когда известно общее решение соответствующего линейного однородного уравнения. Пусть дано линейное неоднородное уравнение второго порядка y py qy f x и пусть общим решением соответствующего однородного уравнения y py qy 0 является функция
YC1y1 C2 y2 .
Втакой же форме ищется и частное решение y* линейного неоднородного
уравнения, только C1 и C2 считаются не произвольными постоянными, а некоторыми, пока неизвестными функциями от x, т.е. полагаем, что
y* C1 x y1 C2 x y2. Дифференцируя это выражение дважды и подставляя его в исходное уравнение, получим уравнение относительно C1 x и C2 x .
Кроме того, в данном методе полагают, что C1 x y1 C2 x y2 0. Два последних уравнения образуют систему двух уравнений с двумя неизвестными C1 x и C2 x .
Интегрируя найденные значения, получим: C1 x 1 x dx и
C2 x 2 x dx. При этих значениях C1 x и C2 x получим частное решение y* C1 x y1 C2 x y2.
Пример. Найти общее решение уравнения y 4y 1 . sin 2x
88
|
Решение. Характеристическое уравнение k2 4 0 имеет корни k |
2i. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,2 |
|
|||
Значит, Y C1 cos2x C2 sin2x. Будем искать частное решение в форме |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
y* C x cos2x C |
2 |
x sin2x. C |
x и C |
|
x находим, решая систему |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
уравнений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
sin2x 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
C1 |
cos2x C2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
C |
|
2sin2x |
C |
2cos2x |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
sin2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
0 |
|
|
sin2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2x |
0 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
2cos2x |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2sin2x |
|
1 |
|
|
|
|
|
cos2x |
|
|
|||||||||||||
C |
|
|
|
|
|
|
sin2x |
|
|
|
|
, |
|
C |
|
|
|
|
|
|
|
sin2x |
|
|
|
|
. |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
cos2x |
|
|
|
sin2x |
|
2 |
|
|
|
|
|
|
cos2x |
|
sin2x |
|
|
|
||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2sin2x |
|
|||||||||||||||||||||||
|
|
|
|
|
2sin2x |
|
|
2cos2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2sin2x |
2cos2x |
|
|
|
|
|
|||||||||||||||||||||||
|
Интегрируя, находим: C |
|
1 |
x, |
C |
|
|
1 |
lnsin2x. Следовательно, |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y* |
xcos2x |
sin2xlnsin2x, а общее решение |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y C |
|
cos2x C |
2 |
sin 2x |
xcos2x |
sin2xlnsin 2x. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
§3. Системы дифференциальных уравнений
3.1. Общие определения. Сведение системы к одному дифференциальному уравнению высшего порядка
Системой дифференциальных уравнений называется совокупность уравнений, в каждое из которых входит независимая переменная, искомые функции и их производные.
Решение системы, состоящей из нескольких уравнений с таким же числом неизвестных функций, можно привести к решению дифференциального уравнения с одной неизвестной функцией.
Нормальная система уравнений:
|
dx1 |
|
f |
t, x , x |
|
|
,..., x |
|
|
, |
||||
|
|
|
|
|
||||||||||
dt |
1 |
1 |
2 |
|
|
n |
|
|
||||||
dx |
2 |
|
|
|
t, x1, x2,..., xn , |
|||||||||
|
|
|
f2 |
|||||||||||
dt |
|
|||||||||||||
.......... |
dxn |
|
.......... |
|
.......... |
|
|
|
.......... |
|
|
|
................................ |
|
|
|
f |
n |
t, x , x |
2 |
,..., x |
n |
, |
||||||
|
|
|||||||||||||
|
dt |
|
|
1 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
как правило, может быть заменена одним дифференциальным уравнением, порядок которого равен порядку системы.
Пример. Найти общее решение системы уравнений

|
|
|
|
|
|
|
89 |
|
|
|
|
|
dx |
|
y, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
dt |
|
|
|
|
|
|
|
|
|
|
|
dy |
|
z, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
dz |
|
x y z. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
dt |
|
|
|
|
|
|
|
|
|
|
|
Решение. |
Продифференцировав |
первое уравнение по |
t, |
заменим |
|||||||
|
|
|
|
|
dy |
|
d2x |
|
dy |
z. |
|
производную |
|
|
ее выражением |
из второго уравнения: |
|
|
|||||
|
|
dt2 |
dt |
||||||||
|
|
|
|
|
dt |
|
|
|
|||
Продифференцировав полученное уравнение еще раз, заменим производную
|
dz |
ее выражением из третьего уравнения: |
|
d3x |
|
|
dz |
x y z . Подставляя в |
||||||||||||||||||||||||
|
dt |
|
|
dt3 |
|
dt |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
последнее |
|
|
уравнение |
y |
dx |
|
и |
z |
|
|
d2x |
, |
|
|
окончательно получим |
|||||||||||||||||
|
|
dt |
|
dt2 |
|
|
|
|||||||||||||||||||||||||
|
d3x |
|
d2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
dx |
x 0. |
Решим |
это |
уравнение. |
|
Соответствующее |
ему |
|||||||||||||||||||||
|
dt3 |
dt2 |
|
dt |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 k 1 0 |
|
|
|
|
|||||||||
характеристическое уравнение k3 k2 k 1 k2 |
|
имеет корни |
||||||||||||||||||||||||||||||
k |
1, |
k |
2,3 |
i. Следовательно, |
x C et |
C |
2 |
|
cost C |
3 |
sint. |
Функции y и |
||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
z |
|
в |
соответствии |
с соотношениями |
|
y |
dx |
|
|
и z |
d2x |
|
после |
||||||||||||||||||
|
|
|
dt |
|
dt2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
дифференцирования |
полученного |
для |
|
|
|
x |
|
|
|
выражения |
имеют |
вид: |
||||||||||||||||||||
yC1et C2 sint C3 cost и x C1et C2 cost C3 sint.
3.2.Решение систем дифференциальных уравнений с помощью характеристического уравнения
Пусть дана однородная система
dx
dt a1x b1y c1z,dy
a2x b2 y c2z,dzdt a3x b3y c3z,
dt
где ai, |
bi, ci - постоянные. Будем искать частные решения системы в виде |
||||||||
x r ekt, |
y r ekt, |
z r ekt |
, где |
r , r |
, r и k - неопределенные |
||||
1 |
2 |
|
|
3 |
|
1 |
2 |
3 |
|
коэффициенты, которые следует найти. Уравнение |
|||||||||
|
a1 k |
b1 |
|
c1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
a2 |
b2 k |
|
c2 |
0 |
|
|
|
|
|
a3 |
b3 |
c3 k |
|
|
|
|
|
|

90
называется характеристическим уравнением системы. Отыскав корни этого уравнения, и поочередно подставляя их в исходную систему, определим коэффициенты r1, r2, r3.
Пример. Найти общее решение системы
dx
dt z,dy
4x y 4z,
dzdt y.
dt
Решение. Система в данном случае имеет вид:
Характеристическое
kr1 r3 0,
4r1 1 k r2 4r3 0, r2 kr3 0.
уравнение
|
k |
|
0 |
|
|
1 |
|
k3 |
k2 4k 4 4 k2 k 1 0 |
|
|
имеет |
|
корни |
|||||||||||||||||||||
|
4 |
1 k |
4 |
|
|
|
|
||||||||||||||||||||||||||||
|
0 |
|
1 |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1, |
k |
|
2, |
k |
|
2. |
Для |
k |
1 |
|
r |
r 0, |
|
|
Решением |
|
этой |
||||||||||||||||||
|
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|||||||||||||||||||||||
1 |
|
|
2 |
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
|
|
r2 r3 0. |
|
|
|
|
|
|
|
|
||||||||
системы будут, например, |
числа |
r |
1 |
1, |
|
r |
1 |
1, |
r |
1 |
1 |
(здесь |
r 1 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|||
выбрано произвольно). |
Следовательно, |
x |
e t , |
y |
|
|
e t , z |
e t . |
Для |
||||||||||||||||||||||||||
|
|
|
2r1 r3 0, |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|||||||
k1 2 |
|
|
|
Решая |
|
|
|
|
эту |
|
|
|
систему, |
|
|
получим |
|||||||||||||||||||
2r 2r |
0. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
r 2 |
|
|
2 |
2 |
|
3 |
|
2 |
|
|
|
|
|
|
|
|
e 2t , |
|
|
|
4e 2t , |
|
|
2e 2t . |
|||||||||||
1, |
r |
4, |
r |
2; |
тогда |
|
|
x |
2 |
y |
2 |
z |
2 |
||||||||||||||||||||||
1 |
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Наконец, |
|
|
для |
|
k3 2 |
2r1 r3 0, |
|
|
|
Здесь |
|
|
|
можно |
|
положить |
|||||||||||||||||||
|
|
|
r 2r |
|
0. |
|
|
|
|
|
|
|
|||||||||||||||||||||||
r 3 |
|
r 3 |
|
|
|
|
3 2 |
|
2 |
3 |
|
|
|
|
|
|
e2t , |
|
|
|
|
4e2t |
|
|
|
|
2e2t . |
||||||||
1, |
4, |
r |
и будем иметь |
x |
3 |
|
|
y |
3 |
, |
|
z |
3 |
||||||||||||||||||||||
1 |
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Общее решение данной системы дифференциальных уравнений таково:
x C1e t C2e 2t C3e2t ,
y C1e t 4C2e 2t 4C3e2t ,.
zC1e t 2C2e 2t 2C3e2t.
Пример. Решить систему
dx
dt 7x y,dy 2x 5y.
dt
Решение. Чаще системы дифференциальных уравнений записывают в виде:
