36

Ч а с т ь I I

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ЛАБОРАТОРНЫМ РАБОТАМ

1. М Е Х А Н И К А

Работа 1.1

ИЗУЧЕНИЕ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ УСКОРЕНИЯ

СВОБОДНОГО ПАДЕНИЯ С ПОМОЩЬЮ МАТЕМАТИЧЕСКОГО МАЯТНИКА

Цель работы:   1) изучение колебаний математического маятника: измерение периода его колебаний и определение ускорения свободного падения;

2) оценка случайной и приборной погрешностей измерения; изучение зависимости ширины доверительного интервала от числа опытов и доверительной вероятности.

С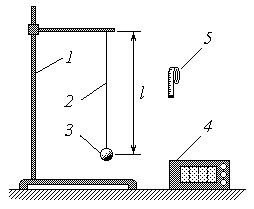хема экспериментальной установки

1 – штатив;

2 – нить длиной l;

3 – груз;

4 – секундомер;

5 – сантиметровая лента

Описание методики измерений

Известно, что математический маятник представляет собой небольшой массивный груз, подвешенный на длинной легкой нити. При малых углах отклонения нити от вертикали колебания груза близки к гармоническим и их период Т определяется формулой

, (1)

где l – длина нити; g – ускорение свободного падения. Выразим из формулы (1) величину g:

. (2)

Таким образом, измерив длину нити и период колебаний маятника, можно опытным путем найти ускорение свободного падения. Для получения более точного результата следует измерять не время одного полного колебания (период) Т, а время нескольких (N) колебаний t. Учитывая, что , преобразуем выражение (2) к виду

. (3)

Из формулы (1) следует, что при фиксированной длине нити l период колебаний маятника Т представляет собой постоянную величину (g = const для данной географической точки). Поэтому при неоднократном измерении времени t одного и того же количества N колебаний, казалось бы, должен получаться неизменный результат. Однако даже при использовании сравнительно точного прибора (например, электронного секундомера) можно убедиться в том, что от опыта к опыту значение t изменяется то в большую, то в меньшую сторону. Различия в результатах измерения одной и той же величины объясняются случайными погрешностями. Изучение погрешностей является одной из главных целей данной лабораторной работы.

Если при многократных измерениях количество колебаний N брать неизменным, то расчетную формулу (3) для определения ускорения свободного падения удобнее представить в виде

  , (4)

где

 C = (2 N)² l   . (5)

Порядок измерений и обработки результатов

Упражнение 1. ОЦЕНКА ПОГРЕШНОСТЕЙ РЕЗУЛЬТАТА 25 ИЗМЕРЕНИЙ

1. С помощью сантиметровой ленты измерьте длину нити l, т.е. расстояние от точки подвеса до центра тяжести груза. Выразив величину l в метрах, по формуле (5) рассчитайте константу С (значение N указывается преподавателем). Запишите полученный результат (в метрах) в тетрадь.

2. Под руководством преподавателя или лаборанта научитесь работе с секундомером.

3. Выведите маятник из положения равновесия и отпустите, наблюдая начавшиеся колебания. Помните, что максимальный угол отклонения нити от вертикали при этом должен быть малым (примерно в пределах 10). Следите за тем, чтобы колебания маятника происходили в вертикальной плоскости (груз не должен описывать круги или «восьмерки»).

4. Не останавливая колебаний маятника, для тренировки несколько раз измерьте время t, в течение которого он совершает N полных колебаний. Сообщите результаты измерений преподавателю или лаборанту.

5. С разрешения последних приступайте к выполнению основной части работы. Повторив описанные выше измерения 25 раз, заполните первые два столбца табл. 1.

Таблица 1

Номер опыта	t, c	g, м/с2	 g, м/с2	( g)2, (м/с2)2
1
2
…	…	…	…	…
25
	 =		 =

6. Для каждого опыта рассчитайте ускорение свободного падения по формуле (4); результаты расчетов занесите в третий столбец табл. 1.

7. Изучите методику оценки случайной и приборной погрешностей измерения (см. часть I, с. 6-18).

8. Вычислите сумму полученных значений величины g и занесите результат в соответствующую ячейку таблицы. Рассчитайте среднее значение и запишите его в тетрадь.

9. Для каждого i-го опыта найдите отклонение значения от среднего , а также квадрат отклонения (g_i)². Результаты расчетов занесите в два последних столбца табл. 1.

10. Рассчитайте сумму квадратов отклонений и запишите ее в соответствующую ячейку. Вычислите среднеквадратичную ошибку .

11. Выберите из таблицы на с. 149 значение коэффициента Стьюдента t_n, для n = 25 опытов и доверительной вероятности  = 0,95. Рассчитайте и запишите в тетрадь случайную погрешность измерения _s g.

12. Определите абсолютные приборные погрешности прямых измерений длины нити  l и времени  t ; оцените относительные ошибки Запишите полученные значения в тетрадь и сравните их между собой.

13. Оцените абсолютную приборную погрешность косвенного измерения ускорения свободного падения  g. При необходимости используйте формулу

.

14. Оцените полную абсолютную  и относительную Е ошибки. Приведите точность вычисления среднего значения в соответствие с найденной погрешностью. Запишите окончательный результат измерений.

Упражнение 2. ОЦЕНКА ПОГРЕШНОСТЕЙ РЕЗУЛЬТАТА 5 ИЗМЕРЕНИЙ

1. По указанию преподавателя выберите из табл. 1 пять значений ускорения свободного падения g и перепишите их во второй столбец табл. 2.

Таблица 2

Номер опыта	g, м/с2	 g, м/с2	( g)2, (м/с2)2
1
2
…	…	…	…
5
 =		 =

2. Выполните пп. 8, 9, 10 упражнения 1.

3. Для доверительной вероятности  = 0,95 и числа опытов п = 5 оцените случайную погрешность измерения _s g.

4. Используя найденное в пп. 12 и 13 первого упражнения значение абсолютной приборной ошибки  g, найдите полную погрешность измерений и запишите окончательный результат.

5. Повторите пп. 3 и 4 упражнения 2 для другого значения доверительной вероятности  (указывается преподавателем).

6. По результатам проведенных измерений и расчетов сделайте выводы.

Контрольные вопросы

1. Абсолютная и относительная ошибки измерений.

2. Случайная и приборная погрешности.

3. Оценка случайной ошибки. Доверительный интервал.

4. Способы определения приборных ошибок.

5. Погрешности косвенных измерений.

6. Полная ошибка. Запись окончательного результата измерений.