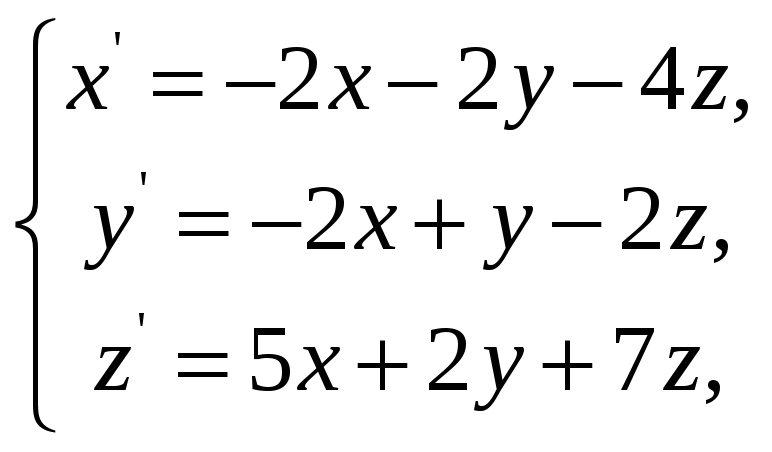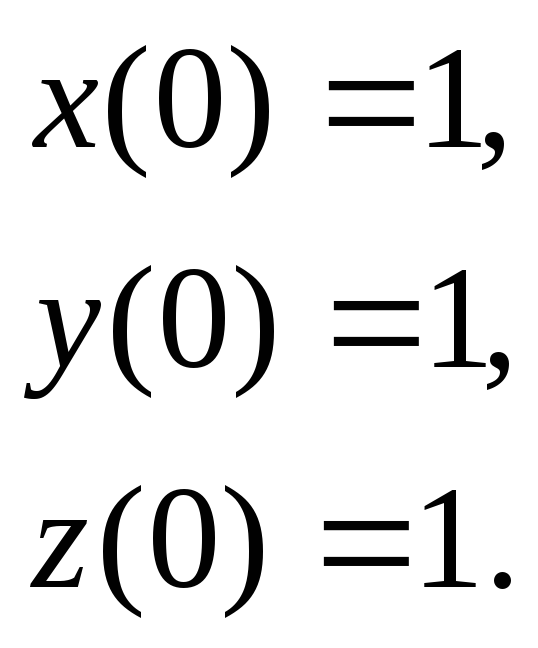математика

Операционное исчисление

Преобразование Лапласа.

Рассмотрим функцию действительного переменного , определенную при . Будем также считать, что функция - кусочно-непрерывная, т.е. в любом конечном интервале она имеет конечное число точек разрыва первого рода, и определена на бесконечном интервале , но при .

Будем считать, что функция ограничена условием:

Рассмотрим функцию

где – комплексное число.

Определение. Функция называется изображением Лапласа функции .

Также функцию называют – изображением или преобразованием Лапласа.

Обозначается

При этом функция называется начальной функцией или оригиналом, а процесс нахождения оригинала по известному изображению называется операционным исчислением.

Теорема. (Теорема единственности) Если две непрерывнные функции и имеют одно и то же – изображение , то они тождественно равны.

Определение. Функцией Хевисайда называется функция

Таблица изображений некоторых функций.

Для большинства функций изображение находится непосредственным интегрированием.

Пример. Найти изображение функции .

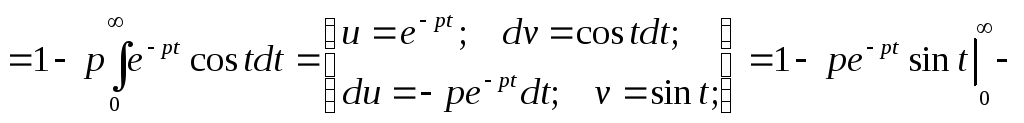
Для многих функций изображения посчитаны и приведены в соответствующих таблицах.

№	f(t)	F(p)	№	f(t)	F(p)
1	1		5
2			6
3			7
4			8

Свойства изображений.

Если , то справедливы следующие свойства:

1) Свойство подобия.

Пример.

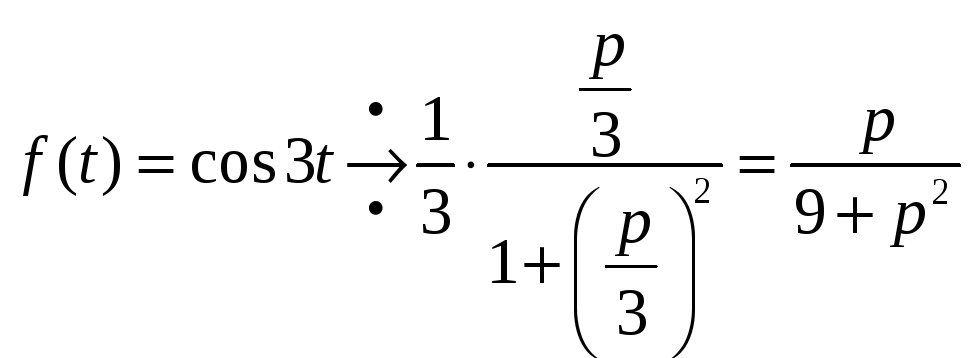
2) Свойство линейности.

Пример.

3) Смещение изображения.

Пример.

4) Дифференцирование изображения.

Пример.

5) Дифференцирование оригинала.

6) Интегрирование изображения.

(Справедливо при условии, что интеграл сходится)

Пример.

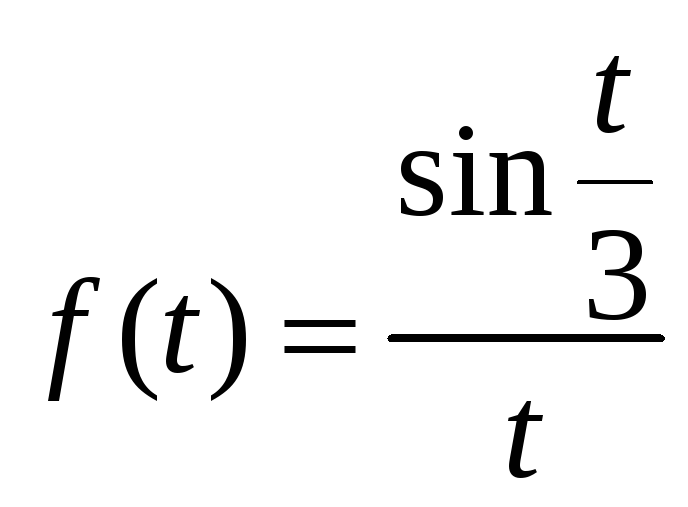
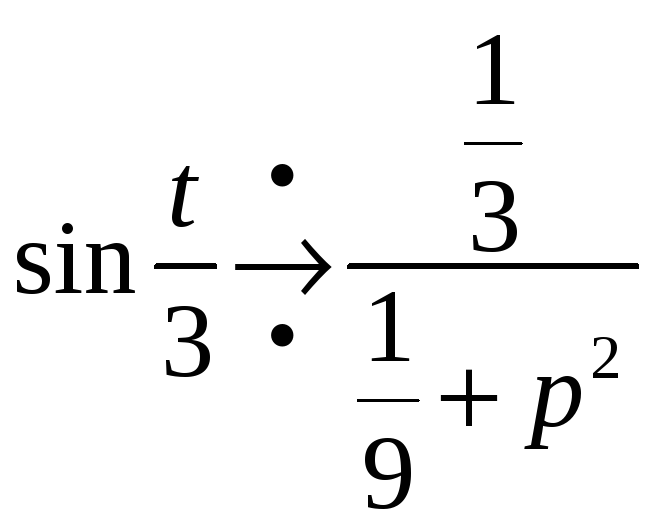
7) Интегрирование оригинала.

Пример.

Теоремы свертки и запаздывания.

Теорема. (теорема запаздывания) Если f(t) = 0 при t < 0, то справедлива формула

где t₀ – некоторая точка.

Пример.

Определение. Выражение называется сверткой функций f₁(t) и f₂(t) и обозначается f₁ f₂.

Теорема. (теорема свертки) Преобразование Лапласа от свертки равно произведению преобразований Лапласа от функций f₁(t) и f₂(t) .

Теорема. (Интеграл Дюамеля). Если , то верно равенство

Для нахождения изображений различных функций наряду с непосредственным интегрированием применяются приведенные выше теоремы и свойства.

Пример. Найти изображение функции .

;

Восстановление оригинала по данному изображению

Решение задач на отыскание оригиналов по их изображениям вызывает определенные трудности, так как при этом необходимо использование таблиц изображений в «обратном» порядке, что требует в свою очередь некоторой изобретательности. Как правило, данное изображение путем тех или иных алгебраических преобразований приводится к «табличному» изображению или сумме «табличных» изображений. При этом, в случае необходимости, используются: простейшие теоремы операционного исчисления; смещения и запаздывания; известный метод разложения правильной рациональной дроби на сумму простейших дробей.

Примеры

1.

;

.

2.

,

По теореме запаздывания: .

3. .

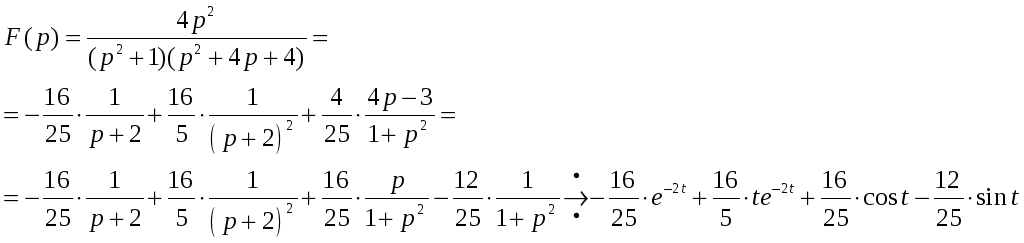4.

;

Теорема разложения

Теорема: Если изображение функции представляет собой дробь , знаменатель которой имеет только простые корни , то оригинал имеет следующий вид: .

Операционное исчисление используется как для нахождения значений интегралов, так и для решения дифференциальных и интегральных уравнений.

Пусть дано линейное дифференциальное уравнение с постоянными коэффициентами.

Требуется найти решение этого дифференциального уравнения, удовлетворяющее начальным условиям:

Если функция является решением этого дифференциального уравнения, то оно обращает исходное уравнение в тождество, значит функция, стоящая в левой части уравнения и функция имеет (по теореме единственности) одно и то же изображение Лапласа.

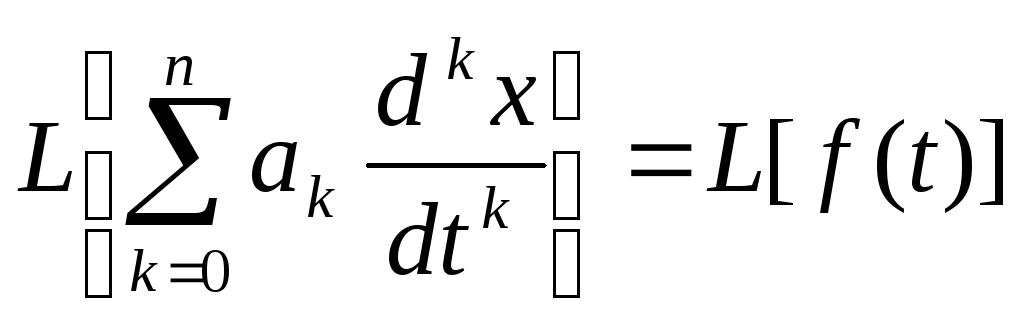
Из теоремы о дифференцировании оригинала {} можно сделать вывод, что

Тогда

Обозначим

Получаем:

Это уравнение называется вспомогательным (изображающим) или операторным уравнением.

Отсюда получаем изображение , а по нему и искомую функцию x(t).

Изображение получаем в виде:

Где

Этот многочлен зависит от начальных условий. Если эти условия нулевые, то многочлен равен нулю, и формула принимает вид:

Рассмотрим применение этого метода на примерах.

Пример. Решить уравнение

Изображение искомой функции будем искать в виде:

Находим оригинал, т.е. искомую функцию:

Контрольная работа №1

(номер варианта определяется по последней цифре номера зачетной книжки)

Задача 1. Найти функции-изображения для данных функций-оригиналов.

1.1. .

1.2. .

1.3.

1.4.

1.5.

1.6.

1.7.

1.8.

1.9.

1.10.

Задача 2. По данных функций-изображений найти функции-оригиналы.

2.1. ; .

2.2. ;

2.3. ; .

2.4. ; .

2.5. ; .

2.6. ;

2.7. ; .

2.8. ;

2.9. ; .

2.10. ;

Задача 3. Решить дифференциальное уравнение и систему дифференциальных уравнений методом операционного исчисления.

3.1. ;

3.2. ;

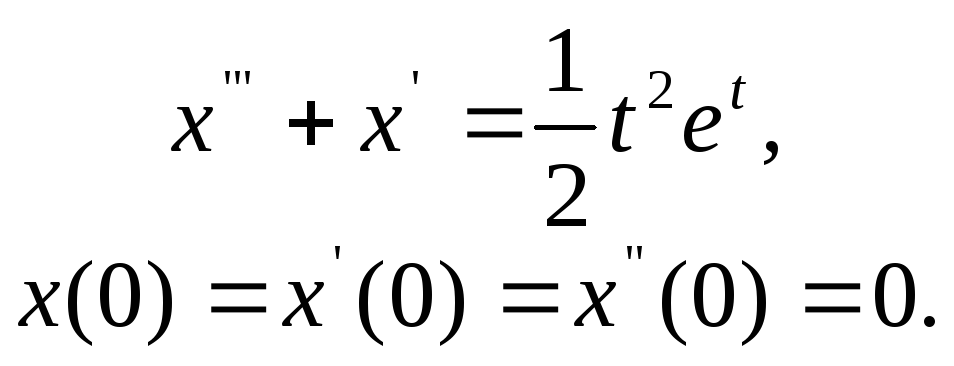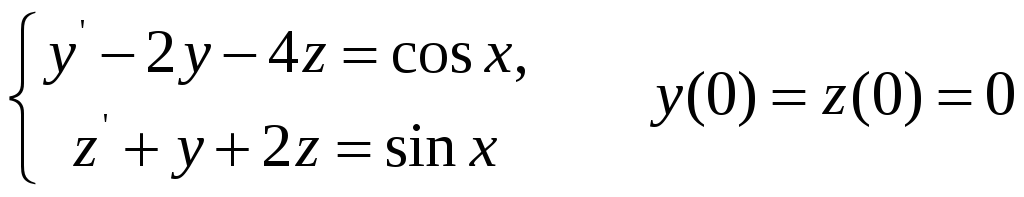
3.3. ;

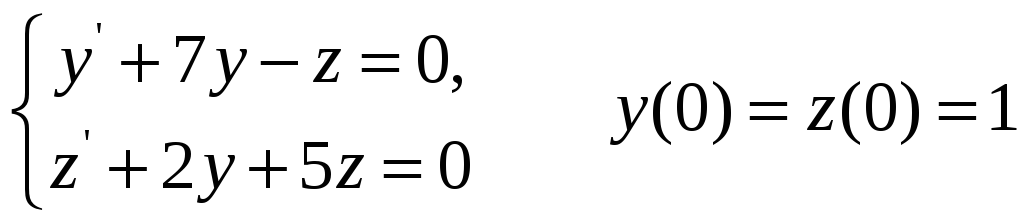
3.4. ;

3.5. ;

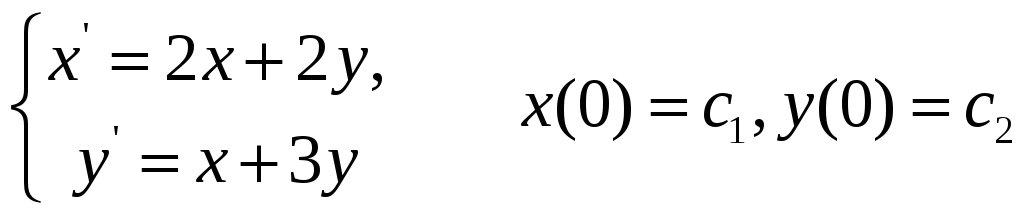
3.6. ;

3.7. ;

3.8. ;

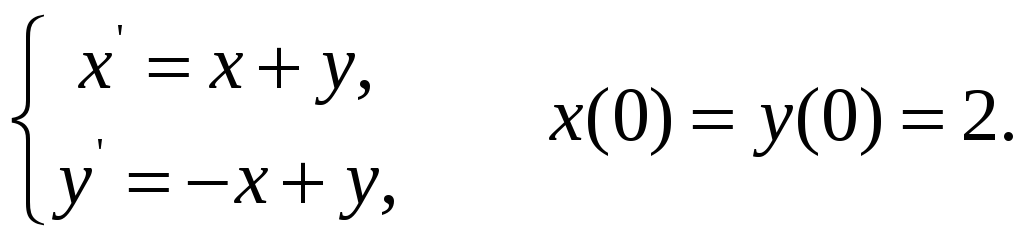
3.9. ;

3.10. ;

7