4. Асимптоты графика функции

Пусть M(x, y)  точка графика функции y=f(x). Будем говорить, что точка M бесконечно удаляется в бесконечность по графику, если она движется по графику так, что либо x → ± ∞, либо y→ ± ∞. При этом считаем, что функция определена в соответствующих множествах.

Прямая называется асимптотой графика функции y = f(x), если при удалении точки M в бесконечность по графику, расстояние от M до этой прямой стремится к нулю (рис. а).

Вертикальная (горизонтальная) асимптота  это асимптота, параллельная оси Оу (соответственно Ох). Остальные асимптоты называются наклонными.

На рис. б и в прямые х = 2, х = 0 и х = 1 являются вертикальными асимптотами, прямая у = 1  горизонтальной, прямая у = х+2  наклонной.

Нахождение вертикальных асимптот

Если x₀ точка бесконечного разрыва функции y = f(x), то прямая x = x₀ является вертикальной асимптотой. Например, если

то точка графика при y → ∞ бесконечно близко приближается к вертикальной асимптоте x = x₀ с левой стороны (рис. 6в, x₀= 1).

Рис. 12

Вертикальная асимптота может быть в точке, являющейся границей области определения функции, если односторонний предел в этой точке равен +∞ или ∞ (рис. в).

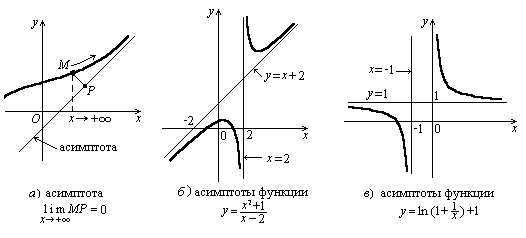
Нахождение горизонтальных асимптот

Если приx →+ ∞ (или ∞), то прямая y = y₀ является горизонтальной асимптотой при x →+ ∞ (или ∞).

Нахождение наклонных асимптот

Уравнение наклонной асимптоты имеет вид y= kx+b , где угловой коэффициент k ≠ 0. Коэффициенты k и b при x →+∞ (∞) находят по формулам:

.

Замечание

В этих формулах подразумевается, что оба предела существуют и конечны. Если хотя бы один из них не существует, то наклонной асимптоты нет.

Замечание

Если пределы конечны и k = 0, то график имеет горизонтальную асимптоту y= b при x →+ ∞ (или ∞). Поэтому если существует горизонтальная асимптота при x →+ ∞ (или ∞), то нет наклонной асимптоты при x →+ ∞ (или ∞).

Типовые примеры

Найти асимптоты графика функции.

1) .

►Точка x = 2 является точкой разрыва функции. Найдем односторонние пределы функции в этой точке

Следовательно, прямая x = 2 является вертикальной асимптотой при у→ + ∞ и у→ ∞.

Так как то горизонтальных асимптот нет.

Найдем наклонные асимптоты:

, следовательно, прямая у = х+2 является наклонной асимптотой при x →  ∞ (рис. б). ◄

2)

►Областью определения функции является множество всех решений неравенства Решим его:. Найдем односторонние пределы в границах области определениях = 1 и х = 0:

.

Следовательно, прямая x = 1 является вертикальной асимптотой при у→  ∞, а прямая x = 0 является вертикальной асимптотой при у→ +∞ (рис. в).

Так как то прямаяу = 1 является горизонтальной асимптотой при x → ∞ (рис. в). Наклонных асимптот нет. ◄

Пример

Функция полных издержек (функция затрат, кривая «затраты-выпуск») однопродуктовой фирмы задана уравнением . Здесь‑ объем выпуска продукции,‑ соответствующие издержки производства. При каком объеме производства средние издержки минимальны?

►Средние издержки равны полным затратам, отнесенным на единицу продукции, то есть в данном случае

.

Как видим, графиком функции средних издержек является гипербола с наклонной асимптотой. При этом минимум функции средних издержек определяется из условия , откуда получаем

,

Стационарная точка - . Вторая производная функции средних издержек . В точке значение второй производной функции средних издержек положительно, следовательно, в точке исследуемая функция имеет минимум.◄

Пример

Функция полных издержек однопродуктовой фирмы задана уравнением . Цена товара на рынке равна 12. Определить область безубыточности. При каком объеме производства фирма получит максимальную прибыль, если весь товар находит покупателя?

►Прибыль фирмы определяется как разность между доходом (выручкой от продажи) и полными издержками:

.

Поскольку цена продукции постоянна, то , вследствие чего графиком функции прибыли является парабола, ветви которой направлены вниз:

.

Область безубыточности определяется из решения неравенства . Так как корнями квадратного трехчлена, стоящего в левой части неравенства, являются числа и , то областью безубыточности является интервал . Итак, при прибыль фирмы положительна. Найдем теперь значение объема выпуска продукции, при котором прибыль достигает своего максимального значения. Из необходимого условия экстремума получаем, т.е.. Так как, то- точка максимума. ◄

Пример

Функция полных издержек однопродуктовой фирмы задана уравнением . Цена товара на рынке равна 12. Определить область безубыточности, если с каждой единицы товара фирма выплачивает в бюджет налог в размере . Определить, при каком наибольшем целом значении налоговой ставки производство продукции может быть прибыльным.

►Прибыль фирмы после налогообложения определяется как разность между доходом (выручкой от продажи), полными издержками и отчислениями в бюджет: .

Графиком функции прибыли является парабола, ветви которой направлены вниз:

.

Здесь ‑ корни квадратного трехчлена. Поэтому теперь область безубыточностизависит от значения параметра. Заметим, что при из полученных формул следует. Если ставка налога начинает увеличиваться, то тоже начинает расти, а  – уменьшается. Более того, интервал лежит в положительной области лишь при значениях налоговой ставки. Прифункции прибыли после налогообложения имеет вид

.

Поэтому наибольшее целое значение налоговой ставки, при котором производство продукции является прибыльным, равно . В этом случае максимум прибыли достигается при; выручка от продажи равна; издержки производства составляют; отчисления в бюджет равны. Поэтому прибыль после налогообложения составит. Как видим, отчисления в бюджет при налоговой ставкеболее чем в 8 раз превышают прибыль фирмы после налогообложения. ◄

Пример

Функция спроса от дохода М имеет вид . Исследовать данную функцию.

►Данная функция спроса представляет собой монотонно возрастающую экспоненциальную функцию, поскольку ее производнаядля всех. Функция имеет горизонтальную асимптоту, поскольку . График выпуклый вверх, т.к. для всех.◄

Пример

По оценке социологов во время предвыборной кампании в городе число приверженцев кандидата на пост мэра () увеличивается во времени (- недели) согласно уравнению . Когда ежедневный прирост приверженцев кандидата начнет спадать? Оценить максимальное число его сторонников накануне выборов.

►Ежедневный прирост сторонников кандидата напрямую зависит от скорости роста его приверженцев . Поскольку

,

функция является монотонно возрастающей, причем при скорость роста приверженцев растет, а при‑ падает. Это означает, что график функциипри выпуклый вниз, а при ‑ выпуклый вверх. Таким образом, через, т.е. на пятой неделе, популярность кандидата начнет спадать. Поскольку функция имеет горизонтальную асимптоту, а время выборов в задаче не указано, то число приверженцев кандидата накануне выборов не превысит 10000. Отметим, что точка с координатами является точкой перегиба графика функции.◄