
- •Глава . Производная и ее применение
- •§1. Производная функции
- •1. Определение производной
- •2. Действия над дифференцируемыми функциями
- •4. Производная функции, заданной параметрически
- •5. Дифференцирование показательно-степенной функции
- •6. Производные высших порядков
- •8. Теоремы Ферма, Ролля, Коши и Лагранжа
- •10. Формула Тейлора
- •10.1. Формула Тейлора для многочленов
- •10.2. Формула Тейлора для произвольной функции
- •10.3. Форма Пеано остаточного члена формулы Тейлора
- •10.4. Форма Лагранжа остаточного члена формулы Тейлора
- •10.5. Представление по формуле Маклорена элементарных функций
- •11. Формула Тейлора и эквивалентные бесконечно малые. Вычисление пределов с помощью формулы Тейлора
- •12. Приближённые вычисления с помощью формулы Тейлора
- •§2. Исследование поведения функций и ее построение ее графика
- •1. Промежутки монотонности функции
- •2. Экстремумы функции
- •3. Направление выпуклости функции. Точки перегиба
- •4. Асимптоты графика функции
- •Так как то горизонтальных асимптот нет.
- •5. Исследование функции и построение ее графика
- •Вопросы промежуточного контроля
12. Приближённые вычисления с помощью формулы Тейлора
Ранее мы пользовались выражением у(x+х) у(x)+ у'(x) х, которое, как теперь очевидно, содержит два первых члена формулы Тейлора. Формула Тейлора обобщает это выражение; она позволяет проводить более точные вычисления и оценивать точность этих вычислений.
Типовой пример
Требуется вычислить sin1 с погрешностью, не превышающей 0,00001.
►Остаточный
член в форме Лагранжа для функции
![]() имеет вид
имеет вид![]() ,
следовательно
,
следовательно
![]() .
Подбором находим, что
.
Подбором находим, что![]() ,
следовательно, мы должны взять степених
вплоть до седьмой:
,
следовательно, мы должны взять степених
вплоть до седьмой:
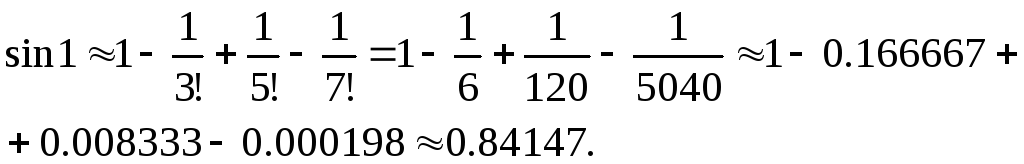 ◄
◄
§2. Исследование поведения функций и ее построение ее графика
1. Промежутки монотонности функции
Функция
![]() называетсявозрастающей
(убывающей)
в промежутке
называетсявозрастающей
(убывающей)
в промежутке
![]() из области определения, если для любых
из области определения, если для любых![]() из условия
из условия![]() следует неравенство
следует неравенство![]() (соответственно
(соответственно![]() ).
).
На рисунке 2а функция возрастает в интервалах (a, b), (c, d), убывает в (b, c ).
Под монотонностью понимается либо возрастание, либо убывание.
ТЕОРЕМА
(достаточное условие монотонности).
Если функция f(x)
дифференцируема в промежутке
![]() и f (x)>0
( f (x)<0
) для всех
и f (x)>0
( f (x)<0
) для всех
![]() ,
тоf(x)
возрастает (соответственно убывает) в
промежутке X.
,
тоf(x)
возрастает (соответственно убывает) в
промежутке X.
2. Экстремумы функции
Точка x0 называется точкой минимума (максимума) функции y=f(x), если она определена в некоторой окрестности этой точки и для каждой точки x ≠x0 этой окрестности f(x) > f(x0) (соответственно f(x) < f(x0)). Значение функции f(x0) называется минимумом (соответственно максимумом).
На рисунке 7а точка b – точка минимума, точка c – точка максимума. Под экстремумом понимается либо минимум, либо максимум.
Точка x0 из области определения функции y=f(x), называется критической точкой, если либо f(x) дифференцируема в x0 и f (x0) = 0, либо f(x) не дифференцируема в x0. На рис. 7б и в точка x0 – критическая.
Рис.
7

f (x), то она является критической точкой этой функции.
На рис. 7б критическая точка x0 является точкой экстремума, а на рис. 7в критическая точка x0 не является точкой экстремума. Таким образом, не всякая критическая точка является точкой экстремума.
Первое достаточное строгого условие экстремума
Пусть x0 критическая точка функции y=f(x). Если в некоторой окрестности точки x0 слева от нее производная f (x) принимает один знак, а справа от нее противоположный, то x0 точка экстремума. При этом если слева f’(x)>0, справа f (x)<0, то x0 точка максимума, в противном случае x0 точка минимума. Если в некоторой проколотой окрестности точки x0 производная f (x) принимает один знак, то x0 не является точкой экстремума. Если к тому же f (x) непрерывна в x0, то функция монотонна в этой окрестности.
Второе достаточное условие строгого экстремума
Пусть f (x0)=0 и существует f′′( x0). Тогда если f ′′( x0)>0, то x0 точка максимума. Если же f ′′( x0)<0, то x0 точка минимума.
Этим достаточным условием экстремума удобно пользоваться, если достаточно сложно установить знак первой производной в окрестности точки экстремума.
Третье достаточное условие строгого экстремума
ТЕОРЕМА.
Пусть функция
![]() имеет в точке
имеет в точке
![]() все производные вплоть до n-го
порядка, причём
все производные вплоть до n-го
порядка, причём
![]()
![]() .
Тогда, еслиn
(порядок первой отличной от нуля
производной) нечётно, то экстремум в
точке
.
Тогда, еслиn
(порядок первой отличной от нуля
производной) нечётно, то экстремум в
точке
![]() отсутствует; если
n
чётно, то при
отсутствует; если
n
чётно, то при
![]()
![]() - точка минимума, при
- точка минимума, при
![]()
![]() - точка максимума.
- точка максимума.
Правило нахождения точек экстремума и промежутков монотонности
1) Найти область определения функции f(x).
2) Найти все критические точки функции f(x). Для этого найти производную, решить уравнение f (x)=0 и найти точки x из области определения, в которых f (x) не существует.
3) Разбить область определения критическими точками на промежутки и в них найти знаки производной.
4) В промежутках, где производная положительна, функция возрастает, а в промежутках, где производная отрицательна, функция убывает.
5) Точки экстремума ищем среди критических точек. Пусть x0 – критическая точка. Если в интервале слева от x0 производная положительна (отрицательна), а справа отрицательна (положительна), то x0 точка максимума (минимума).
Замечание
Если в интервале слева и справа от x0 производная имеет один и тот же знак, то x0 не является точкой экстремума. При этом, если функция непрерывна в этой точке, то функция монотонна в целом в этих двух интервалах.
Рис.
8
Исследовать
функцию
![]() на экстремум и монотонность.
на экстремум и монотонность.
►1) Область определения – множество всех действительных чисел R.
2)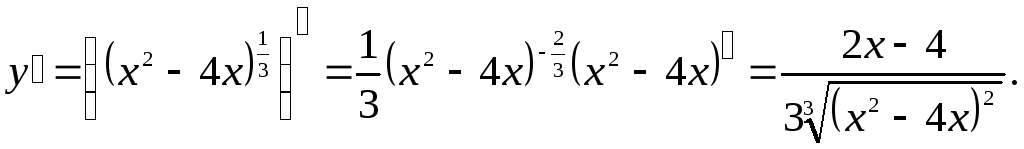
Найдем
критические точки. Решим уравнение y
= 0:
![]() критическая.
y
не существует
при
критическая.
y
не существует
при
![]() x (x
– 4) = 0
x (x
– 4) = 0
![]() x
= 0 или
x
= 0 или
![]() .
Эти точки входят в область определения
функции, следовательно, являются
критическими.
.
Эти точки входят в область определения
функции, следовательно, являются
критическими.
3)
Разобьем область определения R
критическими точками 0, 2, 4 на интервалы
(– ∞, 0), (0, 2), (2, 4), (4, +∞), в каждой из
которых производная сохраняет знак.
Найдем знаки производной в этих
интервалах. Для этого выберем по одной
точке из этих интервалов (например,
–1![]() (–
∞, 0), 1
(–
∞, 0), 1![]() (0,
2), 3
(0,
2), 3![]() (2,
4), 5
(2,
4), 5![]() (4,
+∞)) и определим знаки производной
y
в этих точках: y(1)
< 0, y(1)
< 0, y(3)
> 0, y(5)
> 0. Следовательно, y
< 0 в интервалах (– ∞, 0), (0, 2) и y
> 0 в интервалах (2, 4), (4, +∞).
(4,
+∞)) и определим знаки производной
y
в этих точках: y(1)
< 0, y(1)
< 0, y(3)
> 0, y(5)
> 0. Следовательно, y
< 0 в интервалах (– ∞, 0), (0, 2) и y
> 0 в интервалах (2, 4), (4, +∞).
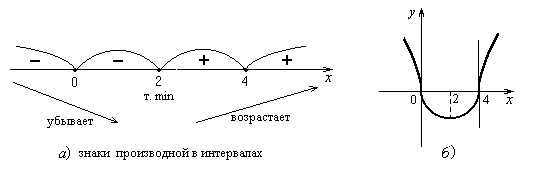
4) Функция убывает в интервалах (– ∞, 0) и (0, 2), возрастает в интервалах (2, 4) и (4, +∞). Однако можно сделать более сильный вывод. В самом деле, в окрестностях критических точек x = 0 и x = 4 производная не меняет знака, значит, они не являются точками экстремума. В силу замечания функция убывает в интервале (– ∞, 2) и возрастает в интервале (2, +∞). Заметим, что y(0) = – ∞, y(4) = +∞, следовательно, в точках (0, 0) и (4, 0) касательные параллельны оси Оу.
5) Критическая точка x = 2 является точкой минимума.
На
рисунке изображен схематически график
функции
![]() .◄
.◄
Типовой пример
Найти
наибольшее и наименьшее значения функции
![]() на отрезке [–1; 3].
на отрезке [–1; 3].
►Функция
дифференцируема на всей числовой оси.
Найдём стационарные точки
![]() .
Стационарными точками являютсяx1
= –2, x2
= 0, x3
= 2
; из них
лишь x2
= 0 и x3
= 2 принадлежат промежутку [–1; 3] . Найдём
значения функции в точках x
= 0, x
= 2, а также на концах отрезка: f(0)
= 0, f(2)
= =16 – 32 = –16, f(-1)
= 1 – 8 = –7, f(3)
= 81 – 72 = 9. Сравнив полученные значения,
находим:
.
Стационарными точками являютсяx1
= –2, x2
= 0, x3
= 2
; из них
лишь x2
= 0 и x3
= 2 принадлежат промежутку [–1; 3] . Найдём
значения функции в точках x
= 0, x
= 2, а также на концах отрезка: f(0)
= 0, f(2)
= =16 – 32 = –16, f(-1)
= 1 – 8 = –7, f(3)
= 81 – 72 = 9. Сравнив полученные значения,
находим:
![]() ,
,
![]() .◄
.◄
