10. Формула Тейлора
10.1. Формула Тейлора для многочленов
Рассмотрим
следующую простую задачу. Дан многочлен
по степеням х:
.
Требуется представить функцию Р3(x)
в виде многочлена по степеням (x+2).
Решение: представим х
в виде (х+2)-2.
Тогда
Решим эту задачу по другому:
попытаемся выразить коэффициенты
разложения многочлена по степеням (x+2)
через производные функции Р3(x).
Действительно, если
,
то а0
= Р3
(-2) = 3(-2)3-4(-2)
2+5= -11 (первые
три слагаемых в правом представлении
при подстановке х
= -2 обращаются в нуль). Дифференцируя
Р3(x),
получим
.
Подстановка в это равенство х
= -2 даёт а1
= Р3'(-2)
= 9(-2) 2-4=
32. Находим Р''3
(x):
,
откуда при х
= -2 получим
.
Находим Р3'''(x):
,
откуда
.
Рассмотрим
эту задачу в общем случае: пусть
выразим
коэффициенты этого многочлена через
его производные в точке х0.
Взяв х
= х0,
получим
.
Дифференцируем
:
Следовательно,
.
Находим вторую производную
:
Следовательно,
.
Находим третью производную
:
Следовательно,
.
Далее, находя четвёртую производную,
получим
и т.д. Окончательно:
,i
= 0,1,2,…,n,
и
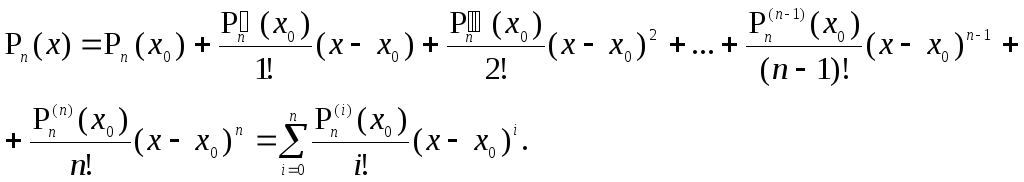
Эта формула и называется формулой Тейлора для многочленов. (Под производной функции f(x) нулевого порядка понимается сама функция f(x); напомним, что 0! = 1 по определению).
10.2. Формула Тейлора для произвольной функции
Пусть теперь f(x) - произвольная функция, которая в точке х0 имеет производные всех порядков до n-го включительно. Построим с помощью производных этой функции многочлен Тейлора n-ой степени:
Значения
этого многочлена и его производных до
n-го
порядка в точке х0
совпадают с производными функции f(x):
=f(x0),
,
однако, если f(x)
- произвольная функция, мы не можем
утверждать, что
;
многочлен
лишь даёт некоторое приближение кf(x).
Разность
называется остаточным
членом формулы Тейлора
и характеризует погрешность этого
приближения. Функция Rn(x)
обладает тем свойством, что и сама Rn(x),
и все её производные вплоть до n-го
порядка в точке х0
равны нулю.
Оценить эту функцию можно различными
способами; мы рассмотрим две наиболее
часто применяемые формы представления
этой функции.
10.3. Форма Пеано остаточного члена формулы Тейлора
Лемма
Пусть
для функции Rn(x)
существуют все производные вплоть до
n-го
порядка и выполняются условия
.
Тогда при
эта функция является бесконечно малой
вышеn-го
порядка по сравнению с х-
х0.
Так
как
,
то
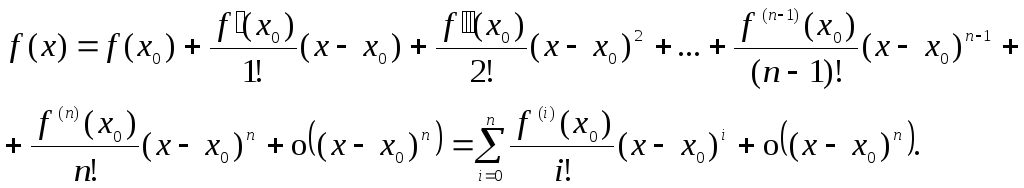
Эта формула называется формулой Тейлора с остаточным членом в форме Пеано.
10.4. Форма Лагранжа остаточного члена формулы Тейлора
Если
в окрестности
точкиx0
существуют все производные функции
f(x)
до n+1-го
порядка, можно получить другое
представление остаточного члена:
,
где
,
точкас
расположена между x
и x0.
Это представление остаточного члена
называется формой
Лагранжа.
Число
с
удобно записать в виде
,
где
,
тогда
.
Итак, формула Тейлора с остаточным членом в форме Лагранжа имеет вид
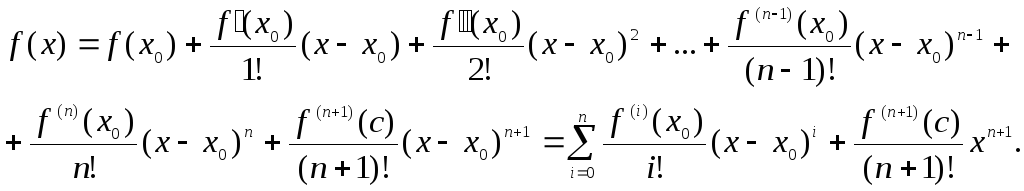
Частный случай формулы Тейлора в случае x0 = 0 принято называть формулой Маклорена. Так, формула Маклорена с остаточным членом в форме Лагранжа такова:
10.5. Представление по формуле Маклорена элементарных функций
Чтобы пользоваться формулой Тейлора, надо знать вид формулы Тейлора (Маклорена) для основных элементарных функций:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Следует
помнить, что применять данные формулы
можно для функции
только в случае, если
при
.
Отметим, что формулы 1-10 можно применять
и в тех случаях, когда данную функцию
требуется представить в виде многочлена
Тейлора по степенямх-х0.
Для этого функцию f(x)
надо преобразовать так, чтобы она
зависела от
,
причем
при
.
Типовые примеры
Разложить по
формуле Тейлора функции в окрестности
точки
:
|
а)
|
б)
|
в)
|
►а)
.
В формуле 1 мы не можем вместох
поставить 3х-2,
так как
при
.
Функцию надо преобразовать:
.
Вместо
х
можно подставить 3х
так как
при
.◄
►б)
.
Сначала преобразуем функцию так, чтобы
первое слагаемое равнялось 1.
Запишем
формулу бинома 6. для случая
.
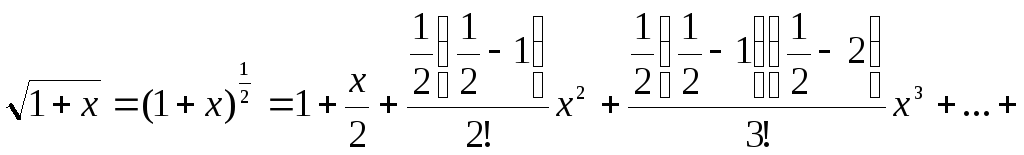
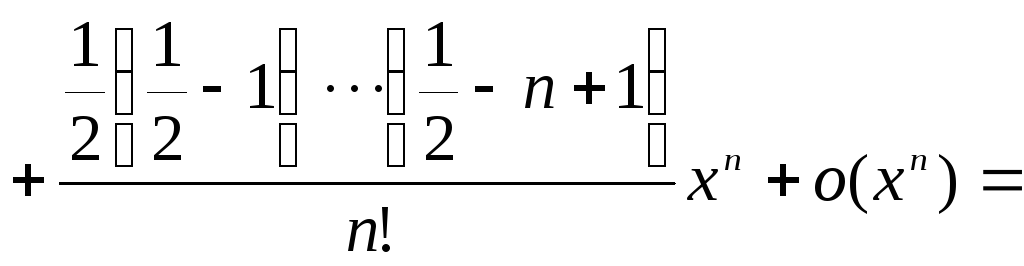
Для
данной функции имеем (вместо х
подставляем
):
.
◄
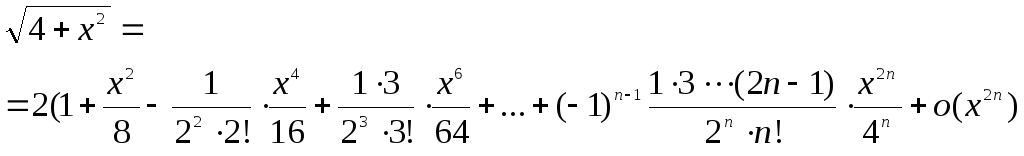►в)
.
Так как здесь
при
,
то можно в формуле 8 вместох
записать
х+6х2.
Однако, если квадратный трехчлен, находящийся под знаком логарифма имеет действительные корни, то лучше разложить его на линейные множители:
.◄
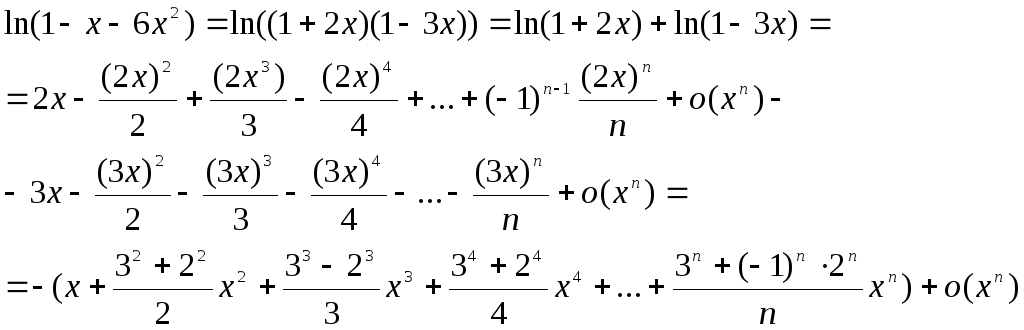Типовые примеры
Представить в виде многочлена Тейлора функции:
|
а)
|
б)
|
по степенямх-1
по степенямх+1 ►а)
по степенямх-1.
Так как
при
,
то использовать формулу 1 пока нельзя.
Надо функцию преобразовать так, чтобы
она зависила от
.
Имеем:
.
Теперь можно использовать формулу 1.
Надо вместо x
подставить 3(x-1).
.◄
►б)
по степенямх+1.
Здесь нам придется применить формулы,
получающиеся из формулы 6 при m
= -1.
.
Сначала данную функцию представим в виде суммы двух простых дробей.
(*)
Каждую дробь надо преобразовать так, чтобы она зависела от (x+1) и первое слагаемое в знаменателе дроби равнялось 1.
.
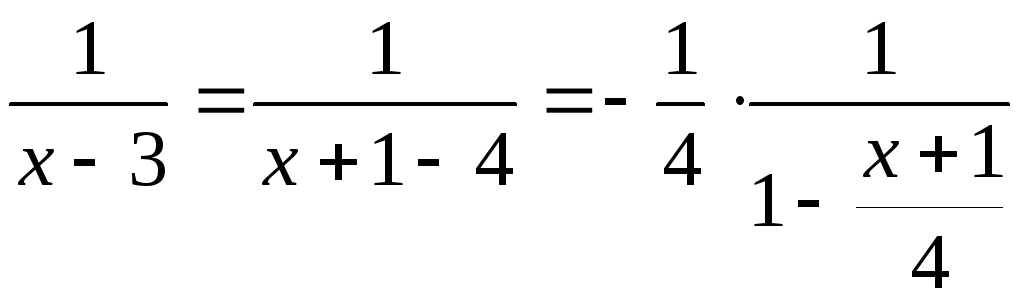Получим:
Для второй дроби имеем:
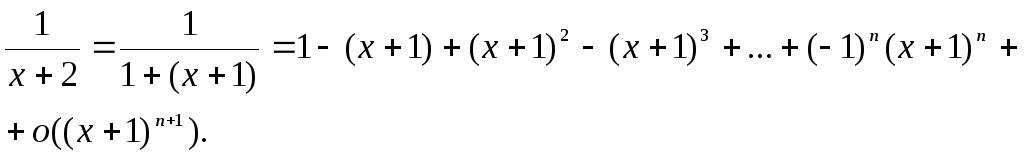
Подставив все это в (*), получим:
.◄