8. Теоремы Ферма, Ролля, Коши и Лагранжа

Функция = достигает в точкелокального максимума, если существует O(,) такая, что    O (,). Аналогично, если    O(,), то функция достигает в точке локального минимума. Локальные максимум и минимум называются локальными экстремумами.

Если функция на отрезке [,], достигает своих наименьшего m и наибольшего М значений, то они могут достигаться в точках локальных экстремумов или на концах отрезка.

ТЕОРЕМА (Ферма). Если функция = имеет производную в точке и достигает в ней локального экстремума, то .

Замечание

В теореме Ферма важно, что х₀ – внутренняя точка для данного промежутка. Например, функция , рассматриваемая на отрезке [0;1], принимает наибольшее и наименьшее значения соответственно при и, но ее производная в этих точках в ноль не обращается.

ТЕОРЕМА (Ролля). Если функция = непрерывна на отрезке [,], дифференцируема на интервале (,), а на концах отрезка принимает равные значения =, то существует по крайней мере одна точка = C, C  (,), в которой (C) = 0.

Следствие

Если функция = непрерывна на [,], дифференцируема на (,) и ()  0   (,), то  .

Замечание

В теореме Ролля существенно выполнение всех трех условий. Приведем примеры функций, для каждой из которых не выполняется только одно из условий теоремы, и в результате не существует такой точки, в которой производная функции равна нулю.

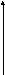
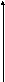у у у

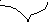
0 1 х 0 х -1 0 1 х

Рис. 4. Рис. 5. Рис. 6.

Действительно, у функции, график которой изображен на рис. 4, , но – точка разрыва, то есть не выполнено первое условие теоремы Ролля. Функция, график которой представлен на рис. 5, не дифференцируема при, а для третьей функции (рис. 6).

Замечание. Геометрический смысл теоремы Ролля: на графике рассматриваемой функции найдется по крайней мере одна точка, касательная в которой параллельна оси абсцисс.

ТЕОРЕМА (Лагранжа). Если функция непрерывна на отрезке и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезканайдется хотя бы одна точка, что

–=

Замечание. Геометрический смысл теоремы Лагранжа: на графике функции найдется точка, касательная в которой параллельна отрезку, соединяющему точки графика с абсциссамии.

ТЕОРЕМА 3 (Коши). Если функции инепрерывные на отрезке [,] и дифференцируемые на интервале (,), причем  0   (,), то найдётся точка = C, C  (,) такая, что

= .

Типовой пример

Показать, что уравнение имеет только один вещественный корень.

►Рассмотрим функцию . Она непрерывна наи имеет производную. Легко видеть, чтопри любых вещественных значениях. Но тогда наше уравнение может иметь не более одного вещественного корня, так как если бы оно имело, например, два корняи, тои по теореме Роля междуинашлась бы такая точка, что. Последнее невозможно. Существование же вещественного корня следует из того, что многочленнечетной степени (любой многочлен нечетной степени с вещественным коэффициентами имеет по крайней мере один вещественный корень).◄

Типовой пример

Из теоремы Лагранжа определите значение для функциина отрезке

►Воспользуемся формулой Лагранжа о конечном приращении: . В данном случае. Подставляя полученные значения в формулу Лагранжа, будем иметь:, откуда, т.е.. Из последнего уравнения определяем значение.◄

Типовой пример

На кривой найти точку, в которой касательная параллельна хорде, соединяющей точкии.

►Рассмотрим функцию на отрезке, концами которого являются абсциссы точеки. На этом отрезке данная функция непрерывна и имеет конечную производную. Следовательно, к ней можно применить теорему Лагранжа. Согласно последней на дугенайдется по крайней мере одна точка, в которой касательная параллельна хорде, причем абсциссой точкибудет значение, удовлетворяющее формуле Лагранжа,

.

Таким образом, решение задачи сводится к определению и. Так как, то, откудаи. Подставляя эти значения в уравнение кривой, найдем. Итак, оказалось, что искомых точек имеется две:и. ◄

Типовой пример

Можно ли к функции применить на отрезке: а) теорему Роля, б) теорему Лагранжа?

►Проверим, удовлетворяет ли данная функция условиям теоремы Роля и Лагранжа. Легко видеть, что непрерывна в каждой точке числовой оси, следовательно, и на отрезке. На концах этого отрезка значения функции совпадают. Что же касается производной, то она не существует в точке. Но точкаявляется внутренней точкой рассматриваемого отрезка. Следовательно, условие существования конечной производной на, требуемое в теоремах Роля и Лагранжа не выполняется. Указанные теоремы к данной функции на отрезкене применимы.◄

Типовой пример

Положим  1 и оценим допущенную при этом ошибку. Для этого рассмотрим функцию = = =,  [ 1; 1,02]. Она удовлетворяет условиям теоремы Лагранжа, поэтому запишем – = (C)  ( 1,02 – 1) = . Очевидно, наибольшая ошибка =– 1 будет приC = 1, т.е.  = 0,004. Итак, если значениемсчитать единицу, то ошибка не превзойдёт 0.004 .

9. Правило Лопиталя. Это правило нахождения некоторых пределов функций при помощи производных. Правило Лопиталя задается следующей теоремой.

ТЕОРЕМА. Пусть: 1) функции f (x) и g(x) дифференцируемы в некоторой проколотой окрестности^* точки а; 2) (или), 3) g(x)  0 и g’(x)  0 в этой окрестности. Тогда, если существует , то существуети верно равенство

.

Замечание

Теорема верна и для случая а =  (+, – ).

Замечание

Теорема верна и для случая

Замечание

Из условий теоремы следует, что функция является неопределенностью видапри, следовательно, теорема позволяет в некоторых случаях раскрыть эти неопределенности.

Замечание

Часто правило Лопиталя применяется повторно следующим образом. Пусть при выполнении условий 1) – 3) теоремы является неопределенностью вида. Тогда правило Лопиталя применяется повторно ки т. д. Если после нескольких повторных применений правила будет получено конечное или бесконечное значение, то оно будет равно.

Типовые примеры

Найти пределы.

1)

►Функции f (x) = e^x – e^-x и g(x) = ln(1+x) удовлетворяют условиям 1) – 3) теоремы, причем имеет место неопределенность вида . Применим правило Лопиталя:

◄

2)

►Имеет место неопределенность вида . Применим правило Лопиталя.

Вновь имеет место неопределенность вида . Следуя замечанию, применим правило Лопиталя повторно. При этом замечаем, что, поэтому правило применяем только к функции:

◄

3)

►Имеет место неопределенность вида . Применим правило Лопиталя.

Здесь правило Лопиталя применено два раза. ◄

Замечание

Результат будет таким же и при любом положительном коэффициенте у показателя экспоненты и любом положительном показателе степени х. Этот факт неформально означает, что “экспоненциальная функция растет быстрее, чем степенная при х  + «.

Типовой пример

Найти предел

►Имеет место неопределенность вида . Применим правило Лопиталя.

Здесь правило Лопиталя применено два раза. ◄

Замечание

Результат будет таким же и при любых положительных показателях степеней х и lnx. Этот факт неформально означает, что “степенная функция растет быстрее, чем логарифмическая при х +«.