Результаты вспомогательных вычислений для получения коэффициентов системы нормальных уравнений (4) располагаем в таблице:

I
1 2 3 4 5 6 7	-3 -2 -1 0 1 2 3	12168 13531 18990 22949 22325 23581 24770	4,0852 4,1313 4,2785 4,3608 4,3488 4,3726 4,3939	9 4 1 0 1 4 9	-12,2556 -8,2626 -24,7967 -4,2785 0 4,3488 8,7452 26,2757 13,1817
Сумма	0	-	29,971	28	-24,7969+ 26,2757=1,4790

Подcтавим результаты вычислений в систему (4). Учитывая, что = 7, а, первое уравнение этой системы примет вид, откуда, а тогда.

Второе уравнение системы (4) принимает вид:

, откуда , а тогда.

Следовательно, искомая функциональная зависимость такова:

.

Уравнение показывает, что численность рабочих и служащих в среднем росла ежегодно в 1,129 раза или на 12,9% ежегодно. ◄

4. В случаях, когда между переменными исуществует гиперболическая зависимость

(5)

можно сказать, что между обратными значениями переменной (т.е.) и значениями переменнойсуществует линейная зависимость. Поэтому, если воспользоваться способом наименьших квадратов, то параметрыифункции (5) определяются из следующей системы нормальных уравнений:

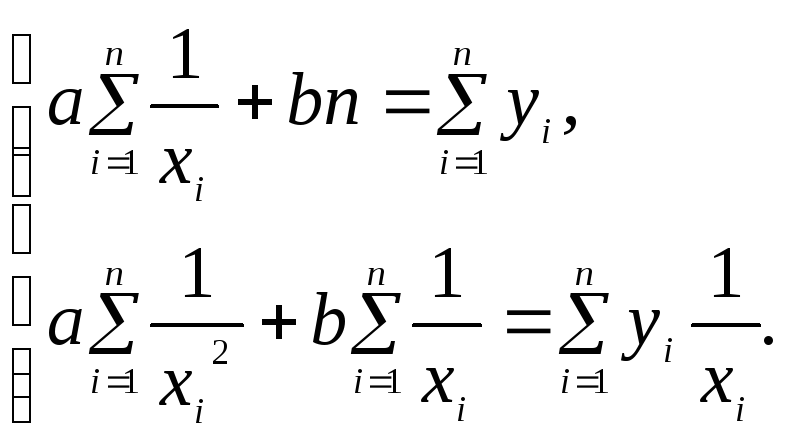, (6)

которая получается из системы (2), если в ней заменить на.

Типовой пример

В таблице приведены данные о стаже рабочего (в годах) и затратах времени на обработку одной детали(мин):

	1	3	5	7	9	11
	34	27	22	18	17	16

Предполагая, что между переменными исуществует гиперболическая зависимость , найти параметры иэтой зависимости, пользуясь способом наименьших квадратов.

►Результаты вспомогательных вычислений поместим в таблице:

				1/xi2
1	1	34	1	1	34
2	3	27	1/3=0,3333	1/9=0,1111	9,0000
3	5	22	1/5=0,2	1/25=0,04	4,4
4	7	18	1/7=0,1429	1/490,0204	2,5714
5	9	17	1/90,1111	1/810,0123	1,8889
6	11	16	1/110,0909	1/1210,0083	1,4545
	-	134	1,8782	1,1921	53,3148

Подставляя полученные значения в систему (6) при = 6 (число пар соответствующих значений переменныхи), получим

,

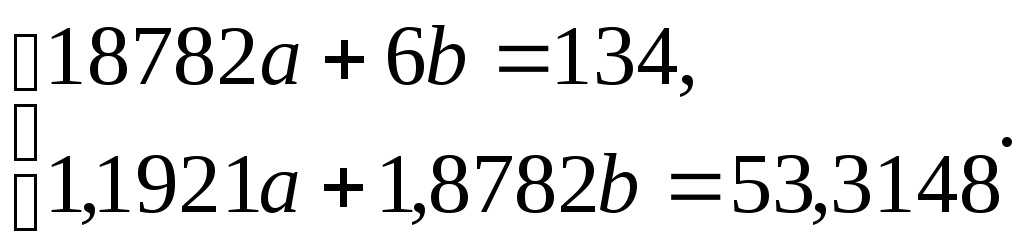Решая эту систему, найдем ,.Следовательно, искомая функциональная зависимость имеет вид:

◄