§9. Метод наименьших квадратов.

В различных практических исследованиях приходится использовать формулы, полученные на основании опыта, наблюдения. Один из лучших способов получения таких формул – метод наименьших квадратов.

Пусть между переменными величинами иимеется или предполагается некоторая функциональная зависимость, подлежащая определению. С этой целью выполнены наблюдения, а результаты их представлены в таблице в видеn пар соответствующих значений переменных и:

			………		………..
			………		………..

Эти данные можно представить графически, если в прямоугольной системе координат построить точки, координаты которых – пары соответствующих значений переменных и, т.е. точки.

Графически это может выглядеть так:

,

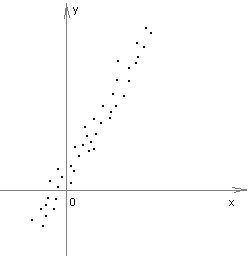или так:

,

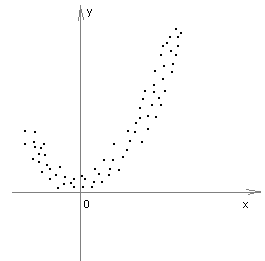а может быть и как-то иначе.

1. Предположим что анализ опытных данных (в том числе и расположение точек на плоскости) привел к выводу, что между переменнымиисуществует линейная зависимость

, (1)

которая графически изображается прямой на плоскости.

Задача сводится к отысканию значений параметров a, b.

Для этого составим функцию - сумма квадратов^*) отклонений предполагаемых значений (аналитических) от фактических.

Исследуем эту функцию на экстремум. А точнее, по понятным причинам, нужно найти точки минимума.

Необходимое условие существования экстремума

,

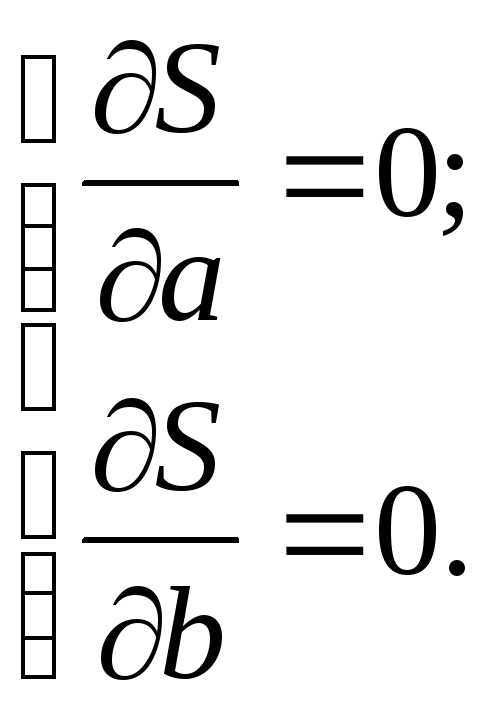т.е.

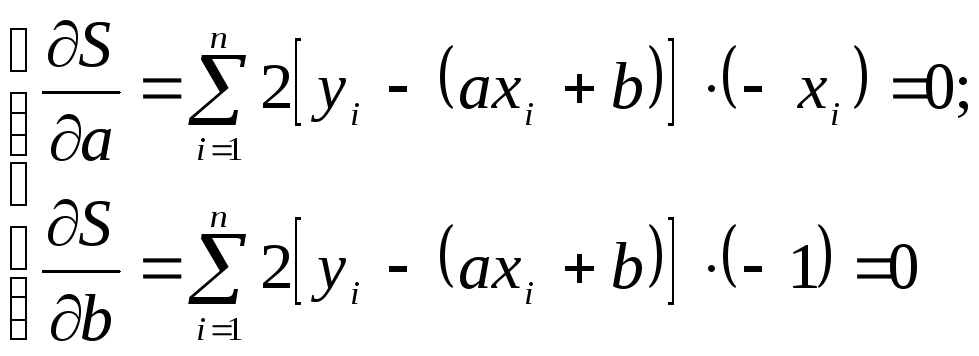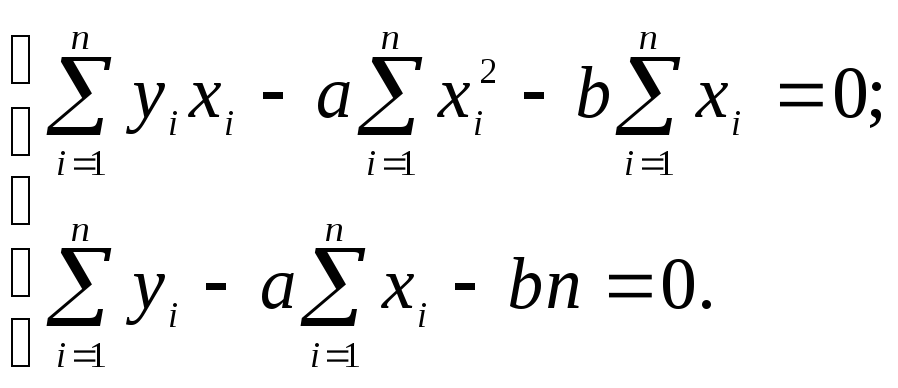или . (2)

Решая эту систему линейных алгебраических уравнений относительно иполучаем их значения, а, следовательно, получаем аналитический вид линейной зависимости исследуемых величин.

Пример

Данные о стоимости основных производственных фондов 5 предприятий (млн. руб.) и среднесуточной переработки свеклы(тыс. ц.) приведены в таблице:

	3	4	5	6	7
	5	5	8	9	11

Предполагая, что между переменными исуществует линейная зависимость, необходимо: а) найти, пользуясь способом наименьших квадратов, параметры этой зависимости; б) определить среднесуточную переработку свеклы предприятием, имеющим стоимость основных фондов 9 млн руб.

►Результаты вспомогательных вычислений для получения коэффициентов системы нормальных уравнений (2) поместим в следующей таблице:

I 2 3 4 5	3 4 5 6 7	5 5 8 9 11	9 16 25 36 49	15 20 40 54 27
	25	38	135	206

Следовательно, система нормальных уравнений при =5 ( число

пар значений переменных) имеет вид:

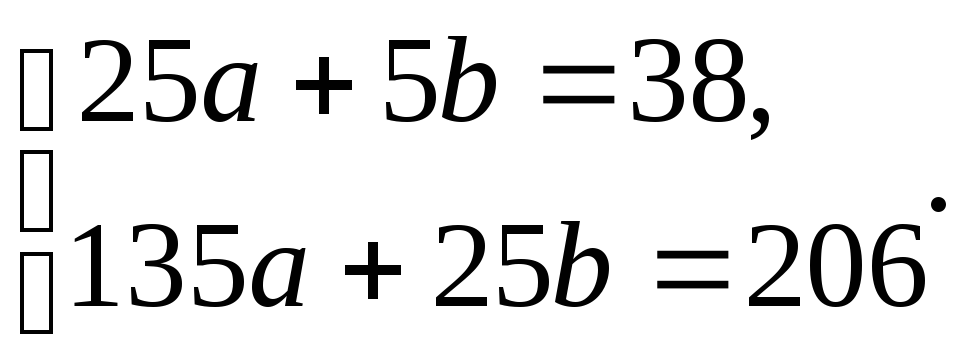
Решая ее, найдем: , а искомая функциональная зависимость такова:.

Среднесуточную переработку свеклы предприятием, имеющим стоимость основных фондов 9 млн. руб. найдем, подставив значение в найденное уравнение зависимости междуи:

(тыс. ц. ) ◄

Типовой пример

Экспериментально получены пять значений искомой функции при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функциюв виде.

.

►Запишем нормальные уравнения для коэффициентов и:

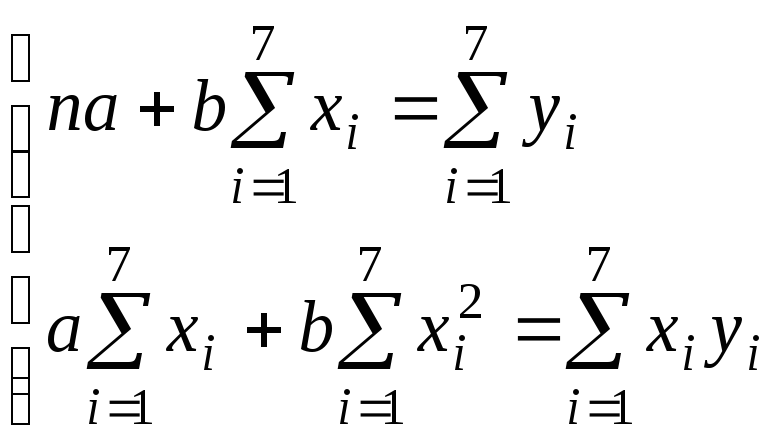
Составим вспомогательную таблицу:

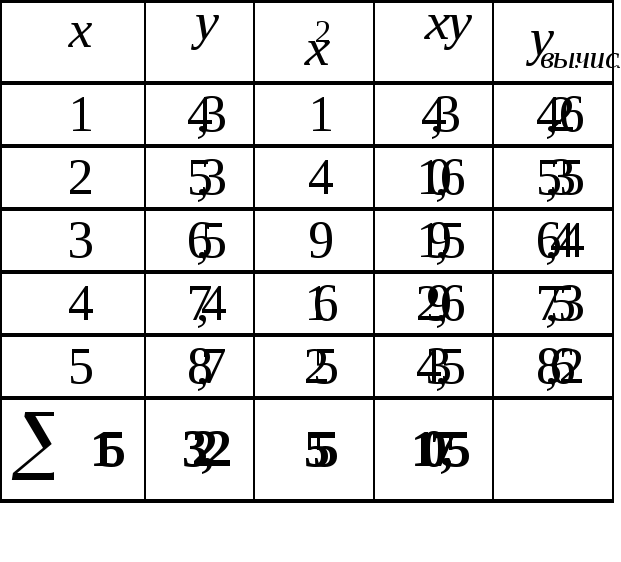
Подставим числовые значения в нормальные уравнения:

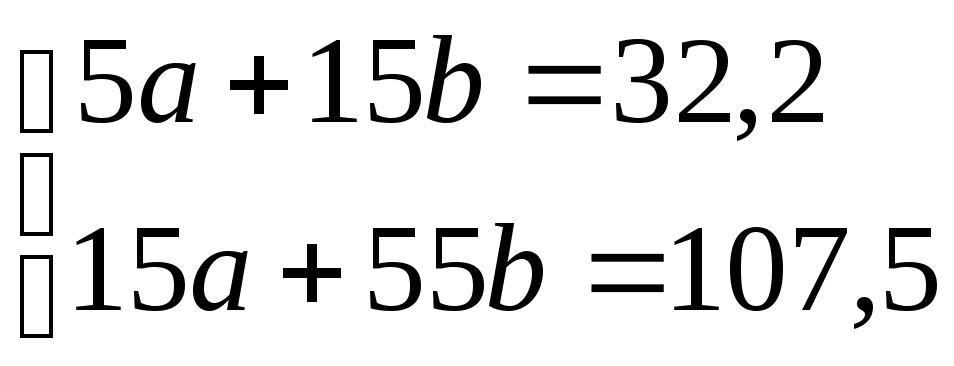. Решив систему, получим ;. Искомая функция имеет вид:. В последнем столбце таблицы запишем значения, вычисленные по полученной формуле.◄

2. Если при нахождении усматривается квадратичная зависимость, то ее следует искать в виде .

Тогда

.

Необходимое условие существования экстремума

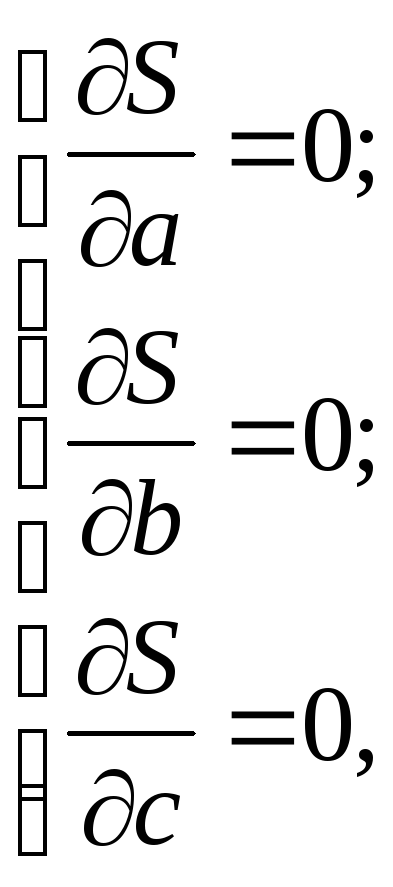т.е. .

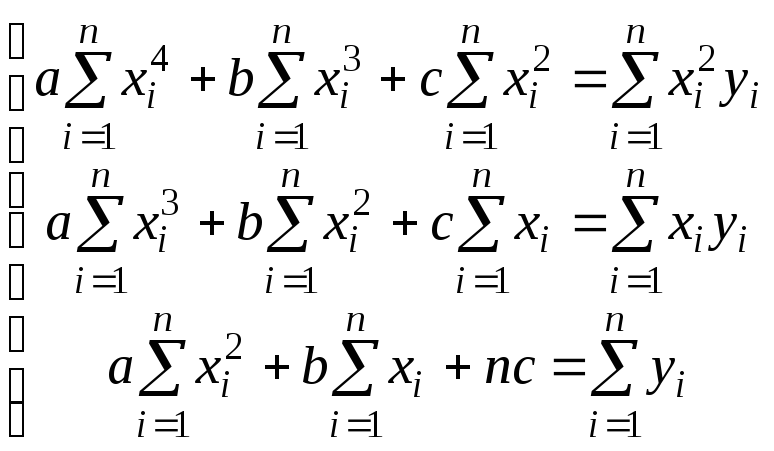Решив эту систему уравнений, получаем значения . А, следовательно, получаем аналитический вид квадратичной зависимостиу от х.

Типовой пример

Результаты наблюдений величины у от х:

х	-2	-1,5	-1	-0,5	1,5	2,5	3	3,5
у	8,8	8,1	4	0,5	-4	-7	-8	-9

Графически:

Определить: а) линейную зависимость у от х;

б) квадратичную зависимость у от х;

в) каково возможное значение у при х=6,3.

а) Линейную зависимость ищем в виде .

Для определения а, b следует составить и решить систему уравнений

.

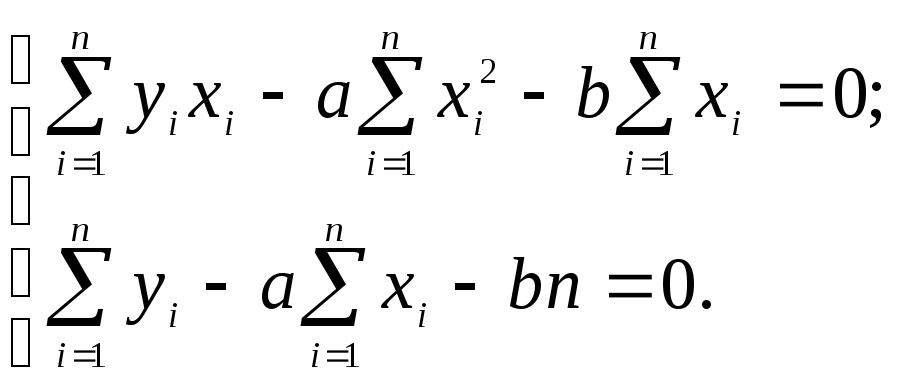Система уравнений имеет вид:

.

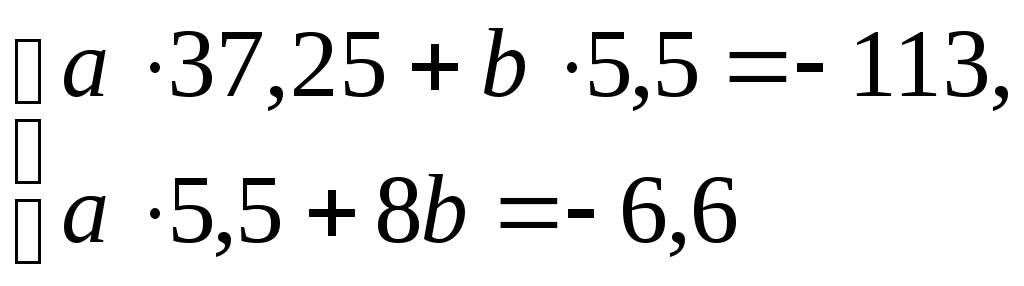Решая ее любым известным способом, получаем a=-3,2, b=0,972.

Значит вид линейной зависимости .

Графически:

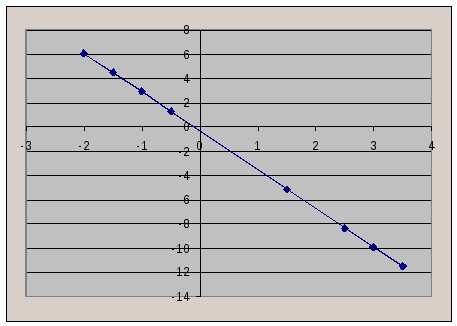
б) Для получения квадратичной зависимости поступаем аналогично. Вид квадратичной зависимости .

Для нахождения коэффициентов a, b, c следует составить систему уравнений

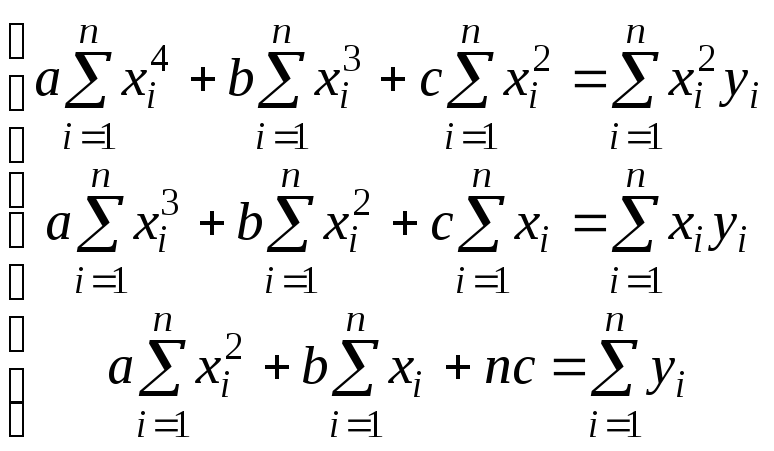
По данным наблюдений получаем систему уравнений:

.

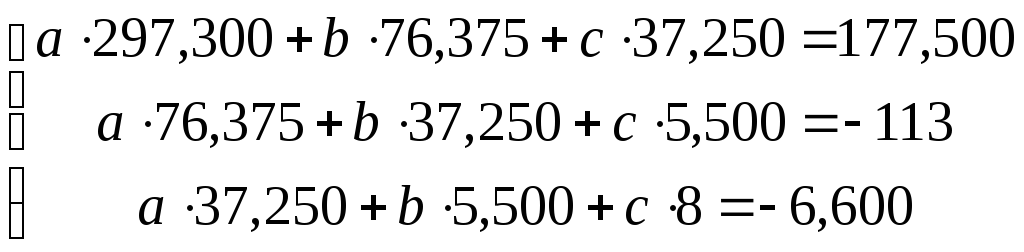Решив эту систему, получаем аналитический вид квадратичной зависимости исследуемого процесса .

Графически:

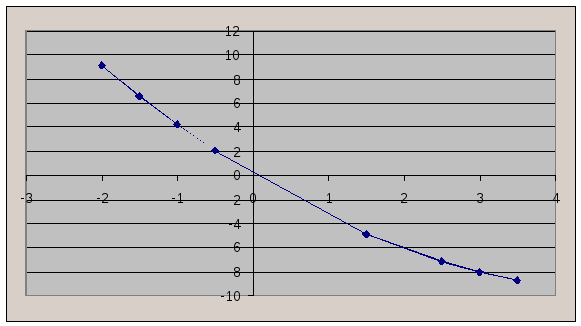
Судите сами, какая из полученных кривых точнее представляет изучаемый процесс.

в) При х=6,3 при линейной зависимости значение у=-20,466; при квадратичной зависимости у=-8,95.

Распространяя действия полученных функций на всю область определения, можно интерполировать, экстраполировать исследуемый процесс.

Существенная разница результатов при экстраполировании в предыдущем примере означает лишь то, что нужны другие критерии (а не на первый взгляд из графика) для выяснения вида функции исследуемого процесса.

3. Пусть зависимость между переменными ивыражается показательной функцией

⁽³⁾

Логарифмируя обе части этого уравнения, получим

.

Следовательно, между значениями переменной и логарифмами

значений переменной существует линейная зависимость с параметрами

и . Поэтому, если воспользоваться способом наименьших

квадратов, то логарифмы ипараметров функции (3) определяются из системы уравнений

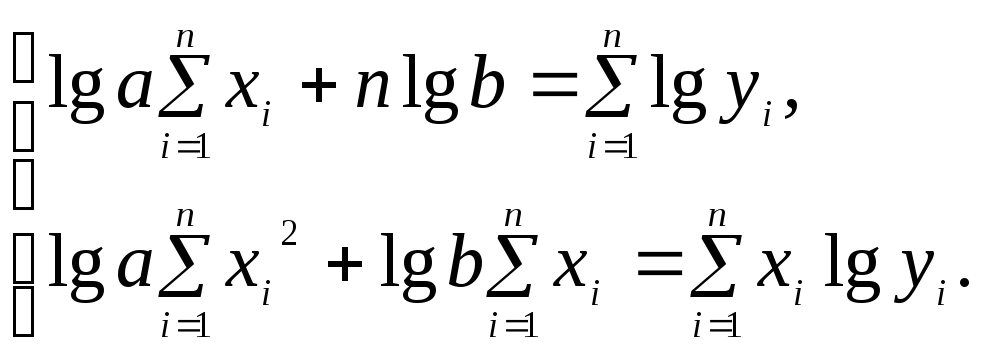, (4)

которая получена из системы (2) заменой в ней иих логарифмами,

а на.

Типовой пример

Средняя годовая численность рабочих и служащих на некотором предприятии характеризуется следующими условными данными:

Годы	1992	1993	1994	1995	1996	1997	1998
Числ - ть раб-х и служащих	12 168	13 531	18 990	22 249	22 325	23 581	24 770

Предполагая, что рост численности рабочих и служащих происходил по показательной кривой , найти параметрыиэтой зависимости, пользуясь способом наименьших квадратов.

►Систему координат выберем так, чтобы 1995г. соответствовало ее начало - это упростит вычисления. Следовательно, при решении задачи исходим из следующих данных:

Годы	-3	-2	-1	0	1	2	3
Численность рабочих и служащих	12 168	13 531	18 990	22 949	22 325	23 581	24 770