2.Условный экстремум функции двух переменных

Пример

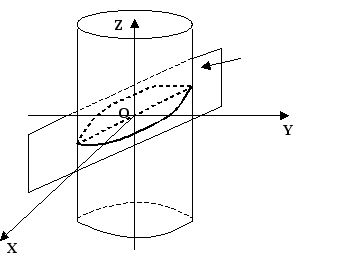
Найти экстремум функции при условии, чтох и у связаны соотношением: . Геометрически задача означает следующее: на эллипсе, полученном при пересечении цилиндраплоскостью, требуется найти максимальное или минимальное значение аппликаты.

Эту задачу можно решать так: из уравнения находим. Подставляя найденное значение у в уравнение плоскости, получаем функцию одной переменнойх:

Тем самым задача о нахождении экстремума функции при условии, что, свелась к задаче нахождения экстремума функции одной переменной, на отрезке.

Геометрически задача означает следующее: на эллипсе , полученном при пересечении цилиндраплоскостью, требуется найти максимальное или минимальное значение аппликаты(рис.9). Эту задачу можно решать так: из уравнениянаходим. Подставляя найденное значение у в уравнение плоскости, получаем функцию одной переменнойх:

Тем самым задача о нахождении экстремума функции при условии, что, свелась к задаче нахождения экстремума функции одной переменной, на отрезке.

Итак, задача отыскания условного экстремума – это задача о нахождении экстремума целевой функции , при условии, что переменныех и у подчиняются ограничению , называемомууравнением связи.

Будем говорить, что точка , удовлетворяющая уравнению связи,является точкой локального условного максимума (минимума), если существует окрестность такая, что для любых точек, координаты которых удовлетворяют уравнению связи, выполнено неравенство.

Если из уравнения связи можно найти выражение для у, то, подставляя это выражение в исходную функцию, превращаем последнюю в сложную функцию одной переменной х.

Общим методом решения задачи на условный экстремум является метод множителей Лагранжа. Составим вспомогательную функцию, где─ некоторое число. Это функция называетсяфункцией Лагранжа, а ─ множителем Лагранжа. Таким образом, задача нахождения условного экстремума свелась к нахождению точек локального экстремума для функции Лагранжа. Для нахождения точек возможного экстремума надо решить систему из 3-х уравнений с тремя неизвестнымих, у и.

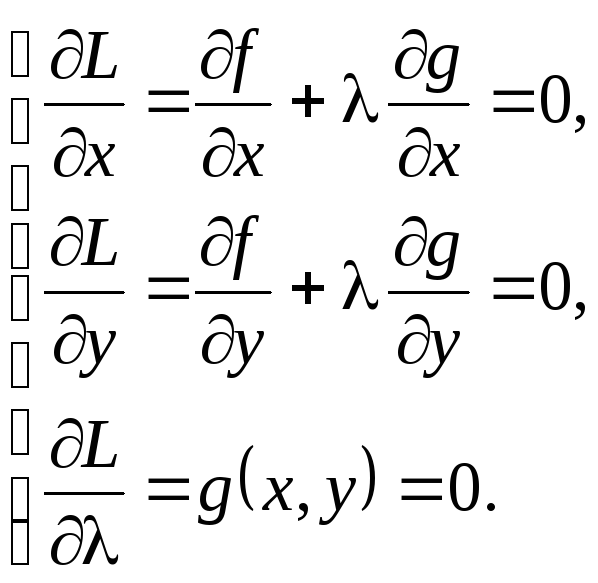
Затем следует воспользоваться следующим достаточным условием экстремума.

ТЕОРЕМА. Пусть точка является точкой возможного экстремума для функции Лагранжа. Предположим, что в окрестности точкисуществуют непрерывные частные производные второго порядка функцийи. Обозначим

Тогда, если , то─ точка условного экстремума функциипри уравнении связипри этом, если, то─ точка условного минимума, если, то─ точка условного максимума.

§8. Градиент и производная по направлению

Пусть функция определена в некоторой (открытой) области. Рассмотрим любую точкуэтой области и любую направленную прямую (ось), проходящую через эту точку (рис. 1). Пусть– какая-нибудь другая точка этой оси,­– длина отрезка междуи, взятая со знаком «плюс», если направлениесовпадает с направлением оси, и со знаком «минус», если их направления противоположны.

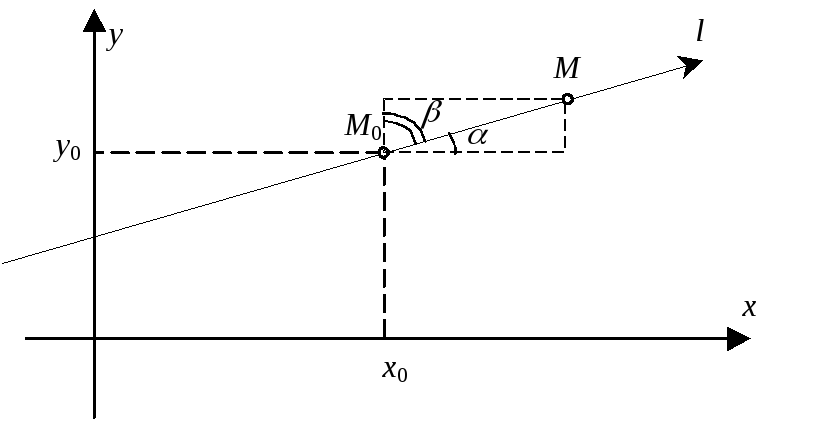
Рис. 1

Пусть неограниченно приближается к. Предел

называется производной от функции по направлению (или вдоль оси) и обозначается следующим образом:

.

Эта производная характеризует «скорость изменения» функции в точке по направлению. В частности, и обычные частные производные,также можно рассматривать как производные «по направлению».

Предположим теперь, что функция имеет в рассматриваемой области непрерывные частные производные. Пусть осьобразует с осями координат углыи. При сделанных предположениях производная по направлениюсуществует и выражается формулой

.

Если вектор задан своими координатами, то производную функциипо направлению вектораможно вычислить по формуле:

.

Вектор с координатами называетсявектором-градиентом функции в точке. Вектор-градиент указывает направление наиболее быстрого возрастания функции в данной точке.

Пример

Дана функция , точка A(1, 1) и вектор . Найти: 1)grad z в точке A; 2) производную в точке A по направлению вектора .

►Частные производные данной функции в точке :

; .

Тогда вектор-градиент функции в этой точке: . Вектор-градиент еще можно записать с помощью разложения по векторами:

. Производная функции по направлению вектора:

. Итак, ,.◄