§7.Наибольшее и наименьшее значения функции многих переменных в замкнутой области

1.Точкой глобального максимума (минимума) функции на множественазывается точка , в которой функция достигает своего наибольшего или наименьшего значения ТЕОРЕМА. Пусть в ограниченной и замкнутой области задана дифференцируемая функция . Тогда эта функция достигает в области D своего наибольшего и наименьшего значения (так называемый глобальный экстремум). Эти значения могут достигаться либо в критических точках внутри области, либо на ее границе. Поэтому внутри области нужно найти все точки, в которых возможен экстремум. Затем, не выясняя, имеет ли функцияв этих точках экстремум, вычислить значения функции во всех найденных точках. Однако функция может принимать наибольшее и наименьшее значения и на границе области. Поэтому нужно отдельно найти наибольшее и наименьшее значения функции на границе области. При этом надо использовать уравнения границы, что позволяет уменьшить число независимых переменных у функции и свести задачу к исследованию функции одной переменной. Сравнивая все полученные таким образом значения функции, выбираем из них наибольшее и наименьшее.

Типовой пример

Найти наибольшее и наименьшее значения функции в замкнутой области (D), заданной неравенствами , , .

►И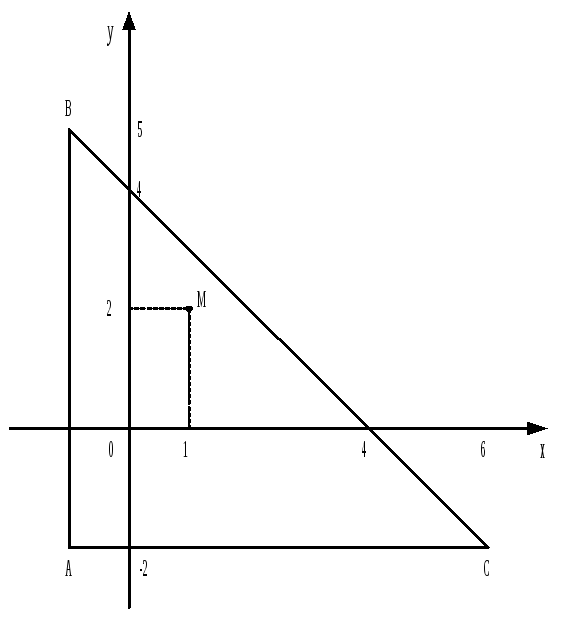зобразим область (D); она представляет собой треугольник с вершинами A|(-1; -2), B(-1; 5), C(6; -2). Найдём стационарные точки. , . Решим систему уравнений

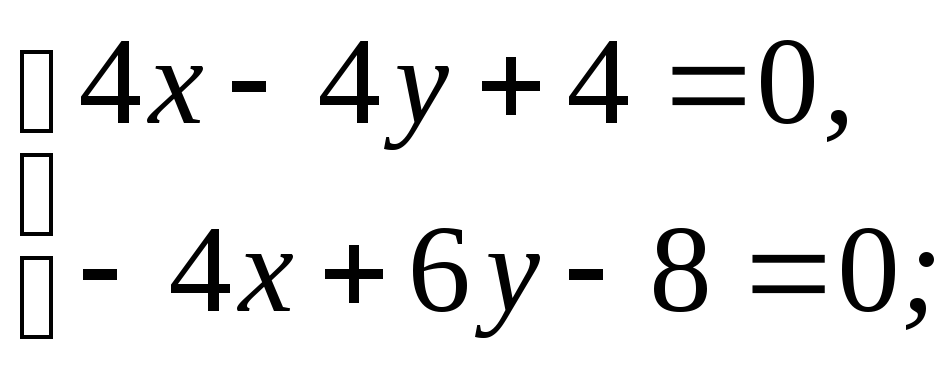
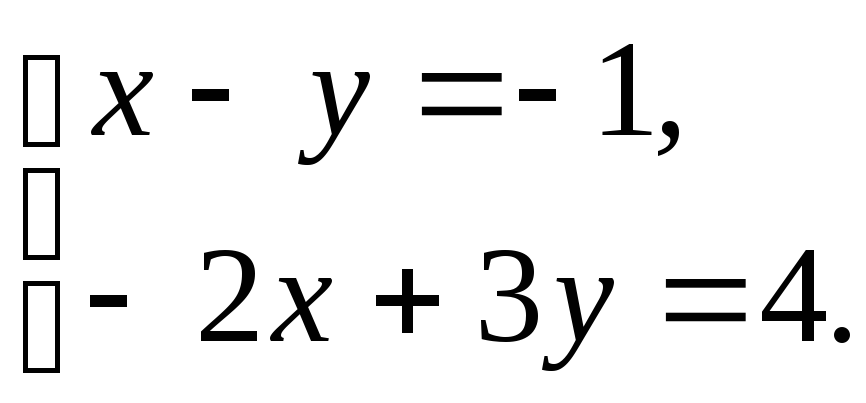
Решением этой системы является x=1, y=2. Стационарная точка M(1;2) принадлежит области (D), так как её координаты удовлетворяют всем трём неравенствам, задающим треугольник (D). Найдём значение функции в этой точке: u(M) = 2 – 8 + 12 + 4 – 16 + 5 = –1.

Исследуем функцию на границе области (D). Граница представляет собой объединение трёх отрезков:– отрезкаBC, – отрезкаAB, – отрезкаAC.

1) . = 2x² – 4x(4 – x) +

+ 3(4 – x)² + 4x – 8(4–x) + 5 = 2x² – 16x + 4x² + 3(16 – 8x + x²) + 4x –

– 32 + 8x + 5 = 9x² – 28x + 21. Найдём наибольшее и наименьшее значения функции 9x² – 28x + 21 на отрезке [–1; 6]. Имеем 18x – 28; x = 14/9 – стационарная точка функции , 14/9  [–1; 6]. Обозначим N₁(14/9 ; 4 –14/9 ) или N₁(14/9 ; 22/9 ). u(N₁) = ==196/9 – 392/9 + 21 = –34/9. Найдём значенияна концах отрезка [–1; 6]:=u(B) = 58; =u(C) = 177. Наибольшим из этих значений является u(C) = 177, наименьшим – u(N₁) = – 34/9.

2). = 2 + 4y + 3y² – 4 – 8y +

+5 = 3y² – 4y + 3. Найдём наибольшее и наименьшее значения функции = 3y² – 4y + 3 на отрезке [–2; 5]; = 6y – 4; y = 2/3 – стационарная точка функции , принадлежащая отрезку [–2; 5]. ОбозначимN₂(–1; 2/3). U(N₂) = . Найдём значения функциина концах отрезка [– 2; 5]:=u(A) = 23; =u(B) = 58.

3) . = 2x² + 8x + 12 + 4x + + 16 + 5 = 2x² + 12x + 33. Обозначим = 2x² + 12x + 33.

= 4x + 12. Стационарная точка x = – 3 не принадлежит отрезку

[–1; 6], поэтому она нас не интересует. Значения на концах отрезка

[–1; 6] были найдены ранее: =u(A) = 23, =u(C) = = 177.

Сравнивая все полученные значения, находим =u(C) = = u(6; –2) = 177, = u(M) = u(1; 2) = – 1. ◄

Типовой пример

Найти наибольшее и наименьшее значения функции в области, заданной неравенствами:,.

►1. Изобразим область:

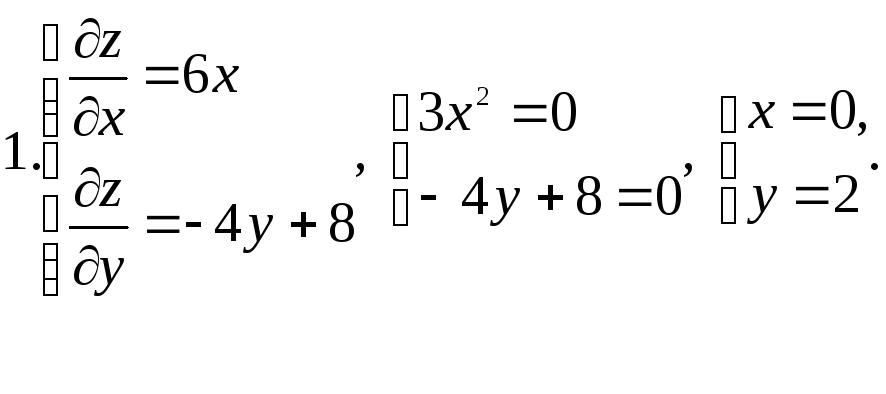
2. Точка не принадлежит области.

3. Граница областисостоит из трех гладких частейгдеизаданы уравнениями:.

3.1. На части границы, следовательно на, где. Теперь встала задача нахождения наибольшего и наименьшего значения функции одной переменнойна промежутке. Так как, то точкаявляется стационарной точкой функции, и эта точка при­надлежит промежутку. Этому значению переменнойнасоответст­вует значение. Соответствующая точка -.

3.2. На части границы, следовательно, на, где. Исследуем функциюна промежутке. Так как, то точкаявляется стационарной точкой функции, но эта точка не принадлежит промежутку.

3.3. На части границы, следовательно на, где. Исследуем функциюна промежутке. Так как, то точкаявляется стационарной точкой функции,и эта точка принадлежит промежутку. Соответствующая точка.

4. Таким образом, имеется всего пять точек, в которых нужно вычис­лить значения функции :;;;;. В результате вычислений получаем:;;;;. Следовательно,,. ◄