§4. Дифференцирование сложных функций

1. Случай одной независимой переменной

Пусть есть дифференцируемая функция двух переменныхипричем аргументы этой функции сами являются дифференцируемыми функциями независимой переменной:иТогда сложная функциядифференцируема, и ее производнаявычисляется по формуле

.

Пусть теперь гдеТогдат. е. функцияесть функция одной переменнойЭтот случай сводится к предыдущему, где роль переменнойиграет“Полная” производная функциипоравна

.

Типовой пример

Найти , еслигде

►Имеем

◄

Типовой пример

Найти частную производную и полную производнуюеслиа.

►Имеем

◄

2. Случай нескольких независимых переменных

Предположим теперь, что гдеиТогдаесть сложная функция двух независимых переменныхиЧастные производные этой сложной функции находят по формулам

и .

Эти формулы обобщаются на случай сложной функции любого конечного числа аргументов. Во всех случаях справедлива формула

(свойство инвариантности формы полного дифференциала).

Пример

Найти частные производные иесли,

►Имеем

, , ;

◄

§5. Неявные функции и их дифференцирование

Пусть - дифференцируемая функция трех переменныхии пусть уравнениеопределяеткак функцию независимых переменныхиЧастные производные этой неявной функциив точкевычисляются по следующим формулам:

и

при условии, что гдеи

Типовой пример

Найти частные производные иеслиопределяется, как функция отииз уравнения

.

►Обозначим левую часть данного уравнения через Тогда

,

,

.

Отсюда получаем

; .◄

§6.Экстремум функции многих переменных

Пусть функция определена в некоторой окрестности точки. Говорят, что точкаявляетсяточкой максимума (минимума) функции , если существует окрестностьточки, такая что для любой точкииз этой окрестности, отличной от точки, справедливо неравенство. Точки максимума и точки минимума функции называютточками экстремума функции, а значения функции в этих точках – экстремумами функции.

ТЕОРЕМА (необходимое условие экстремума). Если – точка экстремума дифференцируемой функции, то

. . . . (1)

Точка , в которой выполнены условия (1), называетсястационарной точкой. Не любая стационарная точка функции является точкой экстремума. Нижеследующая теорема достаточное условие для того, чтобы стационарная точка функции двух переменных была точкой экстремума.

ТЕОРЕМА (достаточное условие экстремума для функции двух переменных). Пусть – стационарная точка функции двух переменных, дважды непрерывно дифференцируемой в некоторой окрестности точки М. Рассмотрим определитель

.

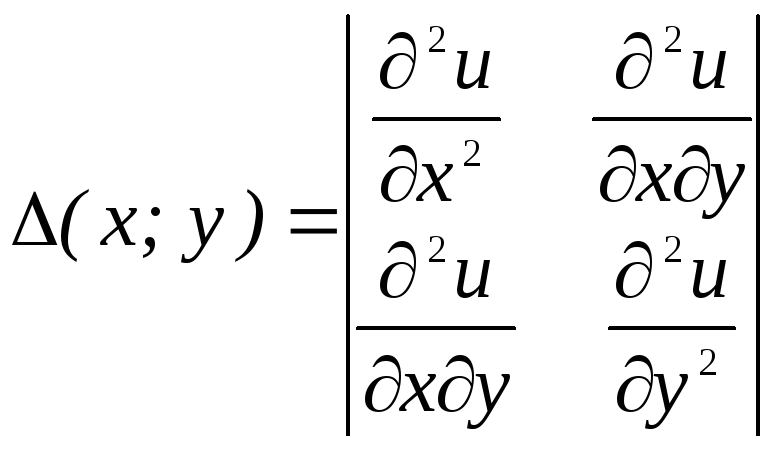1. Если , тоявляется точкой экстремума функции, а именно: а) если, то– точка минимума; б) если, то– точка максимума.

2. Если , тоне является точкой экстремума.

3. Если , то нужны дополнительные исследования (экстремум может быть, а может отсутствовать)

Типовой пример

Найти точки экстремума функции

.

►Найдём стационарные точки функции ,. Решим систему уравнений

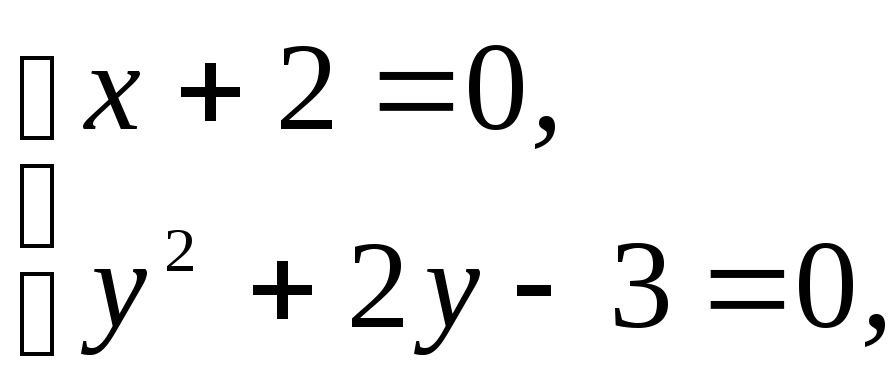
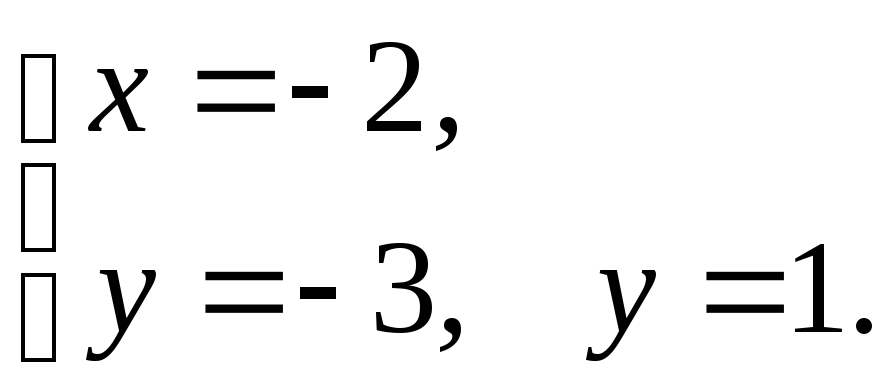
Решением системы являются точки . Исследуем эти стационарные точки на экстремум, для чего найдём частные производные второго порядка:

, ,.

Имеем

.

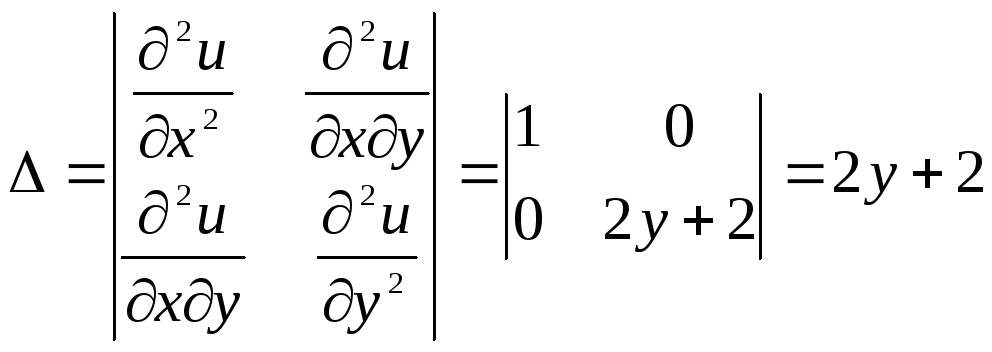, следовательно, не является точкой экстремума. , что говорит о том, что является точкой экстремума. А так как, то заключаем, что– точка минимума. ◄

Приведём примеры, иллюстрирующие пункт 3.

1. ─ точка возможного экстремума;, следовательно, в точке,

однако в этой точке функция имеет минимум, т.к. нодля всех точек из области определения.

2.─ точка возможного экстремума;следовательно, в точке, однако в точкев этом случае экстремума нет. Так как, а. Значитприипри. Получили, что в любой окрестности точкифункция принимает значения разных знаков.