4. Непрерывность по отдельным переменным

Зафиксируем переменную , полагая, а переменнойпридадим произвольное приращение. Функцияполучит приращение

,

которое называется частным приращением функции в точке , соответствующим приращению аргумента. Заметим, чтоявляется функцией одной переменной. Аналогично,

.

Функция называетсянепрерывной в точке по переменной (по переменной ), если

().

В отличие от непрерывности по отдельным переменным обычную непрерывность функции называют иногда непрерывностью по совокупности переменных.

ТЕОРЕМА 3. Если функция определена в некоторой окрестности точки и непрерывна в этой точке, то она непрерывна в этой точке по каждой из переменных.

Обратное утверждение неверно.

Типовой пример

Докажем, что функция

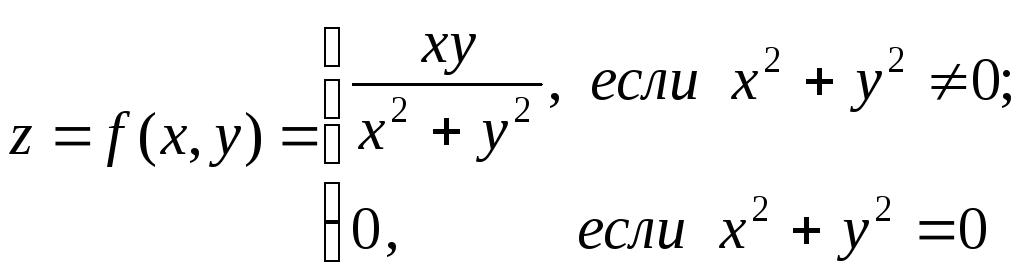
непрерывна в точке по каждой переменнойи, но не является непрерывной в этой точке по совокупности переменных.

►Рассмотрим частное приращение функции в точке, соответствующее приращениюаргумента:

.

Очевидно, что , а это означает, чтонепрерывна в точкепо переменной.

Аналогично можно доказать непрерывность в точкепо переменной.

Покажем, что предел 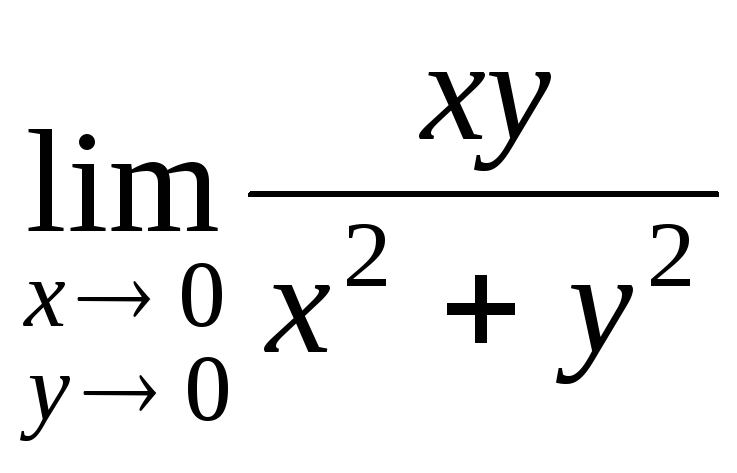не существует. Пусть точкастремиться к точкепо прямой, проходящей через точку. Тогда получим

.

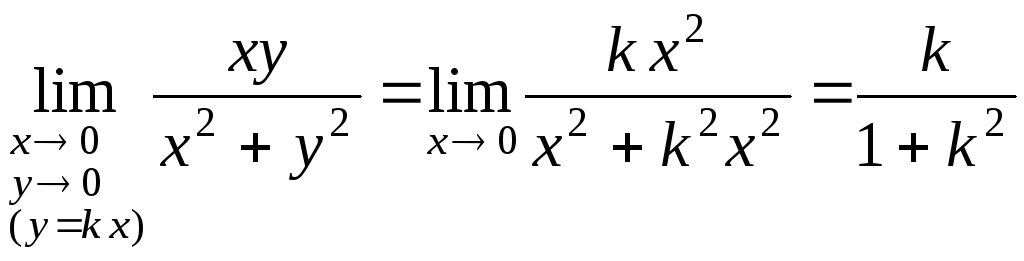Таким образом, приближаясь к точке по различным прямым,соответствующим разным значениям , получаем разные предельные значения. Отсюда следует, что предел данной функции в точкене существует, а значит, функцияне является непрерывной в этой точке. ◄

§2. Частные производные

1. Частные производные первого порядка

Рассмотрим функцию двух переменных Придавая значению переменнойприращениерассмотрим предел (при)

Этот предел называется частной производной (первого порядка) данной функции по переменной в точкеи обозначаетсяилиТочно так же определяется частная производная этой функции по переменнойи обозначаетсяили

Частные производные вычисляются по обычным формулам дифференцирования, при этом все переменные, кроме одной рассматриваются как постоянные.

Типовой пример

Найти частные производные функции

►Считая величину постоянной, получаем

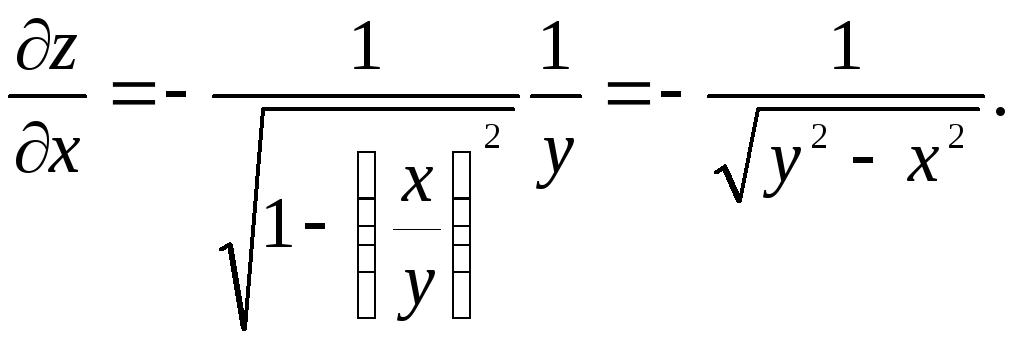
Считая величину постоянной, получаем

◄

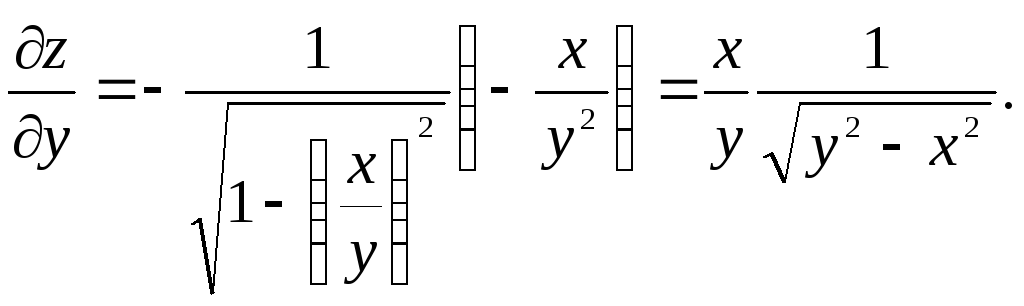2. Частные производные высших порядков

Пусть есть функция двух переменныхиЧастными производными второго порядка функции называются частные производные от ее частных производных первого порядка, если они существуют.

Частные производные второго порядка обозначаются следующим образом:

Аналогично определяются и обозначаются частные производные более высокого порядка. Частная производная второго или более высокого порядка, взятая по нескольким различным переменным, называется смешанной частной производной. Относительно смешанных частных производных имеет место следующая ТЕОРЕМА.

ТЕОРЕМА. Две смешанные частные производные одной и той же функции, отличающиеся лишь порядком дифференцирования, равны между собой при условии их непрерывности.

Типовой пример

Найти частную производную от функции

►Имеем

◄

§3. Полный дифференциал и его применение

Пусть дана функция двух переменных Предположим, что ее аргументыиполучают соответственно приращенияиТогда функцияполучаетполное приращение

Геометрически полное приращение равно приращению аппликаты графика функциипри переходе от точкив точку

Функция называется дифференцируемой в точкеесли ее полное приращениеможет быть представлено в виде

где а- бесконечно малая более высокого порядка, чемЕсли функциядифференцируема в данной точке, то ееполным дифференциалом называется главная часть полного приращения этой функции, линейная относительно ит. е.

Дифференциалы независимых переменных, по определению, равны их приращениям Для дифференциала функциисправедлива формула

Заменяя приближенно приращение функции ее дифференциалом (в предположении достаточной малости значений иполучим

Отсюда имеем

Все изложенное распространяется на функции трех и более переменных.

Типовой пример

Вычислить приближенно

►Искомое число будем рассматривать как значение функции приеслиПрименяя формулу

получаем

Следовательно,

◄