II. Вопросы промежуточного контроля

1. Что называется функцией двух переменных, ее областью оп­ределения? Дайте геометрическое толкование этих понятий.

2. Что называется функцией трех переменных, ее областью определений? Как можно геометрически истолковать область опреде­ления функции трех переменных?

3. Что называется поверхностью уровня и линией уровня?

4. Что называется пределом функции двух переменных в точке? В каком случае эта функция называется непрерывной в точке, в области?

5. Что называется точкой разрыва функции двух переменных?

6. Как определяются частные производные? Сформулируйте пра­вила нахождения частных производных функций нескольких пере­менных. Выясните геометрический смысл частных производных функ­ции двух переменных.

7. Когда функция 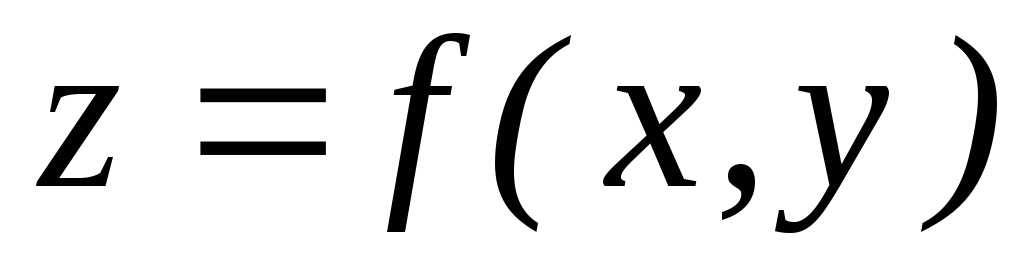называется дифференцируемой в данной точке? Что называется полным дифференциалом этой функ­ции в данной точке

8. Выведите уравнения касательной плоскости и нормали к по­верхности в точке М_о. Выясните геометрический смысл полного дифференциала функции двух переменных

9. . Выведите формулу дифференцирования неявной функции 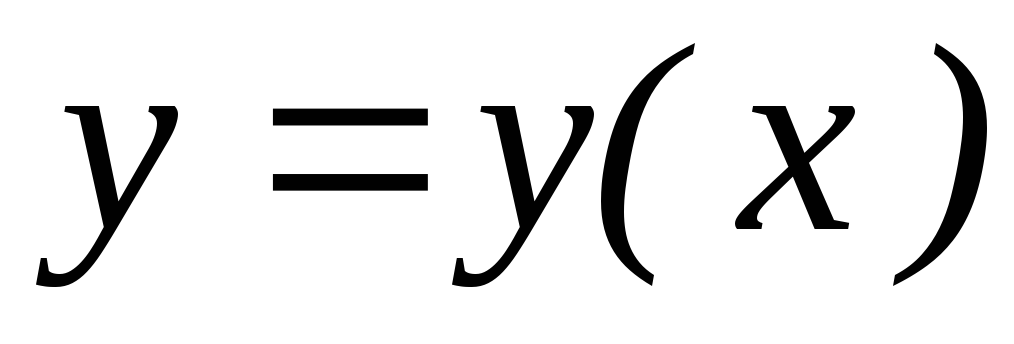,заданной уравнением F(x, y)=0.

10. Дайте определение частных производных высших порядков. Сформулируйте теорему о равенстве смешанных частных производ­ных функции двух переменных.

11. Что называется производной от функции" и=и(х, у, z) в данной точке Мо по направлению вектора s? Выведите формулу для ее вычисления.

12. Что называется градиентом скалярного поля и=и(х, у, z) в данной точке? Как выражается производная по направлению че­рез градиент и единичный вектор? Сформулируйте известные вам свойства градиента.

13. Что называется максимумом (минимумом) функции двух переменных? Выведите необходимые условия и сформулируйте до­статочные условия экстремума функции двух переменных.

14. Сформулируйте правило нахождения экстремумов функции двух переменных.

15. Выведите правило нахождения наибольшего и наименьше­го значений функции двух переменных в замкнутой области.

16. Что называется условным экстремумом функции z=f(x, г/)? Изложите метод нахождения условных экстремумов функция двух переменных, если эти переменные связаны одним условием.

17. В чем состоит метод наименьших квадратов при нахождении функции на основании экспериментальных данных?

*⁾Иначе слагаемые могут взаимно уничтожиться: отклонения могут быть как с “+”, так и с “–“.