Глава 1. Дифференциальное исчисление

ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

§1. Понятие функции нескольких переменных

1. Произвольный упорядоченный набор из действительных чиселобозначаетсяи называется точкой-мерного арифметического пространства сами числа называются координатами точки

Пусть - произвольное множество точек-мерного арифметического пространства. Если каждой точкепоставлено в соответствие некоторое действительное числото говорят, что на множествезадана числовая функция отпеременныхМножествоназывается областью определения функции

Рассмотрим частный случай, когда .Пусть дано множество , и пусть указано правило, по которому каждой точкесоответствует некоторое число. В этом случае говорят, чтозадана функция с областью определенияи областью значений. При этоминазываютнезависимыми переменными (аргументами), а –зависимой переменной (функцией).

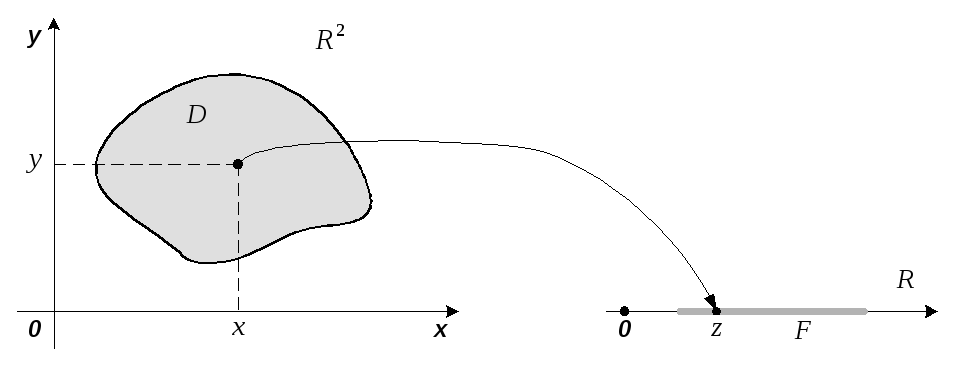Функциючасто записывают в виде «». Схематично функция может быть изображена так, как это показано на рисунке.

П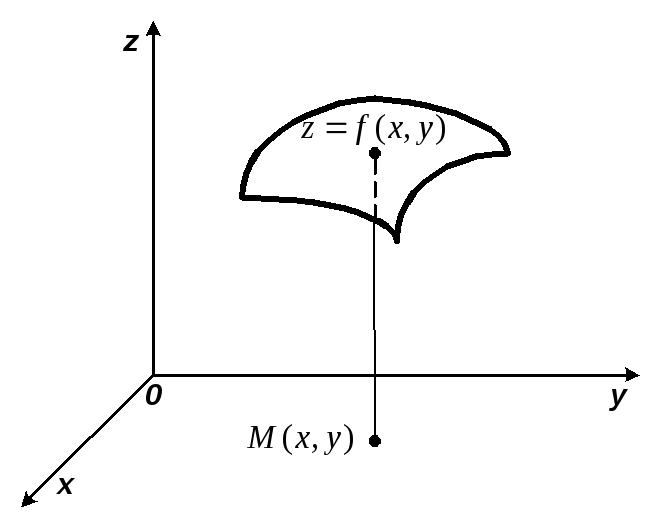ример

На множестве определим функцию; тогда ее областью значений является отрезок. Эту функцию можно определить, конечно, и на всей плоскости; в этом случае имееми.

Частное значение функции приобычно записывают в виде

или.

Типовой пример

Найти область определения функции . Найти .

►Областью определения функции является решение неравенства или . Последнее неравенство определяет круг радиуса 2 с центром в точке 0(0; 0). .◄

Графиком этой функции называется множество точек пространства

представляющее собой некоторую поверхность в

При построении графика функции часто пользуются методом сечений.

Пример

Построить график функции и найти.

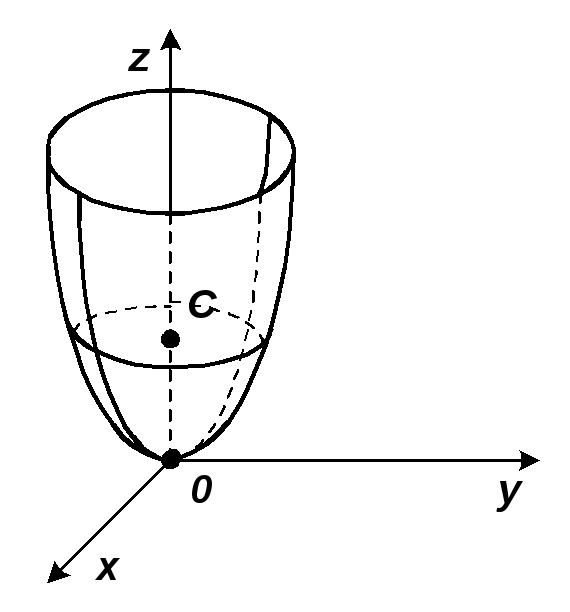►Воспользуемся методом сечений.

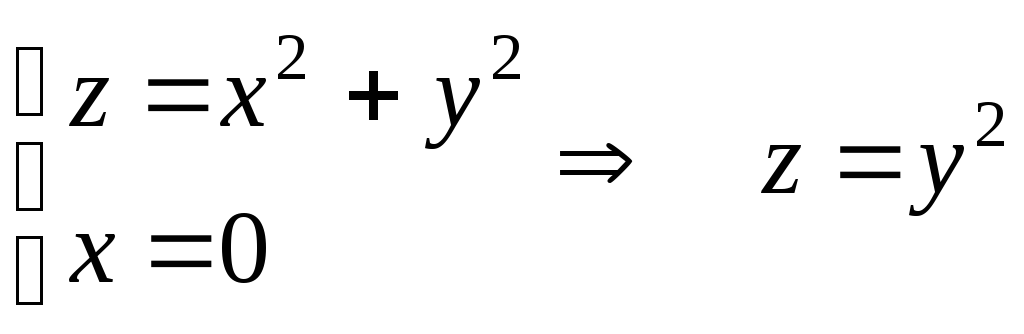–в плоскости – парабола.

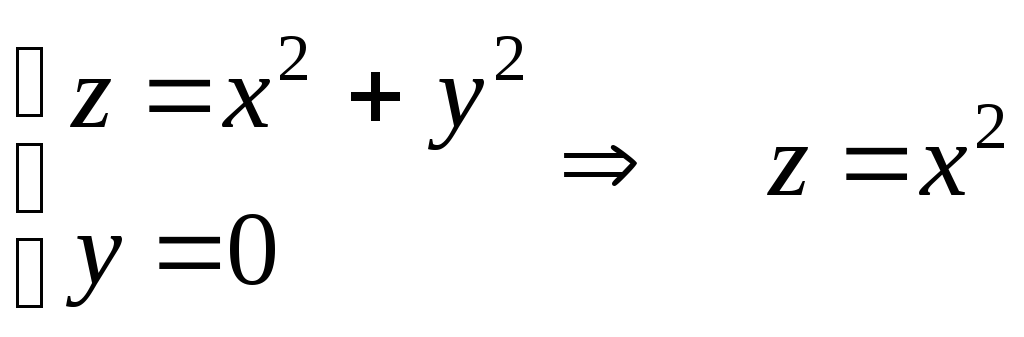–в плоскости –парабола.

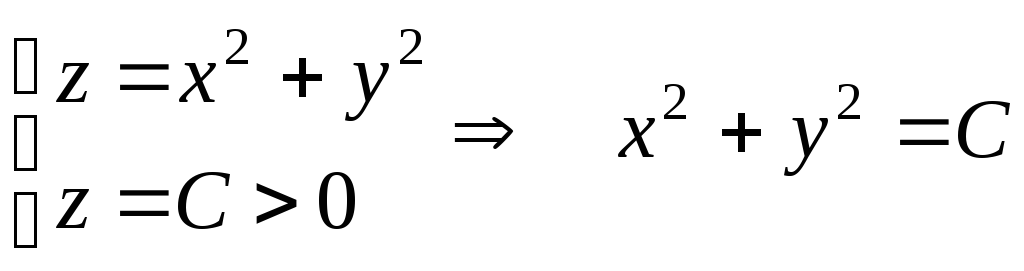–в плоскости – окружность.

Искомая поверхность – параболоид вращения.◄

В некоторых случаях наглядное представление о функции двух или трёх переменных может дать картина её линий уровня.

Линией уровня функции называется множество точек МплоскостиОху, удовлетворяющих равенству, гдес – константа.

Другими словами, линия уровня есть кривая, во всех точках которой функция принимает одно и то же постоянное значениес. Геометрически линии уровня получаются как проекции на плоскость Oxy линии пересечения графика функции и горизонтальной плоскости .

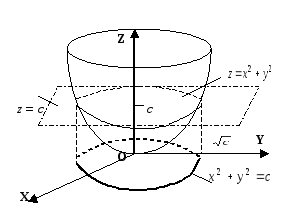
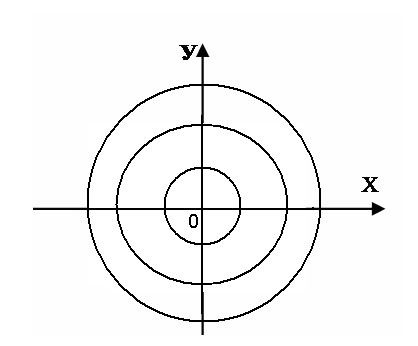
Рис. 2

Пример

Линиями уровня функции являются окружности, то есть линии пересечения поверхностис плоскостями(рис. 2).

Линии уровня используются в картографии. Так, например, на топографических картах рисуют линии равной высоты над уровнем моря, на метеорологических картах изображают линии одинакового давления – изобары.

По линиям уровня, построенным для некоторой рассматриваемой функции с одинаковыми промежутками между значениями , можно получить представление о графике функции (то есть о форме поверхности). В тех местах, где линии располагаются «гуще», функция при переходе от одного значенияс к другому меняется быстрее, чем там, где линии распределены реже.

Расстоянием между двумя произвольными точками и(евклидова) пространстваназывается число

.

Множество точекназываетсяоткрытым кругом радиуса с центром в точке,–окружностью радиуса с центром в точке.

Открытый круг радиуса с центром в точкеназывается -окрестностью точки .

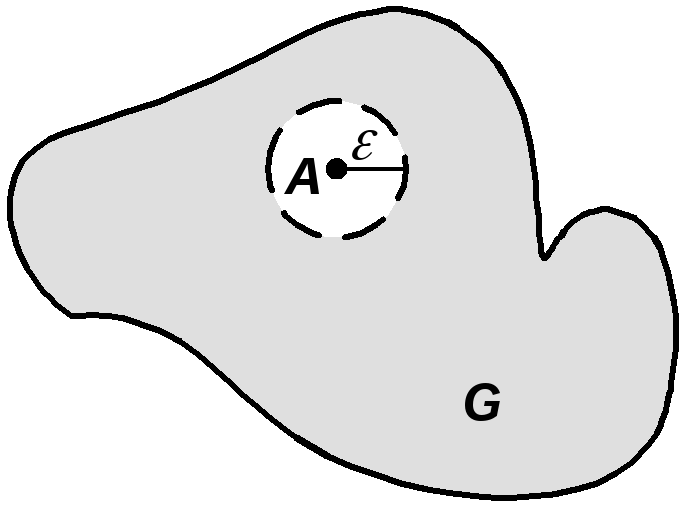Определение. Точканазываетсявнутренней точкой множества , если существует-окрестностьточки, целиком принадлежащая множеству(т.е.)

Точка называетсяграничной точкой множества , если в любой ее-окрестности содержатся точки, как принадлежащие множеству, так и не принадлежащие ему. Граничная точка множества может как принадлежать этому множеству, так и не принадлежать ему.

Множество называетсяоткрытым, если все его точки – внутренние.

Множество называетсязамкнутым, если оно содержит все свои граничные точки. Множество всех граничных точек множества называется егограницей (и часто обозначается символом ). Заметим, что множествоявляется замкнутым и называетсязамыканием множества .

Пример

Если , то. При этом.

Точка называетсяпредельной точкой множества , если в любой-окрестности точкисодержатся точки множества, отличные от.

Образно говоря, точка называется предельной точкой множества , если «к точкеможно подойти сколь угодно близко, идя по точкам множестваи не наступая на саму точку». Предельная точка множества может принадлежать, а может не принадлежать этому множеству.

Пример

Множество совпадает с множеством своих предельных точек. Множествоимеет единственную предельную точку.