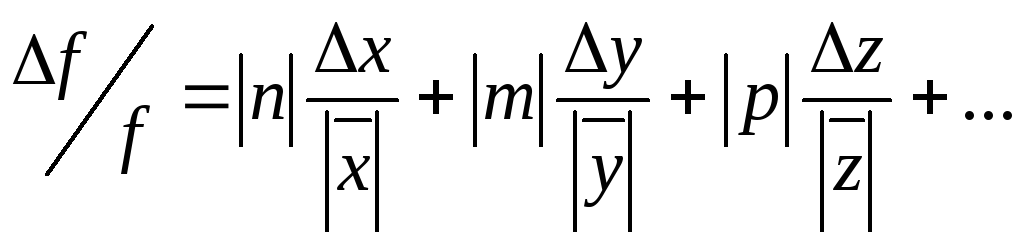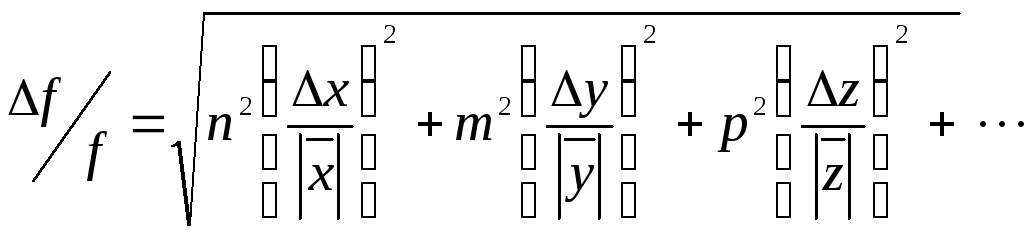26

В результате прямого измерения получается не истинное значение х измеряемой величины, а серия изn значений . Пусть теперь

Суммируя последнее равенство, получим

или

Но

(7)

где средне арифметическое измеренных значений. Таким образом,

(8)

Из этого простого результата вытекают весьма важные следствия. Действительно, при и.

значит, при бесконечно большом числе измерений и, следовательно, при конечныхn результат тем ближе к среднему арифметическому, чем больше число измерений. Отсюда также следует, что при оценке ∆Х в качестве целесообразно взять .

На практике n конечно и . В задачу математической теории случайной погрешности входит оценка интервала

(9)

в котором заключено истинное значение измеряемой величины. Интервал (9) называется доверительным интервалом, а величина –абсолютной погрешностью результата серии измерений. Теория оценки ∆х достаточно сложна, поэтому здесь будут рассмотрены лишь её основные результаты. Прежде всего нужно отметить, что, поскольку х – случайная величина, ошибка ∆х может быть определенна лишь с той или иной степенью надежности α, которую также называют доверительной вероятностью. Доверительная вероятность – это вероятность того, что истинное значение измеряемой величины х попадает в доверительный интервал (9). Если положить α=1 (100%), то это будет соответствовать достоверному событию, т.е. вероятности того, что х принимает какое-то значение в интервале (). При этом. Очевидно, такой выбор надёжностиα нецелесообразен. При малых α доверительный интервал ∆х определяется с малой достоверностью. В дальнейшем мы будем полагать α=0.90 или 0.95. Доверительный интервал и надёжность взаимосвязаны. Для оценки границ доверительного интервала английский математик В. Госсет (публиковавший свои работы под псевдонимом Стьюдент) ввёл в 1908 г. коэффициент:

(10)

равный отношению погрешности ∆х к средней квадратичной ошибке*

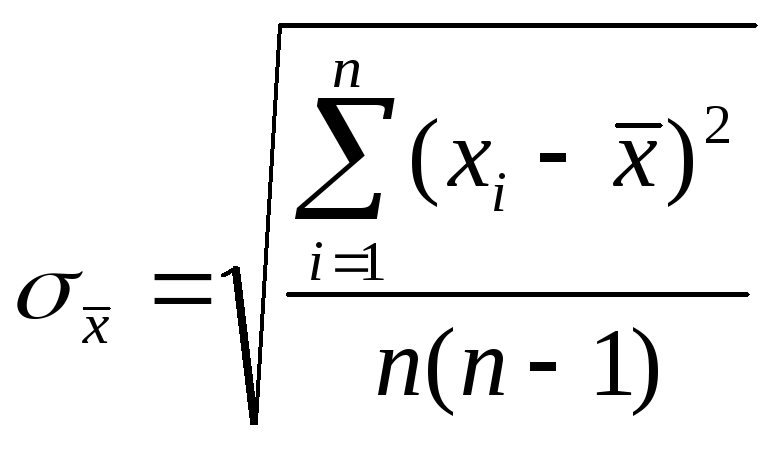(11)

Коэффициент зависит от надёжностиα, а также от числа измерений n и называется коэффициентом Стьюдента. Этот коэффициент табулирован (см. приложение 1), поэтому рассчитав и задав доверительную вероятностьα, нетрудно найти случайную ошибку:

(12)

Расчёт погрешности косвенных измерений.

При косвенных измерениях измеряемая величина f находится из функциональной зависимости:

где x, y, z – результаты прямых измерений. Формулу для ∆f можно получить, заменив в (2) дифференциалы погрешностями и взяв все слагаемые по модулю

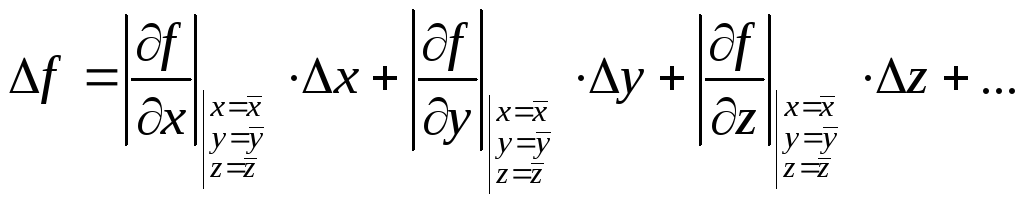(13)

Соотношение (13) рекомендуется для оценки погрешности ∆f , обусловленной приборными погрешностями величины x, y, z,… Для оценки погрешности, связанной со случайными ошибками прямых измерений, рекомендуется соотношение:

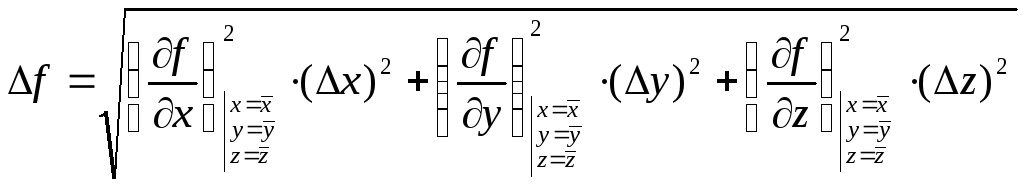(14)

Следует правда отметить, что формулы (13) и (14) приводят практически к одинаковым результатам. Производные в (13) и (14) берутся при средних, т.е. при измеренных значениях аргументов.

Очень часто функция f представлена степенной зависимостью от аргументов

(15)

где c, n, m и p – постоянные. Частным случаями формулы (15) являются соотнощения ,и др.

Задание. Покажите, что для функции вида (15) формулы (13) и (14) принимают вид:

(13)

(14)

Из соотношений (13) и (14) следует, что для степенных функций расчёт погрещностей существенно упрощается, причём целесообразно сначала найти относительную погрешность, которая выражается через относительную погрешность прямых измерений, а затем найти абсолютную погрешность

(16)

Под понимается функция от средних (измеренных) значений аргументов

.

Алгоритм расчета погрешностей

- Для прямых измерений

1. Вычислить среднее арифметическое результатов серии из n измерений:

Замечание: при расчете удобнее исходить из формулы:

где - любое удобное значение, близкое к.

2. Найти отклонения отдельных измерений от среднего значения

3. Исключить промахи.

4. Рассчитать среднюю квадратичную погрешность результата серии измерений

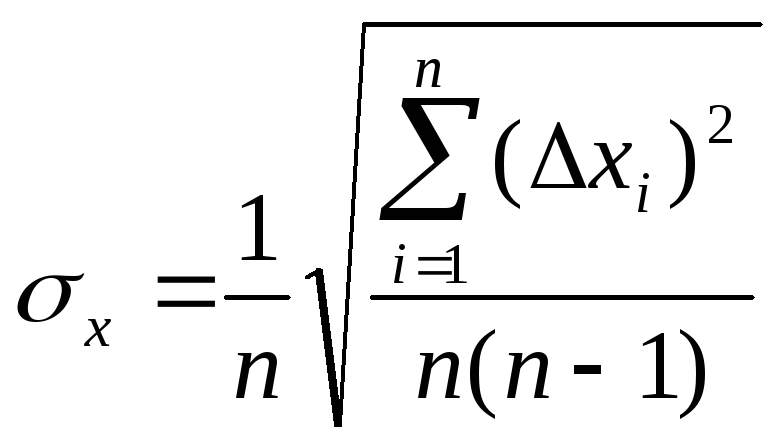
Замечание. При можно положить и рассчитывать по формуле

5. Если , то случайную ошибку можно не рас­считывать.

6. В противном случае задать доверительную вероятность и найти по таблице коэффициент Стьюдента .

7. Рассчитать границы доверительного интервала

Замечание 1. Если приборная погрешность имеет тот же порядок величины что и, то абсолютная погрешность результата серии измерений находится по формуле:

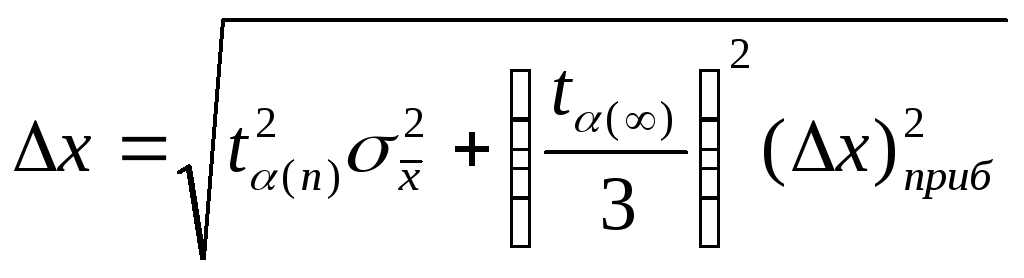
где Практически в качествеможно взять табличное значениеотвечающее самому большо­му из приведенных в ней значенийп (например, п=500 ).

Замечание 2. При большом числе измерений можно по­ложить

где .

8. Результат измерения представить в виде:

- Для косвенных измерений

Погрешность косвенного измерения можно рассчитать по одной из формул (13), (14), (13*), (14*). Две последние формулы выпол­няются для степенных зависимостей, а соотношения (13) и (14) име­ют общий характер.

Сводка соотношений для расчета погрешности косвенного измере­ния для некоторых простых функциональных за­висимостей представлена в таблице.

Таблица

Функция	Формулы для расчета погрешностей
	;
	;

Пример. Пусть джоулево тепло Q рассчитывается по формуле

Поскольку это степенная зависимость, целесообразно воспользоваться формулой (13*)

Правила представления результатов измерений и их погрешностей

Погрешности могут лишь оцениваться, поэтому обычно достаточно указать погрешность с одной значащей цифрой. Например, Δm=0,2 г. г. Запись т = 3,0 г означает, что измерение произведено с точностью до десятых долей грамма. Однако при про­межуточных вычислениях целесообразно оставлять больше значащих цифр.

Правила округления чисел (результатов измерений) иллюстрируют­ся в таблице (обратите внимание на особенности округления цифры 5).

Таблица Округление до десятых значащих цифр

До округления	После округления	Пояснения
734,7 736 735,0 745,0 745,1	730 740 740 740 750	4<5 6>5 3 – нечетное 4 - четное после 5 стоит не 0

Результат измерения принято округлять так, чтобы числовое зна­чение оканчивалось цифрой того же разряда, что и значение погреш­ности. Например, запись

см.

непреемлема, т.к. само значение погрешности Δl = 0,1 см указыва­ет на то, что цифры 018 результата не могут гарантироваться. Нуж­но записать так: см.