22 Потенциальная энергия заряда в поле другого заряда

Тело, находящееся в поле потенциальных сил, обладает потенциальной энергией, за счет которой совершается работа силами поля. Следовательно, работа может быть представлена как разность значений потенциальных энергий, которыми обладает заряд q' в точках 1 и 2 поля заряда q 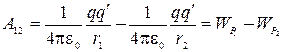Можно показать также, что, так как , . Отсюда для потенциальной энергии заряда в поле заряда q получаем: (6) Значение const в (6) обычно выбирают таким образом, чтобы при удалении заряда q' на бесконечность () потенциальная энергия обращалась в нуль. При этом условии получается, что (7) Будем считать q' пробным зарядом. Тогда потенциальная энергия, которой обладает пробный заряд, зависит не только от его значения , но и от значения q и r, определяющих поле. Следовательно, эта энергия может быть использована для описания поля, подобно тому, как была использована для этой цели сила, действующая на пробный заряд. Разные пробные заряды , будут обладать в одной и той же точке поля различной энергией , и т.д. Однако отношение будет для всех зарядов одно и то же. Величина (8) называется потенциалом поля в данной точке и используется наряду с напряженностью поля , для описания электрических полей. Как следует из (8) потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. Таким образом, для потенциального поля точечного заряда получаем следующее выражение: (9) Если поле создано системой точечных зарядов q1, q2, …, qn, находящихся на расстояниях соответственно r1, r2,…, rn до точки поля, в которой находится заряд , то работа, совершаемая силами этого поля над зарядом , будет равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности: . Но каждая из работ равна: 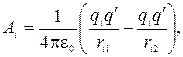где расстояние от заряда до начального положения заряда , расстояние от заряда до конечного положения заряда . Следовательно: . Сопоставляя это выражение с соотношением , получаем для потенциальной энергии заряда в поле системы зарядов выражение: , (10) откуда . (11). Следовательно, потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности. Из соотношения вытекает, что заряд , находящийся в точке поля с потенциалом , обладает потенциальной энергией . Следовательно, работа сил поля над зарядом может быть выражена через разность потенциалов: (12) Таким образом, работа, совершаемая над зарядом силами поля, равна произведению заряда на разность потенциалов в начальной и конечной точках. Если заряд из точки с потенциалом удаляется на бесконечность (где по условию потенциал равен нулю), работа сил поля будет равна или ,