Цифра / ЦОСиИ_2014_2015_заочн / ЦОСиИ_лаб_4

_{Лабораторная работа №}4. Проектирование не рекурсивных КИХ-фильтров при помощи весовых оконных функций и их программная реализация

Цель: расчет коэффициентов и исследование частотных и временных характеристик КИХ-фильтра.

Программное обеспечение: SCILAB, MS Visual Studio.

Теория

Цифровым фильтром называют аппаратную или программную реализацию математического алгоритма, входом которого является цифровой сигнал, а выходом – другой цифровой сигнал с определенным образом модифицированной формой и/или амплитудной и фазовой характеристикой.

Фильтр частотной селекции – это устройство, пропускающее или подавляющее частоты определенного диапазона в составе спектра входного сигнала. Существуют четыре основных типа фильтров частотной селекции: низкочастотный (НЧ), высокочастотный (ВЧ), полосовой (П) и режекторный (Р).

НЧ – фильтр пропускает все частоты ниже заданной частоты среза и подавляет частоты, превышающие другую заданную частоту - частоту среза зоны непрозрачности фильтра. Идеальную амплитудно-частотную характеристику (АЧХ) НЧ-фильтра можно представить в виде графика, показанного на рис.1.

Рисунок 1 – Идеальная АЧХ НЧ-фильтра

Должно выполняться условие . При этом, чем меньше разница между граничными частотами, определяющими рамки областей подавления и пропускания, тем больше показатель прямоугольности АЧХ:

(1)

а чем меньше , тем больше показатель узкополосности АЧХ фильтра:

(2)

где - частота дискретизации входного сигнала.

ВЧ – фильтр противоположен НЧ-фильтру по своим частотным свойствам. Он пропускает все частоты выше заданной частоты среза полосы пропускания и подавляет частоты ниже частоты среза зоны непрозрачности (рис.2).

Рисунок 2 – Идеальная АЧХ ВЧ-фильтра

Полосовой фильтр можно представить как последовательное соединение ВЧ- и НЧ-фильтров – он пропускает только определенную полосу частот и подавляет оставшуюся часть сигнала (рис.3). Это значит, что он характеризуется двумя частотами пропускания и двумя частотами подавления, и имеет соответственно две зоны подавления и одну пропускания.

Рисунок 3 – Идеальная АЧХ полосового фильтра

Режекторный фильтр – противоположность полосового. Он позволяет подавить частоты из определенного диапазона, пропуская на вход все остальные гармоники спектра сигнала (рис.4).

Рисунок 3 – Идеальная АЧХ режекторного фильтра

В таблице 1 представлены формулы для расчета идеальных импульсных характеристик фильтров различных типов ( - нормированные частоты краев полос пропускания или заграждения).

Таблица 1

 

Тип фильтра
Фильтр низких частот
Фильтр высоких частот
Полосовой фильтр
Режекторный фильтр

 

Идеальные характеристики фильтров не достигаются в реальности. Всегда существует погрешность, которая выражается в том, что коэффициент передачи фильтра в зоне непрозрачности не равен 0, а в полосе пропускания – не равен 1. На рисунке 4 иллюстрируется разница между идеальной и реальной АЧХ для НЧ фильтра.

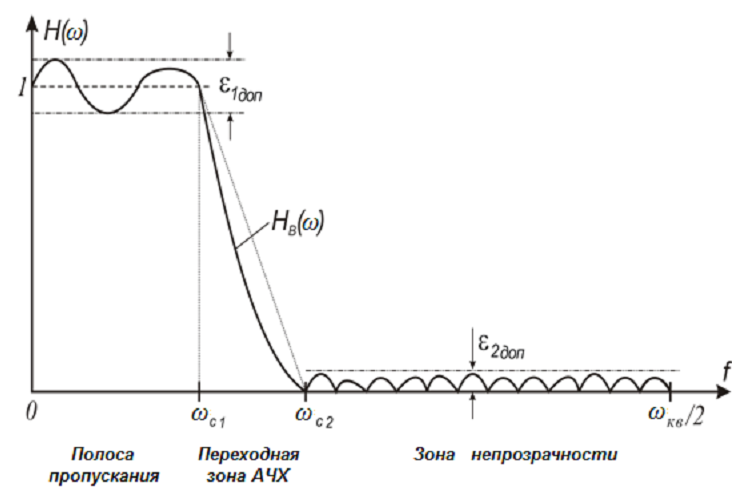
Рисунок 4 – Графики идеальной () и реальной () АЧХ фильтра

Поэтому перед тем, как начать проектирование фильтра, следует задать допустимые уровни погрешности воспроизведения желаемой АЧХ: - допустимая неравномерность АЧХ фильтра в полосе пропускания, - допустимый уровень боковых лепестков в зоне непрозрачности. Уровни допустимой погрешности воспроизведения желаемой АЧХ обычно задают в логарифмических единицах (децибелах). Так, подавление в зоне непрозрачности, равное 60 дБ = , означает ослабление выходного сигнала в 1000 раз, а неравномерность АЧХ в полосе пропускания 0,1 ДБ соответствует изменению его амплитуды не более чем в раз.

Итак, при разработке цифрового фильтра частотной селекции исходными данными являются:

- частота дискретизации - ;

- частоты среза полосы пропускания - , и частоты среза зоны непрозрачности - , (это справедливо для НЧ и режекторного фильтра; для ВЧ и полосового фильтра частоты среза меняются местами);

- допустимый уровень неравномерности АЧХ в полосе пропускания - (0,1-0,5 дБ);

- допустимый уровень боковых лепестков АЧХ в зоне непрозрачности - (40-120 дБ).

При этом порядок (память) КИХ-фильтра N можно оценить по следующей формуле [1]:

,

(3)

где L – логарифмический показатель частотной избирательности:

.

(4)

Разработать цифровой фильтр – значит получить его коэффициенты. В данной лабораторной работе рассматривается фильтр с конечной импульсной характеристикой (FIR – finite impulse response). Устройства такого типа при воздействии на них единичного импульса на выходе имеют конечное число ненулевых отсчетов . Чем больше порядок N, тем продолжительнее реакция фильтра. При этом вход и выход КИХ-фильтра связаны друг с другом выражением:

(5)

Высокий порядок фильтра требует больших вычислительных затрат и необходимых ресурсов емкости оперативной памяти. Однако чем больше порядок N, тем ближе реальные частотные характеристики к идеальным.

Порядок фильтра с идеальной АЧХ бесконечен. Поэтому при решении практических задач обработки сигналов импульсная характеристика должна иметь конечную длину. Наиболее простой способ получить конечную импульсную характеристику из идеальной бесконечной – умножить на весовую оконную функцию. Аналитически разработан целый ряд оконных функций, каждая из которых дает свое приближение к идеальной ЛАЧХ (логарифмическая АЧХ) фильтра. В таблице 2 приведены уравнения для весовых оконных функций, используемых в лабораторной работе.

Таблица 2

Название функции	Формула
Прямоугольное окно
Окно Хэмминга
Окно Хэннинга

Ход выполнения работы

1. Проектирование КИХ-фильтра и исследование его характеристик:

1. Используя формулу 3 и исходные данные (см. вариант задания) рассчитать порядок фильтра.

2. Средствами SCILAB получить коэффициенты фильтра , воспроизводящего желаемую частотную характеристику с заданной точностью (см. вариант задания) следующими оконными методами: прямоугольным, треугольным, Хэмминга, Хэннинга, Кайзера, Чебышева.

3. Построить АЧХ для каждого оконного метода и определить значения неравномерности АЧХ, уровень затухания в зоне непрозрачности, перерегулирования. Результаты занести в таблицу и выбрать наилучший оконный метод.

4. Для выбранного оконного метода увеличить, а затем уменьшить порядок фильтра на ±20. Рассмотреть, как изменяется АЧХ и характеристики фильтра. Сделать выводы.

1. Программная реализация фильтра:

   1. Используя теорему о свертке и данные, полученные в п.1 на языке С++ написать программу, осуществляющую фильтрацию 3 экспериментальных сигналов:

а) , где - частота среза полосы пропускания фильтра, - период дискретизации.

Для исследуемого сигнала убедиться, что при окончании переходного процесса (при n>N) на выходе фильтра формируется синусоидальный сигнал той же частоты и амплитуды.

б) , где - частота среза зоны непрозрачности фильтра.

Для исследуемого сигнала убедиться, что при окончании переходного процесса (при n>N) амплитуда выходного сигнала близка к нулю.

в) сигнал из лаб. раб. №1.

2.2. Проанализировать полученные результаты, сделать выводы.

Варианты индивидуальных заданий

№	Тип ЦФ	, Гц	Частота подавления, Гц	Частота пропускания, Гц	Уровень подавления (), дБ	Уровень пропускания, (), дБ
1	НЧ	1000	150	100	70	0,5
2	П	2000	150±100	150±50	40	0,5
3	ВЧ	1000	100	150	70	0,5
4	Р	2000	150±50	150±100	40	0,5
5	НЧ	1000	100	50	60	0,5
6	Р	2000	250±50	250±150	80	0,5
7	ВЧ	1000	50	100	60	0,5
8	П	2000	250±150	250±50	80	0,5
9	НЧ	1000	150	50	140	0,5
10	П	2000	175±125	175±25	70	0,5
11	ВЧ	1000	50	150	140	0,5
12	Р	2000	175±25	175±125	70	0,5
13	НЧ	1000	75	25	80	0,5
14	П	2000	200±125	200±50	60	0,5
15	ВЧ	1000	25	75	80	0,5
16	Р	2000	200±50	200±125	60	0,5
17	НЧ	1000	50	25	40	0,5
18	П	2000	250±225	250±150	60	0,5
19	ВЧ	1000	25	50	40	0,5
20	Р	2000	250±150	250±225	60	0,5
21	НЧ	1000	250	200	60	0,5
22	Р	2000	300±100	300±200	80	0,5
23	ВЧ	1000	200	250	60	0,5
24	П	2000	300±200	300±100	80	0,5

Контрольные вопросы:

1. Дайте определение следующих терминов: полоса пропускания, зона подавления, частота дискретизации, показатели частотной избирательности.

2. Дайте определение КИХ-фильтра.

3. Какие виды цифровых фильтров вы знаете?

4. Какие исходные данные необходимы для разработки цифрового фильтра?

5. В чем суть оконного метода расчета коэффициентов КИХ-фильтра?

Примеры и практические рекомендации

Расчет ВЧ КИХ-фильтра в SCILAB

// частота дискретизации сигнала 100 Hz

Fs = 100;

//временной интервал дискретизации

t = 0:1/Fs:1;

n = length(t);

f = linspace(0,Fs,n); // вектор частот

x1 = sin(2*%pi*1*t); // 1 Hz синусоида

x2 = sin(2*%pi*10*t); // 10 Hz синусоида

x = 2*x1 + x2; // Сумма 1 Hz и 10 Hz синусоид

plot(t,x); // представление сигнала во временной области

X = fft(x)./(length(x)/2); // спектр сигнала

plot(f(1:n/2),abs(X(1:n/2))); // вывод графика спектра сигнала

Пусть необходимо выделить 10 Гц синусоиду (подавить 1 Гц синусоиду). Для этого можно применить высокочастотный фильтр порядка N=21. Следующим шагом является определение частоты среза. В Scilab значение частоты среза нормируется на значение частоты дискретизации. Т. к. фильтруется дискретный сигнал, то возможные значения нормированной частоты среза принадлежат диапазону от 0 до 0,5. Тогда синусоиде с частотой 10 Гц при частоте дискретизации 100 Гц соответствует значение 0,1 (10/100), а синусоиде с частотой 1 Гц при частоте дискретизации 100 Гц соответствует значение 0,01 (1/100). Т. о. чтобы выделить один сигнал в другом можно для фильтра использовать частоту среза 0,07.

// синтез высокочастотного КИХ фильтра

[valcoeff, filtamp, filtfreq] = wfir ('hp', 21, [.07 0], 'hn', [0 0]);

Первый параметр ('hр') означает, что мы создаем фильтр высоких частот, второй (`21') - длина фильтра, а третий - частотой среза (для 'lр' и 'hp' необходимо использовать только первое значение). Значения частот нормируется на частоту дискретизации.

//построение импульсной характеристики фильтра и спектра сигнала

fr2 = filtfreq.*Fs;

plot(f(1:n/2),abs(X(1:n/2)),fr2,filtamp);

//plot(filtfreq, filtamp);

//вывод значений коэффициентов фильтра в командное окно

disp('Коэффициенты фильтра:')

disp(valcoeff);

Коэффициенты фильтра:

column 1 to 6

0. 0.0006309 0.0013987 - 0.0005885 - 0.0088300 - 0.0257518

column 7 to 12

- 0.0511616 - 0.0815882 - 0.1109208 - 0.1322131 0.86 - 0.1322131

column 13 to 17

- 0.1109208 - 0.0815882 - 0.0511616 - 0.0257518 - 0.0088300

column 18 to 21

- 0.0005885 0.0013987 0.0006309 0.

Для фильтрации сигнала после получения коэффициентов фильтра необходимо построить передаточную функцию.

//вычисление передаточной функции фильтра

hpoly = poly (valcoeff, 'z','coeff');

hz = horner (hpoly, (1/%z));

lisys = syslin ('d', hz);

// применение фильтра к сигналу

y = flts(x, lisys);

//вычисление спектра отфильтрованного сигнала

Y = fft(y)./(length(x)/2);

// вывод графика спектра отфильтрованного сигнала

plot(f(1:n/2),abs(Y(1:n/2)));

plot(t,y); // представление отфильтрованного сигнала во временной области

Литература

1. ЦОС. Часть 1: Методические указания к лабораторным работам/Рязанский гос. радиотех. университет./Сост: В.В Витязев, А.Ю. Линович, С.А. Якунин, Рязань, 2009.

2. Айфичер Э., Джервис Б. Цифровая обработка сигналов. Практический подход. / М., "Вильямс", 2004, 992 с.