Методы обработки изображений на основе математической морфологии
(mathematical morphology)
Ж. Серра и Ж. Матерон - начало 1970-х годов
Абламейко С.В., Лагуновский Д.М. Обработка изображений: технология, методы применение. - Минск: Институт технической кибернетики НАН Беларуси, 1999.-300с. стр. 84-86
Гонсалес Р., Вудс Р. Цифровая обработка изображений. – М: Техносфера, 2005. – 1072с. стр. 747-811
Тузиков Александр Васильевич. Математическая морфология, моменты, стереообработка: избранные вопросы обработки и анализа цифровых изображений / Тузиков А.В., Шейнин С.А., Жук Д.В.; Национальная Академия наук Беларуси, Объединенный институт проблем информатики.- Минск,2006.- 198 с
Методы обработки изображений на основе математической морфологии
Применяется для извлечения
некоторых компонент изображения, используемых при его представлении и описании:
границ, заданных областей, средних линий и др.
Математическая морфология (ММ)- использует язык теории множеств
Множества в ММ -объекты на
изображениях
Основные операции ММ
• наращение (расширение, дилатация) (dilation)
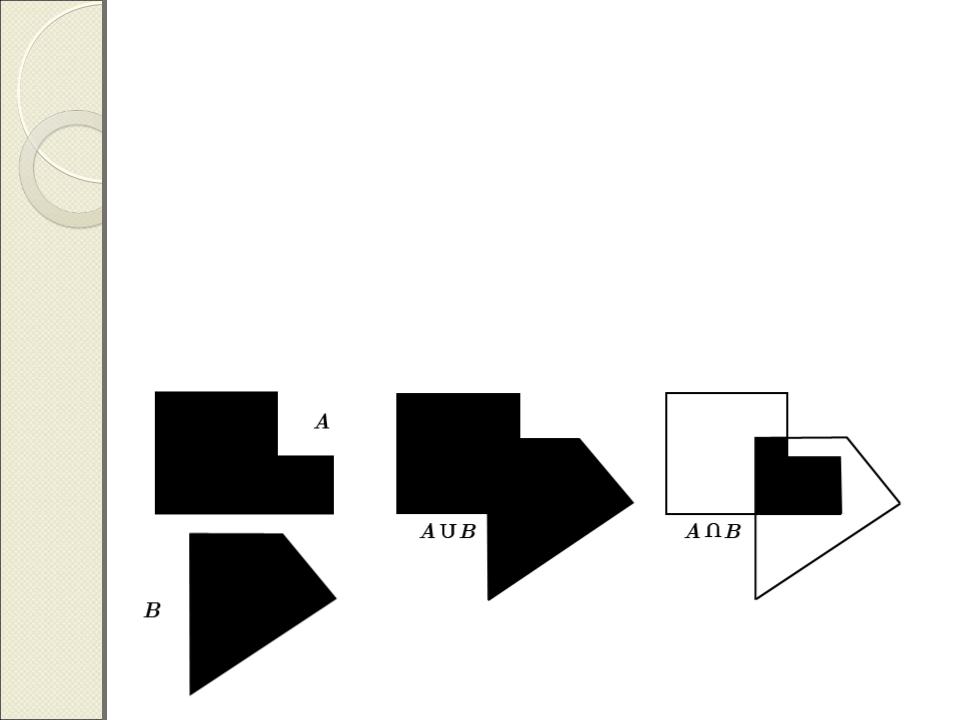
Обработка бинарных
изображенийДля бинарных изображений логические
операции взаимно однозначно соответствуют операциям над множествами
Операция пересечения – логическое умножение
A- множественное представление двоичного изображения
B - множество малого размера и простой формы (структурирующий элемент-structuring
element)
Операция расширения if A Z 2 & B Z 2
|
|
C Z 2 |
|
A B |
|
a A, b B:c=a+b |
g( j, k) a(m,n) b( j m 1, k n 1)
mn
, ло гические сум м иро ван ие и ум н о ж ен ие
mn
Пояснение операции «дилатация»
|
|
|
|
A |
|
|
|
B |
|
|
|
|
A B |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
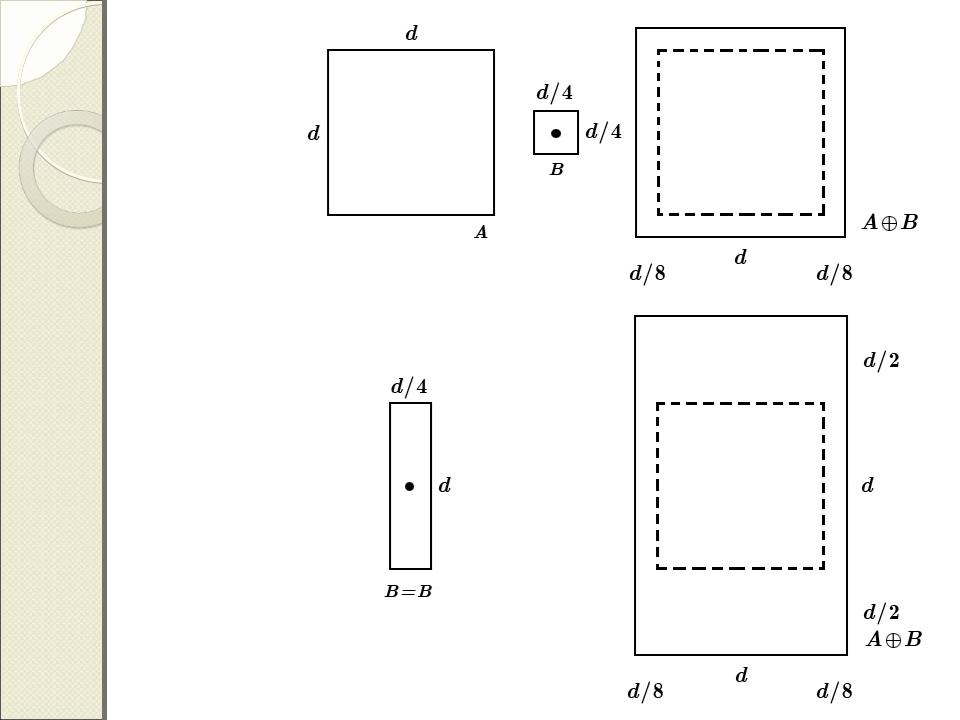
Влияние
формы
структур и- рующего элемента на результа
т
дилатаци
и
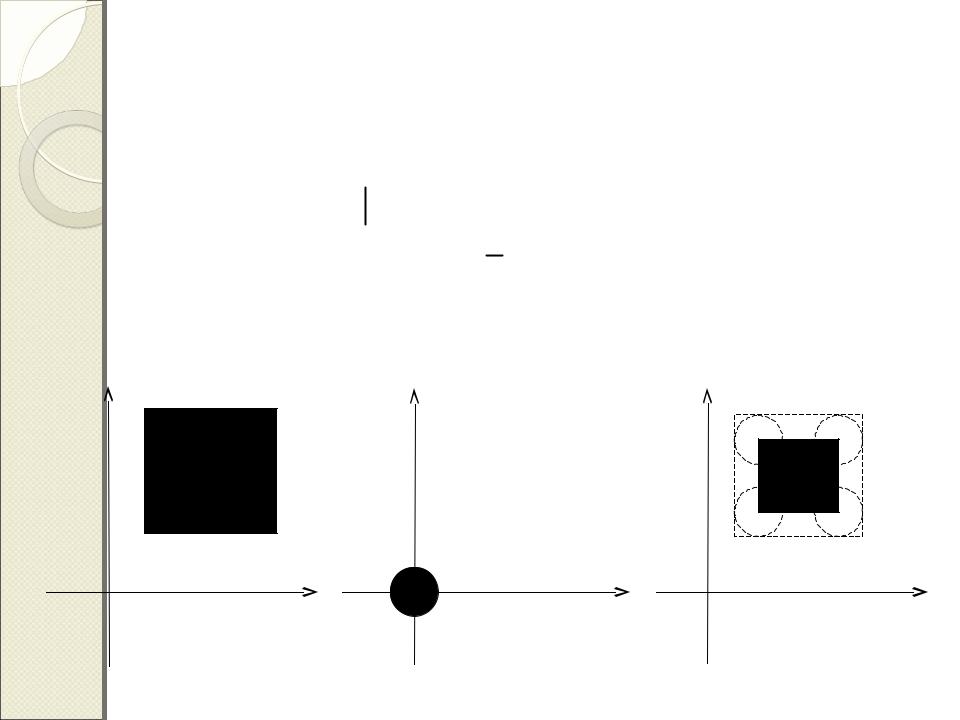
Операция
эрозии
if A Z 2 & B Z 2
A( )B C Z 2 b B,c+b A
g( j, k) a(m,n) b( j m 1,k n 1)
mn
A
B |
A(-)B |
|
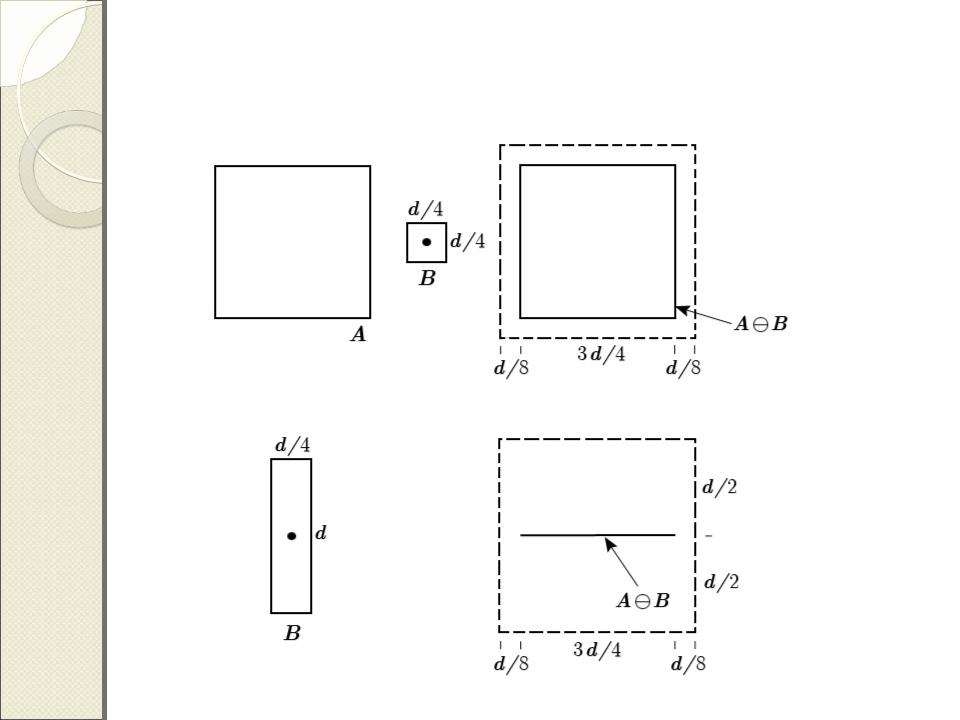
Влияние формы структурирующего элемента на результат эрозии
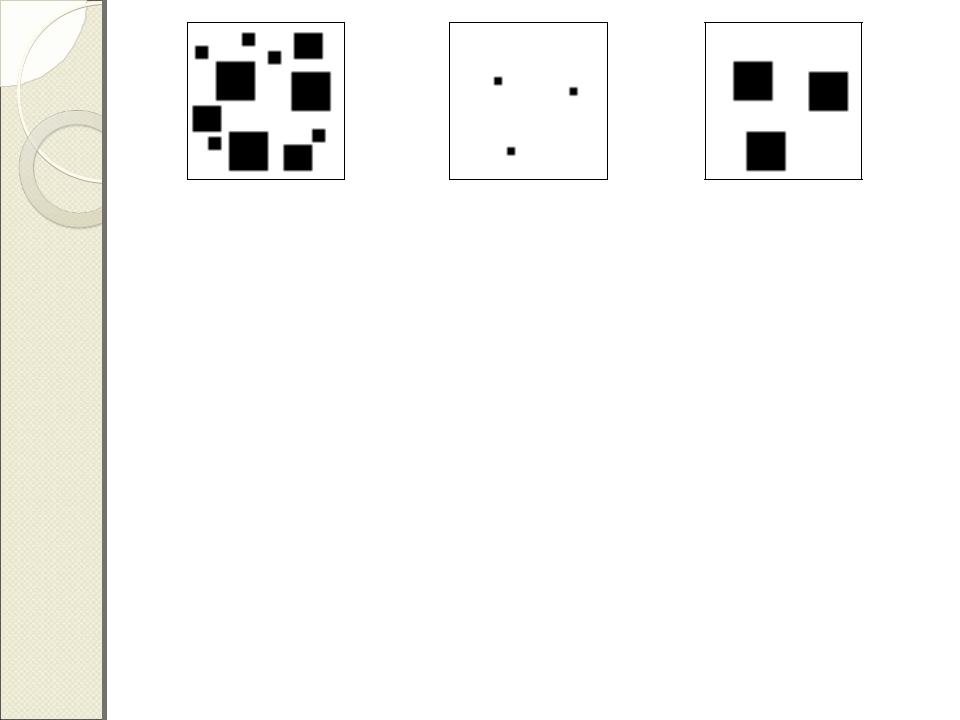
1 |
2 |
3 |
Исходное |
Результат |
Результат |
Изображение |
эрозии 1, квадрат, 13*13 |
дилатации 2 |
|
|
квадрат, 13*13 |
1.Дилатация не позволяет полностью восстанавливать объекты после эрозии
2.В изображении остаются лишь те симметрии, которые присутствуют в структурирующем элементе.
3.Структурирующий элемент должен быть близок к кругу (симметричен по всем направлениям).
4.Используются два способа представления объектов: черные и белые - активные пиксели структурирующего элемента принимают те же двоичные значения, что и интересующие объекты