2.4.2. Расчёт обобщённой инертности масс станка.

Инертные свойства машин и механизмов характеризуют приведённой массой, либо приведённым моментом инерции подвижных звеньев, в зависимости от того, линейным или угловатым является перемещение звена приведения.

Приведённый к звену момент инерции масс других, связанных с ним звеньев, вычисляют как сумму произведений масс этих звеньев и их моментов инерции на квадраты её передаточных функций в движениях этих звеньев относительно звена приведения.

Приведённый к звену механизма момент инерции масс других его звеньев может быть переприведён, например, к главному валу машины, для чего его величину следует умножить на квадрат передаточной функции от звена приведения механизма к указанному валу.

Т.о., приведённый к валу кривошипа ОА – принимаем его за главный – момент инерции масс звеньев станка можем представить как сумму приведённых моментов инерции трёх его механизмов - зубчатой передачи, механизма поперечной подачи стола и несущего механизма - и двух деталей – ротора приводного электродвигателя и махового колеса.

Вычислим приведённые моменты инерции указанных механизмов и деталей.

1. Для ротора приводного электродвигателя имеем:

.

2. Для зубчатой передачи имеем:

,

где - приведённый к валу водила момент инерции планетарного механизма:

,

где К – число сателлитов.

Передаточная функция:

Остальные данные берём из табл. 2.6.

Получаем:

При этом:

3. Приведённый к валу кривошипа момент инерции механизма поперечной подачи стола влияет на движение станка лишь в периоды движения толкателя кулачкового механизма – на фазах удаления и возвращения. Причём, на концах этих фазт.к. передаточная функцияот толкателя к кулачку, т.е. к валу кривошипа ОА, при этом равна нулю.

Максимальное значение приобретает вблизи середины этих фаз, когда.

В этом положении величина приведённого момента инерции механизма поперечной подачи может быть приведена к виду:

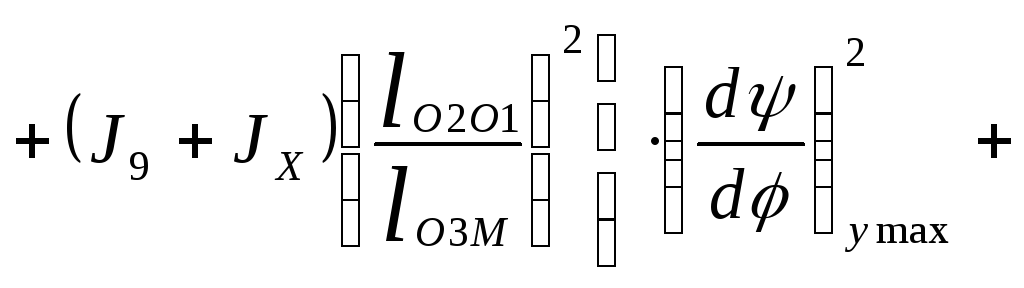
4. Для приведенного к валу входного кривошипа ОА момента инерции несущего механизма можем составить выражения:

где передаточная функция в движении ползуна (резцедержателя) 5 относительно кривошипа ОА может быть вычислена как:

.

Составим алгоритм вычисления передаточных функций.

Ранее получены размеры звеньев шарнирного четырехзвенника ОАВD, массы и момента инерции.

, ,,

, ,

,

рис. 2.5

Непосредственно из рис. 2.5. находим:

Далее получим:

Таблица 2.7

N
0 1 2 3 4 5 6 7 8 9 10 11	151 196 254 268 270 298 326 6 31 51 90 111	0 39 77 88 90 118 126 158 180 204 270 322	0 15 23 25 25 22 19 9 0 -9 -25 -15	1,43 1,26 1,02 0,93 0,89 -0,37 -0,38 -0,41 0,61 0,8 0,89 1,3	0,86 1,002 1,05 1,33 1,48 0,75 0,26 -0,12 -0,26 -0,34 -0,46 -0,38	-0,114 0,095 0,719 0,792 0,832 0,575 0,242 -0,029 -0,003 -0,177 -0,603 -0,2	0 0,062 0,109 0,12 0,12 0,078 0,068 0,031 0 -0,034 -0,38 -0.044

где

а угол кривошипа ОА замеряем непосредственно из плана положений.

Результаты расчётов заносим в таблицу 2.7.

Данные табл. 2.7. В одном из положений механизма проверяем при помощи планов положений и скоростей, затем используем для вычисления приведенного к валу кривошипа О его момента инерции, где - угол поворота кривошипа ОА от своего начального положения, соответствующего одному из кратчайших положений резцедержателя. Величина его вычислена как, где- угол кривошипа ОА со стойкой ОС в нулевом положении механизма.

В табл. 2.8. определено:

_,

Значения приведенного момента инерции станка в различных его положениях вычисляем как:

Постоянная , составляющая приведенного момента инерции станка.

- переменная его составляющая.

На листе 1 строим диаграмму энергомасс – зависимость от. С помощью этой диаграммы находим момент инерции постоянной составляющей маховых масс, при которой частота вращения приводного электропривода станка за цикл установившегося движения изменяется соответственно допустимому коэффициентуизменения средней скорости хода.

Таблица 2.8.

Положение кривошипа ОА	Значение обобщённой координаты 10	Работа сил		Приращение кинетической энергии Ti	Момент инерции, приведённый к главному валу станка (валу кривошипа АО (кг·м2)
		Движущих АДВ (кДЖ)	Сопротивлений АС (кДЖ)
0	0	0	0	0	0,19486	0,39202	0,0081	0,002477
1	39	0,052	0	0,052	0,19486	0,39202	0	0,016858
2	77	0,102	0,14	-0,038	0,19486	0,39202	0	0,029172
3	88	0,11	0,14	-0,03	0,19486	0,39202	0	0,031362
4	90	0,12	0,16	-0,04	0,19486	0,39202	0	0,036537
5	117	0,15	0,33	-0,18	0,19486	0,39202	0	0,026086
6	126	0,16	0,33	-0,17	0,19486	0,39202	0	0,024346
7	156	0,208	0,48	-0,272	0,19486	0,39202	0	0,011466
8	180	0,24	0,48	-0,24	0,19486	0,39202	0	0,010888
9	203	0,27	0,48	-0,21	0,19486	0,39202	0	0,02142
10	270	0,36	0,48	-0,12	0,19486	0,39202	0	0,036537
11	321	0,42	0,48	0,06	0,19486	0,39202	0	0,027767
0	360	0,48	0,48	0	0,19486	0,39202	0,0081	0,002477

Такое ограничение необходимо для предохранения приводного электродвигателя от перегрева, для повышения общего КПД работы станка за счет снижения получаемого тепла обмотками электродвигателя. Предполагая незначительную занятость строгальных станков на производстве, в соответствии принимаем:

Средняя угловая скорость вала кривошипа ОА:

Углы наклона касательных к диаграмме энергомасс (рис. 2.6) определяем по формулам:

где ;- масштабы приведённого момента инерции и энергии, выбранные для диаграммы энергомасс.

После подстановки чисел получаем:

откуда

, .

Проведя касательные к диаграмме под указанными углами к оси , находим отрезки О₁К и О₁l (в мм), которые используем для определения начала координат О системы - зависимости полной кинетической энергии движущихся звеньев станка от их момента инерции приведенного к главному валу (О₁К = 20 мм; О₁l = -150 мм.).

Уравнения касательных:

решаем совместно: вычитанием второго уравнения из первого получим:

после чего из первого уравнения получим:

.

Из рис.2.6: видно, чтобы перейти от системы координат к системе, из начала О которой диаграмма энергомасс видна под угламиинеобходимо к переменной части момента инерции станка прибавить постоянную часть:

.

Часть этого момента инерции в проектируемой схеме поперечно-строгального станка уже имеется (за счёт ротора электродвигателя и зубчатого механизма). Остальную часть:

водим в состав станка в виде дополнительной маховой массы – махового колеса. Если диаметр этого колеса принять D_max = 1.0 м, а массу распределить по его ободу, то она составит

.

Большие вес и габариты маховик обуславливают необходимость закрепления его на более быстроходном валу.

При закреплении маховика на валу электродвигателя его момент инерции будет составлять

и при радиусе, например, R_max= 100 мм он будет иметь массу:

.

Такой маховик запасает кинетическую энергию: