2.4.2. Расчёт обобщённой инертности масс станка.

Инертные свойства машин и механизмов характеризуют приведённой массой, либо приведённым моментом инерции подвижных звеньев, в зависимости от того, линейным или угловатым является перемещение звена приведения.

Приведённый к звену момент инерции масс других, связанных с ним звеньев, вычисляют как сумму произведений масс этих звеньев и их моментов инерции на квадраты её передаточных функций в движениях этих звеньев относительно звена приведения.

Приведённый к звену механизма момент инерции масс других его звеньев может быть переприведён, например, к главному валу машины, для чего его величину следует умножить на квадрат передаточной функции от звена приведения механизма к указанному валу .

Приведённый к главному валу машины момент инерции её маховых масс может быть вычислен как сумма произведений приведённых моментов инерции её механизмов (и одиночных звеньев) на квадраты передаточных функций при движении звеньев приведения относительно вала машины, принятого за главный.

Т.о., приведённый к валу кривошипа ОА (рис.1.1) – принимаем его за главный – момент инерции масс звеньев станка можем представить как сумму приведённых моментов инерции трёх его механизмов - зубчатой передачи, механизма поперечной подачи стола и несущего механизма - и двух деталей – ротора приводного электродвигателя и махового колеса.

Вычислим приведённые моменты инерции указанных механизмов и деталей.

1. Для ротора приводного электродвигателя имеем:

.

2. Для зубчатой передачи имеем:

,

где -приведённый к валу водила момент инерции планетарного механизма, а величинувычисляем, пользуясь рис. 2.10:

.

ЗдесьK – число сателлитов.

Передаточная функция: а- получено ранее.

Остальные данные берём из табл. 2.6.

Получаем:

При этом:

3. Приведённый к валу кривошипа момент инерции механизма поперечной подачи стола влияет на движение станка лишь в периоды движения толкателя кулачкового механизма – на фазах удаления и возвращения. Причём, на концах этих фазт.к. передаточная функцияот толкателя к кулачку т.е. к валу кривошипа ОА, при этом равна нулю.

Максимальное значение приобретает вблизи середины этих фаз, когда, коромыслаMN и KL параллельны, вследствие чего передаточная функция от второго коромысла к первому также приобретает своё максимальное значение. В этом положении величина приведённого момента инерции механизма поперечной подачи может быть вычислена из выражения:

Отсюда после несложных преобразований получаем :

где - есть передаточная функцияот коромыслаKL к коромыслу BM, когда KL // MN и МЦС шатуна LN расположен в бесконечности.

4. Для приведенного к валу входного кривошипа ОА момента инерции несущего механизма (рис. 2.11) можем составить выражения:

Рис.2.2. Кулисный механизм

Для контура COAC векторному уравнению замкнутости соответствуют уравнения

Из этих уравнений можно получить формулы для определения угловой координаты кулисы 3 и отрезка:

Передаточное отношение

Значения координаты - угла кривошипа ОА с направлением стойки ОС – замеряем транспортиром непосредственно из плана положений механизма (чертёж 2, приложения 3).

Результаты расчётов заносим в таблицу 2.7.

Данные таблицы 2.7 (линейные и угловые перемещения) должны быть в согласии с планом положений несущего механизма (приложение 1), а для согласованности программы вычисления передаточных функций в одном из положений механизма можно построить план скоростей (приложение 3).

Таблица 2.7
№ поло-жения мех-ма
0	-30	60	0
1	20	68	0.27
2	39	73	0.31
3	90	90	0.34
4	124	101	0.32
5	162	112	0.26
6	210	120	0
7	296	68	-0.59
0	330	60	0

Таблицу 2.7. используем для вычисления приведенного к валу кривошипа АО (главному валу станка) приведённого момента инерции (табл. 2.8). В эту же таблицу для различных положений станка заносим значения приведённых моментов инерции масс других, вычисленных ранее деталей и механизмов.

Таблицу 2.8. используем для определения недостающей массы – маховика.

Таблица 2.8.

Положение кривошипа ОА	Значение обобщённой координаты 10	Работа сил		Приращение кинетической энергии Ti	Момент инерции, приведённый к главному валу станка (валу кривошипа АО (кг·м2)
		Движущих АДВ (кДЖ)	Сопротивлений АС (кДЖ)
0	0	0	0	0	0.78	6.15	0.63	0.467
1	50	0.082	0	0.083	0.78	6.15	0	0.508
2	69	0.115	0.082	0.026	0.78	6.15	0	0.514
3	120	0.200	0.167	-0.117	0.78	6.15	0	0.519
4	154	0.257	0.380	-0.243	0.78	6.15	0	0.517
5	192	0.320	0.516	-0.280	0.78	6.15	0	0.507
6	240	0.400	0.638	-0.200	0.78	6.15	0	0.467
7	326	0.543	0.720	-0.057	0.78	6.15	0	0.375
0	360	0.600	0.720	0	0.78	6.15	0.63	0.467

5. Масса маховика имеет ту особенность, что будучи оформленной в виде махового колеса (желательно с тяжёлым ободом, т.к. при этом она минимальна) величина её постоянна. Приведённый к главному валу О момент инерции махового колеса определяем, строя для всех движущихся масс станка диаграмму энергомасс () – зависимость приведённого момента инерции движущихся масс () от, запасаемой этими массами энергииТ.

Вначале в осях приращений установим форму указанной диаграммы, затем найдём положение осейполных значений энергии станкаТ и необходимого приведённого момента инерции. По координатам начала этих осей в системе координат вычислим инертную массу, которую необходимо добавить для получения динамической устойчивости выполняемого техпроцесса.

Динамическую устойчивость машинного техпроцесса оценивают коэффициентом неравномерности вращения главного вала (станка) (/2/ табл. 5.2), который указанную устойчивость обеспечивает путём защиты приводного электродвигателя от перегрузок и, гарантирует получение изделий надлежащего качества.

Согласно указанному, вычислим приращения кинетической энергии , подвижных масс станка, за цикл установившегося движения:

. (2.21)

Вначале методом интегрирования графика нагрузок – зависимости сил полезного сопротивления () от хода рабочего звенаН (прямого и обратного) получаем график работ полезных сил (чертеж 1, приложения3):

.

Из этого графика находим значения в различных (характерных) положениях станка (его главного вала).

Результаты заносим в табл. 2.8. В табл. 2.8. также заносим значения , которые получаем на основании того, что функцияпрямая пропорциональность^.

Поэтому:

,

где (в первом приближении) работу движущих сил за цикл () можем приравнять ранее установленной работе сил полезных сопротивленийза это же время:

.

Результат для для различных положений станка заносим в табл. 2.8.

Величину приведённого момента инерции масс станка в различных его положениях () представим в виде суммы постоянной () и изменяемой () составляющих:

,

где включает неизвестную маховую массу, сосредоточенную в маховике, а- обобщает изменяемые маховые массы.

Считаем, в рассматриваемом примере:

,

а ,

где - приведенный к главному валу 9 момент инерции маховика.

Строим диаграмму и проводим к ней касательные

под углами (/2/ стр. 371):

где ;- масштабы приведённого момента инерции и энергии, выбранные для диаграммы энергомасс,(табл. 5.12 /2/ стр. 369), а средняя угловая скорость главного вала.

После подстановки чисел получаем:

откуда

, .

Проведя касательные к диаграмме под указанными углами к оси , находим отрезки О₁К и О₁l (в мм), которые используем для определения начала координат О системы - зависимости полной кинетической энергии движущихся звеньев станка от их момента инерции приведенного к главному валу (О₁К = 78.2 мм; О₁l = -284.7 мм.).

Уравнения касательных:

решаем совместно: вычитанием второго уравнения из первого получим:

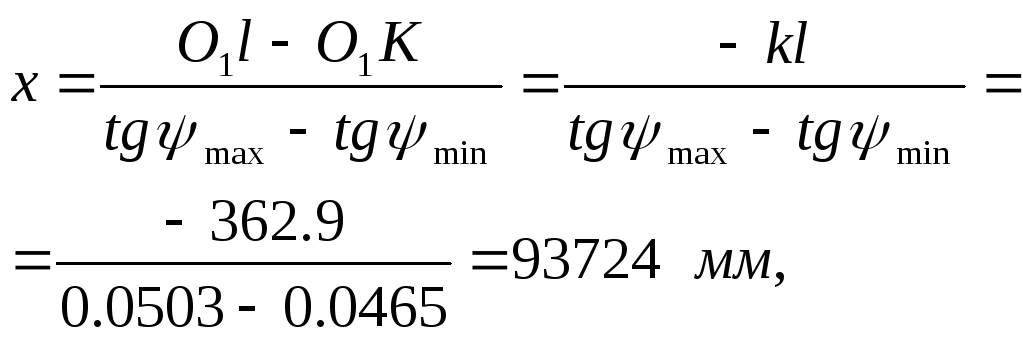
после чего из первого уравнения получим

.

Из рис.2.11: видно, чтобы перейти от системы координат к системе, из начала О которой диаграмма энергомасс видна под угламиинеобходимо к переменной части момента инерции станка прибавить постоянную часть:.

Часть этого момента инерции в проектируемой схеме поперечно-строгального станка уже имеется (за счёт ротора электродвигателя и зубчатого механизма). Остальную часть:

вводим в состав станка в виде дополнительной маховой массы – махового колеса. Если диаметр этого колеса принять D_МАХ = 1.0 м, а массу распределить по его ободу, то она составит .

Большие вес и габариты маховика обуславливают необходимость закрепления его на более быстроходном валу.

При закреплении маховика на валу электродвигателя его момент инерции будет составлять

и при радиусе ,например, R_МАХ = 100 мм он будет иметь массу

.

Такой маховик запасает кинетическую энергию: