2.3.2. Проектирование винтового и храпового механизмов.

При повороте коромысла О₁О₂ (рис. 2.7) на угол , храповик находится в зацеплении с собачкой , сидящей на коромысле О₃М, и должен быть повёрнут на угол , соответствующий перемещению маточной гайки (стола) в направлении оси О₃ на величину мм.

Выбрав в качестве ходового винт с диаметром Ø24 мм с трапецеидальной резьбой по СТ СЭВ 185-79 Tr 24×10 (Р5), получаем:

(2.11)

где h^* = 10мм – ход винта (по СТ СЭВ 185-79).

Чтобы обеспечить надёжный перехват собачкой зубцов храповика, угол поворота коромысла МО₃ принимаем несколько большим:

Найдём размеры храпового колеса. В соответствии со стр. 191 /7/, число зубцов храповика

,

где K₁ – минимальное целое число, при котором так же получается целым.

Преобразуем формулу (2.11) к виду:

,

а после умножения обеих частей на будем иметь:

.

На основании (2.12) приходим к выводу, что

и что - минимальное целое число, на которое необходимо умножать отношение, чтобы результат получился целым. Таким числом в нашем случае является:

.

Задавшись модулем храпового колеса (СТ СЭВ 185-79):

,

получаем делительный диаметр

мм.

2.3.3. Синтез качающейся кулисы привода собачки.

Указанный кулисный механизм проектируем графическим способом по известным входному () и выходному () углам, а так же положению центра вращения одного его коромысла (О₂L).

Для этого:

1. На плане положений несущего механизма (чертеж 1 приложения 3) в свободном, не пересекаемом звеньями месте, выбираем положение центра L оси ходового винта.

2. Из условия удобного размещения оси собачки храпового механизма задаёмся длиной коромысла LK: (). Изображаем коромыслоLK в двух крайних его положениях так, чтобы угол K₁LK₇ составил ().

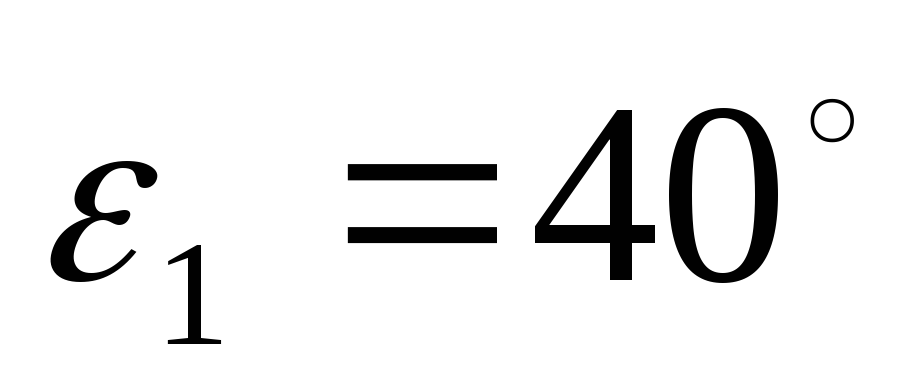3. Задаёмся длиной OB_min=R_min и OB_max=R_min .

4. Из плотной бумаги изготавливаем шаблон в виде сектора семейства концентрических окружностей (рис. 2.9). центральный угол этого сектора равен углу размаха коромыслаBM кулачкового механизма (). Помещая вершину этого сектора вдоль горизонтальной линии равностоящей отR_min и R_min . Подбираем такую дугу, из указанного семейства, концы которой разместятся на дугах, проведённых из центров B_min и B_max по п. 3. Радиус этой дуги () составляет длину коромыслаBM.

5. Примем KN =0,13(м). тогда методом засечек определим положение звена KN.

6. Исходя из построений синтеза качающейся кулисы примем MN`=0,25.

2.4. Динамический синтез станка (расчет ориентировочной его массы и энергии при запуске).

Динамический синтез станка позволит обеспечить динамическую устойчивость выполнения заданной технологии, повысить к.п.д. путём снижения теплового излучения обмоток приводного электродвигателя вследствие неравномерного вращения ротора внутри цикла.

Задачу решают подбором и перераспределением масс звеньев, при необходимости вводят дополнительную маховую массу с постоянным моментом инерции в виде маховика /8/. Произведём учет инертных свойств звеньев используемых механизмов.

2.4.1. Расчёт масс и моментов инерции звеньев и механизмов.

Инертные свойства звеньев характеризуют показатели массы (при поступательном движении) и момента инерции при вращательном.

В первом приближении можно принять, что по длине рычагов массы распределены равномерно, что интенсивность их распределения (/1/ стр. 240), что зубчатые колёса – сплошные диски с шириной, зависящей от межосевого расстоянияa_w, как

,

где (/5/ стр. 180) представляет собой коэффициент ширины зуба. При этом центры масс рычагов располагаются по их серединам, массы определяются как

,

моменты инерции относительно центров масс как

(/10/ стр. 335),

а относительно оси вращения (для вращающихся звеньев) как:

.

Массы зубчатых колёс определяем через делительные диаметры и межосевые расстояния по формуле

,

которая при плотности материала (сталь, чугун) ипринятом коэффициенте ширины зуба /5/, для облегчения вычислений предварительно должна быть приведена к виду:

,

где ивм., а - вкг.

Моменты инерции зубчатых колёс относительно оси вращения определяем через их массу и делительный диаметр как для однородных дисков:

(/10/ стр. 336).

Результаты расчётов заносим в табл. 2.6.

Оценку динамических характеристик прочих деталей станка производим следующим образом:

1. Массу резцедержателя вместе с перемещающим его ползуном оцениваем приблизительно как^: .

2. Массу стола и закреплённой на нём детали ориентировочно оцениваем как: .

3. Массу водила планетарной ступени редуктора находим с помощью формулы,

где ширину водила «» принимаем равной толщине смонтированного в нем сателлита,

т.е. .

С учётом этого ,

а момент инерции (как для сплошного диска):

.

4. Массу храпового колеса определим как:

,

где диаметр храпового колеса

,

а ширину принимаем равной

.

С учётом этого

,

а момент инерции

.

5. Массу кулачка и момент инерцииоцениваем по среднему его радиусу:

и ширине , которую задаём как

.

В этом случае

,

а момент инерции

.

6. Момент инерции ротора электродвигателя определяем по его маховому моменту

.

Получаем: ;

масса двигателя (табл. 2.1.).

7. Динамические характеристики остальных движущихся звеньев – ходовой винт, валы, ролик кулачкового механизма и т.п. из-за малых масс, либо скоростей точек, считаем пренебрежимо малыми и далее не учитываем.

Полученные в п.п. 1-6 данные так же заносим в табл. 2.6. и используем при последующем динамическом синтезе машины.

Таблица 2.6

Наименование звена	Обозначение звена	Наименование параметра и его обозначение
		Длина рычага, диаметр колеса, (м)	Масса звена, (кг)	Момент инерции относительно оси вращения , (кгм2)	Момент инерции относительно центра масс, (кгм2)
Рычаг (рис. 2.3., 2.7.)	ОOA		m1 = 0.45	J 1= 3.4·10-3	
	АCT		m2 = 1.5	J2 = 1.25·10-1	
	CCD		m3 = 0.9	J3 = 2.7·10-2	
	OO1O2		m6 = 3.60	J6 = 1.73·10-2	
	OO2K		m7 = 2.85	J7 = 8.57·10-3	
	KKM		m8 = 5.10		JS8 = 1.23·10-2
	MMO3		m9 = 1.80	J9 = 2.16·10-3	
Зубчатое колесо рис.2.1.	Z1 Z2 Z4 Z5	d1 = 0.036 d2 = 0.096 d4 = 0.080 d5 = 0.36	mZ1 = 0.131 mZ2 = 0.932 mZ4 = 1.152 mZ5 = 8.65	JZ1 = 2.12·10-5 JZ2 = 1.07·10-3 JZ4 = 9.21·10-4 JZ5 = 4.5·10-1	Как и относительно оси вращения //
Ползун (рис.2.10.)	A Е Т	  			//
Водило H (рис.2.1.)	HН				//
Кулачёк (рис.2.7.)					//
Храповое колесо (рис.2.7.)					//
Ротор эл. Двиг. 8 (рис1.1)					//