2.3. Синтез механизма поперечной подачи стола.

Во время перебегов резца в конце холостого и начале рабочего ходов происходит перемещение стола с обрабатываемой деталью при помощи ходового винта. Поворот винта производиться посредством передаточного механизма, состоящего (рис. 2.2) из храпового колеса 9, рычага с собачкой , тяги 7 и качающегося толкателя 6. Поворот толкателя осуществляется дисковым кулачком, закреплённым на кривошипном валу 0.

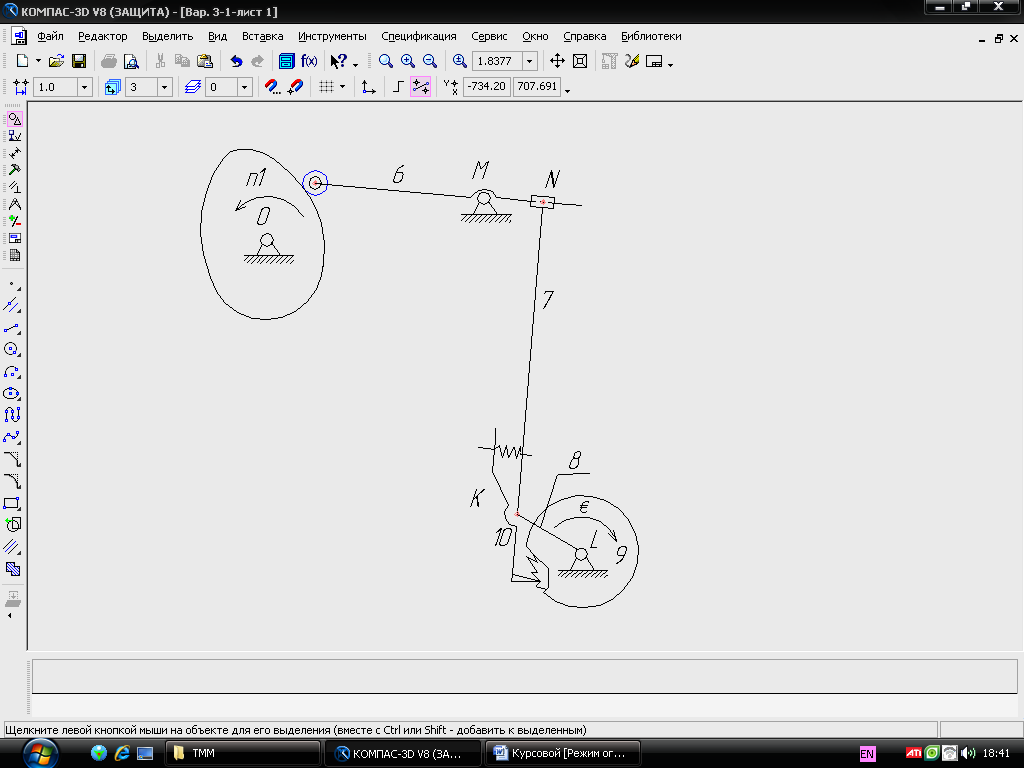
Рис.2.2. Схема механизма поперечной подачи стола

Рассмотренный сложный передаточный механизм (рис. 2.2) представим как совокупность четырёх простых механизмов:

1. кулачкового, включающего кулачек и коромысло;

2. винтового, состоящего из ходового винта, расположенного вдоль оси, и маточной гайки (не показана), закрепляемой на столе;

3. храпового, включающего храповое колесо, жестко связанное с ходовым винтом, рычага, собачки шарнирно закрепляемой на рычаге с возможностью поворота на угол относительно оси ходового винта ;

4. Кулисный механизм ОCDE.

Найдём размеры этих механизмов:

2.3.1. Синтез кулачкового механизма.

В описании прототипа указано, что фазовый угол возвращения коромысла может быть равен фазовому углу удаления, причём эти углы разделены между собой фазовым углом дальнего стояния; при повороте кулачка на уголмеханизм подачи стола фиксируется в одном из своих крайних положений.

Вычертив 1-е и 7-е положения несущего механизма методом засечек, начиная от ползуна A, замеряем с помощью транспортира угол давления и строим положения 2 и 5 несущего механизма, соответствующие окончаниям фаз дальнего стояния (принято) и возвращения (принято).

Из таблиц, помещённых в описании прототипа (/Ι/ стр. 239) следует, что длина коромысла может быть принята в интервале м., а угол качания.

Принимаем м.,.

Выбираем закон движения толкателя кулачкового механизма на фазах удаления и возвращения. Поскольку кулачковый механизм со столом станка (звено, обладающее значительной массой) связан посредством храпового механизма, а тот в начале и конце зацепления храповика с собачкой имеет «жесткие удары», по времени совпадающие с началом и концом фазы удаления в кулачковом механизме, то с целью более успешного противостояния^ этим ударам, на фазе удаления выбираем безударный закон, например, с изменением ускорения по синусоиде, треугольнику, либо трапецеидальный (см. законы 5,6 и 7, в табл. 2.10 /Ι/).

На фазе возвращения коромысла кулачёк не имеет кинематической связи с массивным столом станка и силы инерции стола на него не воздействуют. Поэтому на указанной фазе можем применить более простые законы, в том числе, такие, которые имеют «мягкий удар». Среди них, например, модифицированный линейный закон, косинусоидальный, с равномерно убывающим ускорением и т.п.

Для нашей конструкции станка применяем гладкие законы – синусоидальный на фазе удаления и с равномерно - убывающим ускорением на фазе возвращения (рис. 2.8). При прочих равных условиях () эти законы обеспечивают приемлемую величину максимума ускорения (например, при изменении ускорения по треугольнику значение этого максимума значительно больше – см. табл. 2.10 /1/).

РИС 2.8. Закон движения коромыслового толкателя кулачкового механизма

Из указанной таблицы выписываем формулы для определения функции положения толкателя кулачкового механизма и передаточных кинематических функций 1-го и 2-го порядков. Для удобств пользования этими формулами, их преобразуем к следующему виду:

а) на фазе удаления:

при ,

при ,

при ,

где:

,

б) на фазе возвращения:

при ,

при ,

при ,

где:

,

,

а , либо- относительное значение текущего угла, отсчитываемое от начала фазы удаления, либо возвращения. Поскольку в нашем случае и уголи уголразбиты на 6 равных частей каждый, то относительные их значения составляют:

Т.о. указанные функции в пределах каждой из фаз будут определены в 8-ми равноотстоящих точках.

Расчёты могут быть произведены с помощью программируемого микрокалькулятора типа МК-52. Программа 3, помещённая в «приложении 1», позволяет осуществлять расчет лишь для принятых здесь законов движения. Результаты расчётов выполненных по этой программе, занесены в табл. 2.5.

Задачу определения основных размеров кулачкового механизма – минимального радиуса профиля кулачка , межосевое расстояния(рис 2.7) и угла коромысла О₁О₂ со стойкой ОО₂ при нижнем выстое коромысла - решаем графически. Для этого:

1. На чертеже (приложение 3) выбираем произвольно центр О₂ и в этом центре размещаем вершину угла , который строим при помощи транспортира относительно произвольно направленной его биссектрисы.

2. Проводим стягивающую этот угол дугу радиусом, равным длине коромысла в выбранном масштабе (например,).

3. Построенный угол делим лучами на 6 частей в соответствии со значениямив табл. 2.5 для фазы удаления (коромысло О₁О₂ движется в одном направлении) и на 6 частей для фазы возвращения (коромысло О₁О₂ движется противоположно).

4. На построенных лучах от их пересечения с дугой (п.2) откладываем отрезки в масштабе коромысла () в направлении вектора скоростиконца коромысла, повернутого на 90^° по угловой скорости кулачка ().

При силовом замыкании (пружиной и др.) высшей кинематической пары «кулачек - толкатель» отрезки откладываем лишь для фазы удаления.

Соединяем концы отрезков и строим кривую.

5. Проводим хорду к дуге, описанной центром ролика коромысла (к дуге 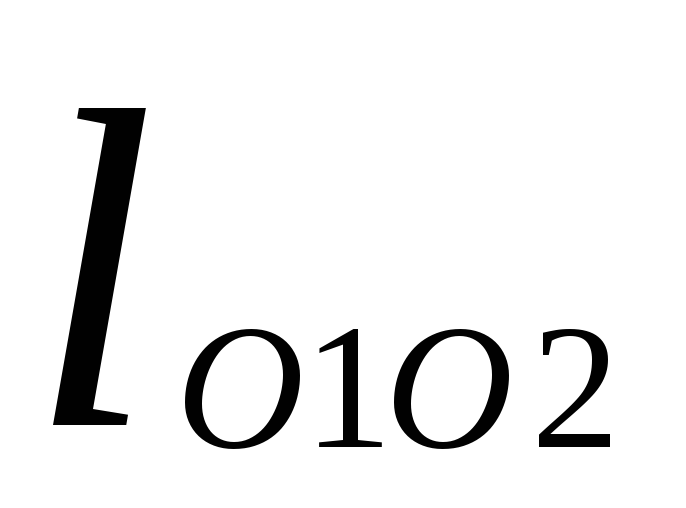). К проведённой хорде под углом давления(при вращательном движении толкателя) проводим касательные к кривой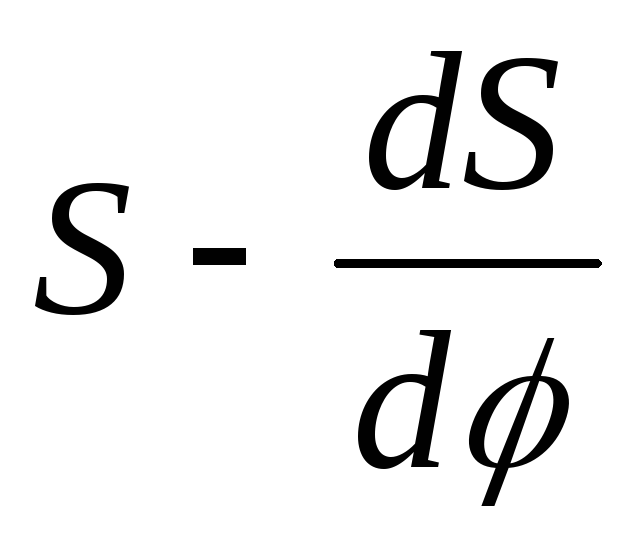на фазе удаления и на фазе возвращения (при силовом замыкании высшей кинематической пары«ролик – кулачёк», эта кривая совпадает с дугой радиуса). Внутри угла, образуемого касательными в наиболее удалённой области их пересечения (приложение 3), выбираем центр О вращения кулачка.

6. Таблица 2.5

	Фаза удаления Закон синусоидальный				Фаза возвращения Закон падающего ускорения			Таблица 2.5.
0	0	0	0	0	25	0	1.19
	0.72	0.147	0.0176		23.15	0.245	0.79
	4.88	0.441	0.053		18.51	0.392	0.397
	12.5	0.588	0.071		12.5	0.44	0
	20.1	0.441	0.053		6.48	0.329	0.397
	24.8	0.147	0.0176		1.85	0.245	0.79
	25	0	0		0	0	1.19

7. Определяем минимальный радиус теоретического профиля кулачка:

м,

межосевое расстояние

м,

транспортиром замеряем минимальный угол коромысла О₁О₂ со стойкой ОО₂ ().

8. Строим кулачек по методу обращения движения.

9. Выбираем радиус ролика как минимум из соотношений:

м,

м.

где (м)- минимальный радиус кривизны теоретического профиля кулачка.

Принимаем мм.

10. Строим рабочий профиль кулачка как эквидистанту к теоретическому профилю, отстоящую на мм от полученного в п.7 теоретического профиля кулачка.

Полученную схему кулачкового механизма совмещаем со схемой несущего механизма. Для этого (чертеж 1, приложения 3):

1. Из центра О вращения кривошипа АО проводим дугу радиусом, равным (в масштабе) межосевому расстоянию в кулачковом механизме. На этой дуге в удобном месте выбираем положение центра О₂ вращения коромысла.

2. Соединяем центры О и О₂. От полученного отрезка ОО₂ откладываем минимальный угол коромысла О₂О₁ со стойкой ОО₂ (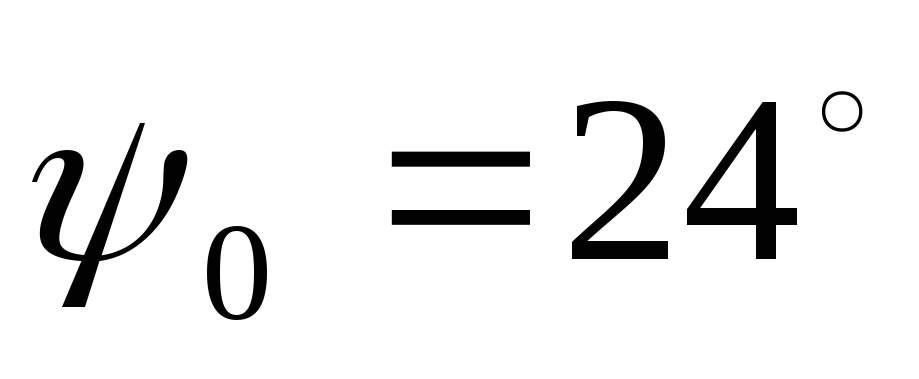). На полученной второй стороне угла от его вершины О₂ откладываем отрезок О₂О₁, изображающий в масштабе длину коромысла кулачкового механизма.

3. Из конца О₁ этого отрезка проводим окружность, в масштабе, изображающую ролик; касательно к этой окружности из центра О вращения кулачка (и кривошипа ОА) проводим окружность (мм.), которая изображает основную шайбу практического профиля кулачка.

Изображенный на чертеже несущего механизма кулачковый механизм находиться в начале фазы удаления и соответствует 9-му положению кривошипа ОА. Транспортиром замеряем угол установки кулачка относительно кривошипа ОА (, где- радиус – вектор профиля кулачка, соответствующий началу фазы удаления в кулачковом механизме).