2.1.2. Синтез зубчатых механизмов.

С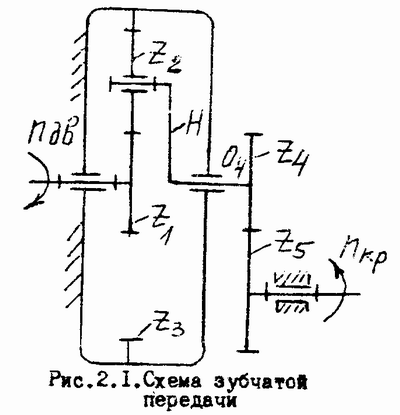хема зубчатой передачи представлена на рис. 2.1. Основу передачи составляет планетарный механизм с передаточным отношением:

Открытая зубчатая передача z₄ – z₅ имеет передаточное отношение:

Синтез (подбор чисел зубьев) планетарной ступени производим на основе следующих четырёх условий (/8/ стр. 420-425).

. Условия выполнения требуемого передаточного отношения:

,

где передаточное отношение от 1-го колеса к водилу H при закрепленном колесе 3 , а передаточное отношение обращенного механизма

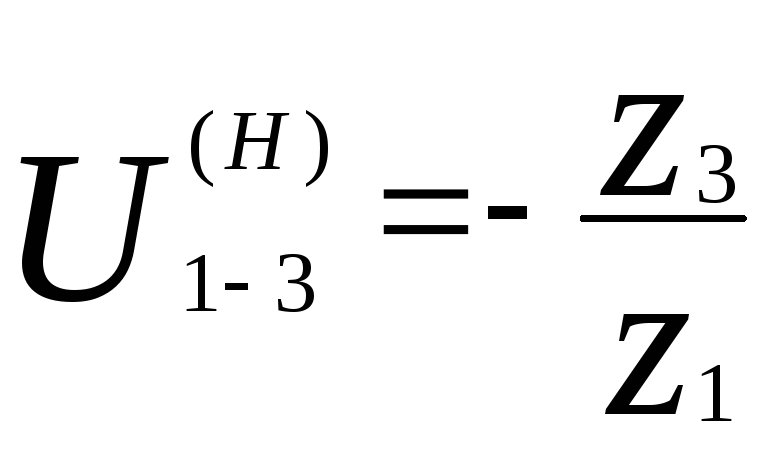
На основания этого из (2.1) получаем:

z₃ = 6.4·z₁

2. Условие правильности зацепления, по которому:

Принимая z₁ = 20, получаем: z₃ = 6.4·z₁ = 6.4·20 = 128 зубьев

3. Условия соосности: z₁ + 2z₂ = z₃,

По условию правильности зацепления: z₃ – z₂ = 128-54 = 74 >8

4. Условия соседства:

из которого число сателлитов:

Т.е. число сателлитов может быть К=1, К=2, либо К=3. С целью обеспечения уравновешенности механизма и более равномерной передачи сил принимаем К=3.

Уточняем передаточное отношение:

Проверяем возможность сборки полученного механизма:

После подстановки чисел:

Это соотношение не удовлетворяется ни при каких целых П и Ц. Поэтому, не меняя величины К (К=3), изменим z₁ и подберем новые значения z₂ и z₃.

Приняв z₁ = 18 зубьев будем иметь:

z₃ = 6.4·18 = 114.2

Принимаем z₃ = 114.

из условия соосности:

z₂ = 0.5·(114-18) = 48 зубьев

и условие соседства: - будет удовлетворяться

Уточнённое значение :

отличается от принятого первоначально

на , что допускается.

Условие сборки

удовлетворяется при любом П, в т.ч. и при П = 0, что соответствует минимальным затратам времени на сборку редуктора (/7/стр. 428).

Окончательно принимаем для планетарного механизма

z₁ = 18, z₂ = 48, z₃ = 114, K = 3

Для уравнительной зубчатой передачи находим уточненное значение передаточного отношения:

Приняв z₄ = z_min = 17, найдём z₅ = z₄·U_4-5 = =4,47·1.94=76,76;

При z₄ = 18 получим z₅ = 81,28, а при z₄ = 16, найдём z₅ = 72,25 и т.д.

Последний вариант обеспечивает наилучшее приближение к требуемому передаточному отношению, хотя и требует незначительного исправления (корригирования) зубьев.

Окончательно принимаем z₄ = 16, z₅ = 72.

Модуль зубчатых колес планетарного редуктора найдём по максимальному моменту в зубчатом механизме, который имеет место на выходном его валу (на валу-водила) Н. Момент на этом валу

,

где номинальная скорость вращения вала двигателя:

Модуль (/1/ стр. 205)

.

Ближайший больший модуль первого ряда по СТ СЭВ 310-76 (/5/ стр. 110), т= 2 мм.

Модуль зубчатых колес открытой передачи рассчитываем по моменту на валу кривошипа: М_кр = М_Н ·U_4-5 = 32,9·4,5 =148,05 Н·м.

Тогда

.

Учитывая повышенный износ при работе без смазки, принимаем для открытой уравнительной передачи m₁ = 5 мм.

Определяем делительные диаметры колёс:

d₁ = m₁z₁ = 2·18 = 36 мм

d₂ = m₁z₂ = 2·48 = 96 мм

d₃ = m₁z₃ = 2·114 = 228 мм

d₄ = m₁z₄ = 5·16 = 80 мм

d₅ = m₁z₅ = 5·72 = 360 мм,

а диаметр водила Н с учётом монтажа в нём сателлитов:

.

Принимаем d_H = 150 мм.