5. Расчет тихоходного вала редуктора

Валы подразделяются на входные (быстроходные), выходные (тихоходные) и промежуточные. Большинство входных валов редукторов выполняют за одно целое с зубчатыми венцами (вал-шестерни) и червяками. Входные и выходные валы имеют выступающий из корпуса редуктора консольный участок, предназначенный для сопряжения с полумуфтой, шкивом, звездочкой и пр.

На валы от зубчатых и червячных колес, червяков, подшипников и других посаженных на них деталей передаются окружные, радиальные и осевые силы, создающие в поперечных сечениях продольные и поперечные силы, изгибающие и вращающие моменты. Таким образом, валы испытывают сложную деформацию – изгиба (растяжения-сжатия) и кручения. Продольные силы создают в сечениях вала нормальные напряжения растяжения или сжатия небольшой величины, поэтому они в расчетах не учитываются.

Действующие на вал силы распределены по длине ступицы, ширине подшипника. При проектном расчете считают эти силы сосредоточенными и приложенными на середине ширины зубчатого венца или подшипника. Эти сечения принимают за расчетные. По длине вала место приложения нагрузки зависит от расположения зубчатых колес, шкивов, муфт, звездочек и опор.

Исходные данные:

Силы, действующие на вал от косозубой цилиндрической передачи (определены при расчете передачи):

– окружная сила (действует в вертикальной плоскости);

– радиальная сила (действует в горизонтальной плоскости);

– осевая сила (действует в горизонтальной плоскости);

– вращающий момент на валу;

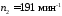– частота вращения вала;

– диаметр делительной окружности зубчатого колеса, установленного на валу;

режим нагружения – постоянный;

– требуемый ресурс;

– диаметр вала под подшипники;

– диаметр вала под колесо;

Расстояние между опорами вала, координаты точек приложения сил определяются по эскизной компоновке редуктора: ;;.

Выходной вал редуктора соединен с приводным валом исполнительного механизма упругой муфтой.

Последовательность расчета

1) Определяем радиальную силу от муфты, действующую на консольный участок вала по формуле:

Принимаем действие этой силы в вертикальной плоскости (как и силы ), направленной на увеличение деформации вала от силы.

2) Используя эскизную компоновку редуктора, составляем расчетную схему вала (рис. 7).

3) Определяем опорные реакции в горизонтальной плоскости XOZ(рис.7б).

Откуда

.

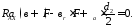
Откуда

.

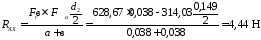Проверка правильности определения реакций:

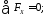
4) Определяем опорные реакции в вертикальной плоскости YOZ(рис. 7в).

Откуда

.

Откуда

.

Проверка правильности определения реакций:

5) Определяем опорные реакции от силы 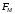(рис. 7г).

Откуда

.

.

Откуда

.

Проверка: .

6) Суммарные реакции в опорах (приведенные в одну плоскость), которые будут использованы в качестве радиальных нагрузок при выборе подшипников качения:

Тогда,

;

.

7) Определяем изгибающие моменты в горизонтальной плоскости XOZ

(рис. 7б).

.

Тогда,

.

Тогда,

Определяем изгибающие моменты в вертикальной плоскости YOZ

(рис. 7в).

.

Тогда,

Определяем изгибающие моменты от силы (рис. 7г).

.

Тогда,

Определяем изгибающий момент в сечении С (под колесом).

Тогда,

8) Суммарный изгибающий момент в сечении под колесом (сечение С – наиболее нагруженное).

Рисунок 7 – Расчетная схема вала.

9) Принимаем: материал вала – сталь 45 и из табл. 4.1 [1,c.83] выписываем его механические характеристики:

Механическая обработка вала – тонкая обточка; вал не подвергается поверхностному упрочнению.

10) Расчёт на сопротивление усталости.

Для опасного сечения вала (сечение С) расчетный коэффициент запаса прочности определяем по формуле:

,

где – коэффициент запаса по напряжениям изгиба,

;

– коэффициент запаса по напряжениям кручения,

,

где – пределы выносливости гладких образцов при симметричном цикле изгиба и кручения;

– коэффициент долговечности, учитывающий режим нагружения и срок службы,

,

т. к. 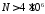, то;

– суммарные коэффициенты, учитывающие влияние всех факторов на сопротивление усталости соответственно при изгибе и кручении;

где – эффективные коэффициенты концентрации напряжений при изгибе и кручении соответственно, определяем по табл. 4.3 [1, с.96] в зависимости от вида концентраторов напряжений: для ступенчатого перехода с галтелью

( ,,):

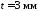при

;

;

для шпоночной канавки, выполненной пальцевой фрезой:

Следовательно, большее влияние оказывает концентратор напряжения переход с галтелью ; поэтому для расчета принимаем

– коэффициент влияния абсолютных размеров поперечного сечения вала определяем по табл. 4.5 [1, с.98], принимаем;

– коэффициент влияния шероховатости поверхности определяем по табл. 4.6 [1, с.98], принимаем;

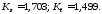
– коэффициент влияния упрочнения, вводимый для валов с поверхностным упрочнением, т.к. вал не подвергается поверхностному упрочнению.

Таким образом,

.

По формулам [1, c.94, ф. 4.14] определяем переменные (амплитудные) составляющие цикл изменения напряжений при изгибе и кручении соответственно:

где – осевой и полярный моменты сопротивления и определяем по формулам [1,c.94, ф. 4.15]

;

.

Тогда,

Коэффициент запаса прочности:

.

Следовательно, вал удовлетворяет условию прочности на сопротивление усталости.