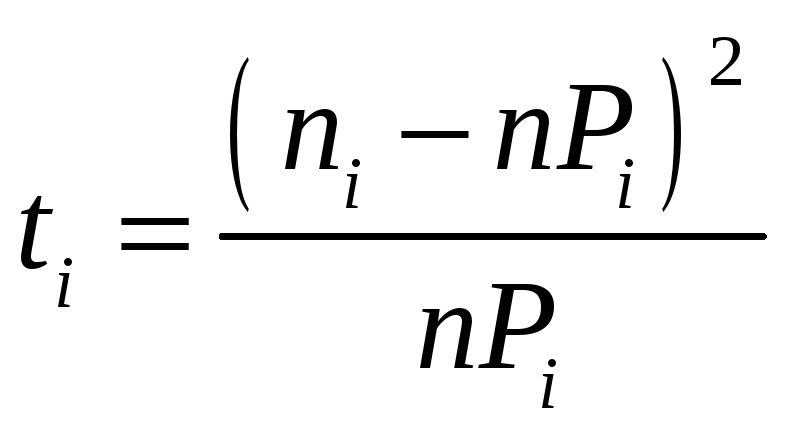математика / Образцы решения заданий 7 и 8 по матем стат

9

Образец оформления задания 7.

В результате некоторого эксперимента были получены данные, записанные в виде статистического ряда.

11,2	12,6	10,9	10,9	15,1	14,1	11,5	15,6	16,1	13,2
16,9	14,9	16,3	14,4	14,7	13	13,1	11,6	15,9	17,9
18,1	11,1	15,1	7,8	16,4	16,5	11,3	17,1	15,9	13,2
12,7	17,6	12,4	18,3	13	16,3	11,3	15,7	19	16,3
18,2	12,1	14,8	11,5	13,2	20,3	11,7	18,7	11,7	18,7

Произвести статистическую обработку результатов измерений:

1) построить интервальный вариационный ряд;

2) построить гистограмму относительных частот, эмпирическую функцию распределения и ее график (кумулянту);

3) найти выборочные числовые характеристики ;

4) по геометрическим характеристикам и по соотношениям между числовыми характеристиками выдвинуть гипотезу о законе распределения признака X;

5) проверить гипотезу о законе распределения признака X по критерию -квадрат при уровне значимости 0,05;

6) найти 95%-ые доверительные интервалы для математического ожидания и среднего квадратического отклонения.

Решение.

1) Сначала составляем дискретный вариационный ряд, записав варианты в порядке возрастания.

7,8	10,9	10,9	11,1	11,2	11,3	11,3	11,5	11,5	11,6
11,7	11,7	12,1	12,4	12,6	12,7	13	13	13,1	13,2
13,2	13,2	14,1	14,4	14,7	14,8	14,9	15,1	15,1	15,6
15,7	15,9	15,9	16,1	16,3	16,3	16,3	16,4	16,5	16,9
17,1	17,6	17,9	18,1	18,2	18,3	18,7	18,7	19	20,3

Для построения интервального вариационного ряда определяем число интервалов по формуле .

. Значит, . Находим длину интервала:

.

- формула, по которой определяются границы интервалов.

Составляем расчетную таблицу в виде интервального вариационного ряда.

№ ин-тер-вала	xi; xi+1)	ci	ni	wi			cini
1	7,8; 9,88)	8,84	1	0,02	0,0096		8,84	78,146
2	9,88; 11,96)	10,92	11	0,22	0,1058		120,12	1311,170
3	11,96; 14,04)	13	10	0,2	0,0962		130	1690
4	14,04; 16,12)	15,08	12	0,24	0,1154		180,96	2728,877
5	16,12; 18,2)	17,16	11	0,22	0,1058		188,76	3239,122
6	18,2; 20,3	19,25	5	0,1	0,0481		96,25	1852,81
Сумма			50	1		S1=724,93		S2=10900,125

- середина интервала; - значения частот;

- относительная частота.

2) Строим гистограмму относительных частот.

Эмпирическая функция распределения выборки находится по формуле:

,

где - число вариант, меньших x.

Строим эмпирическую функцию распределения.

Строим график эмпирической функции распределения (кумулянту).

3) Определяем выборочную среднюю по формуле .

Находим выборочную дисперсию по формуле .

.

Находим среднее квадратическое отклонение .

Для определения моды , сначала выбираем модальный интервал с наибольшей частотой.

В нашем случае это 4-й интервал.

Моду находим по следующей формуле:

, где - начальная граница модального интервала;

- частота модального интервала;

- частота предмодального интервала;

- частота послемодального интервала;

 - длина интервала.

.

Для определения медианы находим медианный интервал. Проверяем по порядку следующие условия:

В нашем случае 4-й интервал является медианным.

Медиану находим по формуле:

, где - начальная граница медианного интервала;

- частота медианного интервала;

- объем выборки;

- сумма частот до медианного интервала;

 - длина интервала.

.

4) Так как гистограмма имеет максимум в середине таблицы с убыванием в стороны, то выдвигаем гипотезу H₀.

H₀: исследуемый признак X распределен по нормальному закону.

Конкурирующая гипотеза H₁: исследуемый признак X распределен по закону, который не является нормальным законом.

В процессе обработки результатов получили, что .

Оцениваем параметры выбранного закона распределения.

Математическое ожидание .

Находим исправленное среднее квадратическое отклонение:

5) Для проверки гипотезы о законе распределения признака X по критерию ²-квадрат при уровне ошибки =0,05 необходимо найти теоретические вероятности P_i попадания случайной величины X в интервал _i по формуле

, где (x)-функция Лапласа.

Для удобства вычислений составим таблицу.

i	xi			i	ni	Pi	nPi
1	7,8	-5	-0,5	(7,8; 9,88)	1	0,0505	2,525
2	9,88	-1,64	-0,4495	(9,88; 11,96)	11	0,1336	6,68
3	11,96	-0,90	-0,3159	(11,96; 14,04)	10	0,2523	12,615
4	14,04	-0,16	-0,0636	(14,04; 16,12)	12	0,2826	14,13
5	16,12	0,58	0,2190	(16,12; 18,2)	11	0,1859	9,295
6	18,2	1,31	0,4049	(18,2; 20,3)	5	0,0951	4,755
7	20,3	5	0,5				

nP_i – теоретические частоты.

Мы видим, что в первой и шестой строках теоретические частоты nP₁<5 и nP₆<5. Значит, первую строку объединяем со второй, а шестую с пятой строкой. В результате получим новую таблицу.

i	nPi	ni
1	9,205	12	0,8487
2	12,615	10	0,5421
3	14,13	12	0,3211
4	14,05	16	0,2706
			=1,9825

Итак, t=1,9825.

Степени свободы определяем по формуле:

k=m-r-1, где m – число интервалов

r – число параметров теоретического распределения.

В нашем случае: k=4-2-1=1.

По таблице значений - критерия Пирсона при k=1 и =0,05 определяем ²_кр=3,8.

Так как t=1,9825<²_кр, то нет оснований отвергнуть гипотезу H₀.

6) Доверительный интервал для математического ожидания при неизвестном среднем квадратическом отклонении нормально распределенной случайной величины X определяется по следующей формуле:

,

где - выборочное среднее;

- исправленное среднее квадратическое отклонение;

n – объем выборки;

t_ - число, которое определяется по таблице значений t_=t(, n) при заданной

надежности  и объеме выборки n

При =0,95 и n=50 определяем t_=2,009.

13,698<a<15,300

Доверительный интервал с заданной надежностью  для среднего квадратического отклонения  нормально распределенного признака X по исправленному среднему квадратическому отклонению определяется по формуле:

при q<1

При =0,95 и n=50 определяем q=0,21.

2,226<<3,410

Образец оформления задания 8.

Экспериментальная зависимость признака Y от фактора X имеет вид:

Xi	2	3	3,5	4	5	6	7	8
Yi	2	1,9	2,1	2,2	2,4	2,3	2,5	2,5

Требуется:

1) найти уравнение линейной регрессии ;

2) найти выборочный коэффициент корреляции ;

3) выяснить значимость уравнения регрессии при ;

4) построить линию регрессии и экспериментальные точки .

Решение.

1) Коэффициенты и b уравнения линейной регрессии находятся по следующим формулам:

;

,

где  число наблюдений. В нашем случае .

Чтобы определить коэффициенты и b, а так же коэффициент корреляции , составляем расчетную таблицу.

Тогда получаем

;

.

Итак, уравнение линейной регрессии имеет вид:

.

2) Выборочный коэффициент корреляции находится по следующей формуле:

.

Тогда получаем

.

3) Выше получили, что коэффициент корреляции .

Так как рассмотренная выборка отобрана случайна, то еще нельзя заключить, что коэффициент корреляции генеральной совокупности также отличен от нуля.

При заданном уровне значимости проверим нулевую гипотезу H₀.

H₀: равенство нулю генерального коэффициента корреляции, т.е. .

Конкурирующая гипотеза H₁: .

Если нулевая гипотеза будет отвергнута, то это значит, что выборочный коэффициент корреляции значимо отличается от нуля, а X и Y коррелированны, т.е. связаны линейной зависимостью. Если нулевая гипотеза будет принята, то выборочный коэффициент корреляции незначим, а X и Y некоррелированы, т.е. не связаны линейной зависимостью.

Для проверки нулевой гипотезы найдем статистику по следующей формуле:

,

где  сумма квадратов, обусловленная регрессией;

 остаточная сумма квадратов;

n – число наблюдений;

l – число групп в корреляционной таблице или число оцениваемых параметров в несгруппированной выборке.

Для определения статистики t составляем расчетную таблицу.

Значения находим из уравнения регрессии, подставляя соответствующие значения . Среднюю выборочную находим следующим образом:

.

Итак, получаем .

В нашем случае число наблюдений . Поскольку рассматривается линейная регрессия, то  число оцениваемых параметров.

При по таблицам распределения Фишера находим .

Вычисляем статистику.

.

Так как , то уравнение линейной регрессии значимо. Принимаем конкурирующую гипотезу H₁: .

4) Строим линию регрессии и экспериментальные точки .