Свойства дифференциальной функции нсв

Свойство 1.Дифференциальная функция неотрицательна, т.е.

.

Свойство 2.Несобственный интеграл от дифференциальной функции в пределах отдоравен единице:

. (2.4)

Теорема 2.1.Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу, равна определенному интегралу от дифференциальной функции, взятому в пределах отдо:

. (2.5)

Следствие 2.3.Еслиплотность распределения вероятностей, то интегральную функцию распределения можно найти по формуле

. (2.6)

График функции называюткривой плотности распределения случайной величиныили просто кривой вероятностей. Отметим особенности, которые присущи любой кривой вероятности:

1) она всегда лежит в верхней координатной полуплоскости;

2) площадь, заключенная между этой кривой и осью абсцисс, равна 1.

Вероятность того, что случайная величина примет значение, заключенное междуи– это площадь заштрихованной криволинейной трапеции.

Пример 2.1.Дана функция распределенияСВX:

.

Найти плотность распределения . Построить графики функцийи. Найти вероятность попадания СВXна отрезок.

Решение.1) Чтобы найти плотность вероятности, воспользуемся формулой 2.3. Тогда получаем

.

2) Строим графики функций и

3) Находим вероятность попадания СВ Xна отрезок, используя формулу 2.2. (Отметим то, что для нахождения вероятности попадания СВXна отрезокможно воспользоваться формулой 2.5).

.



Пример 2.2.Найти интегральную функцию по данной дифференциальной функции

.

Решение.Чтобы найти интегральную функцию распределения, воспользуемся формулой 2.6.

Если , то.

Если , то

.

Если , то

.

Следовательно, получаем следующую интегральную функцию распределения

.



2. Числовые характеристики нсв

Рассмотрим числовые характеристики для непрерывной случайной величины.

Начнем с математического ожидания.

Пусть непрерывная случайная величина задана дифференциальной функцией. Допустим, что все возможные значенияпринадлежат отрезку. Разобьем этот отрезок наnчастичных отрезков длиноюи выберем в каждом из них произвольную точку. Имея в виду задачу:определить математическое ожидание непрерывной величины по аналогии с дискретной, составим сумму произведений возможных значенийx_iна вероятности попадания их в интервал(напомним, что произведениеприближенно равно вероятности попаданияв интервал):

.

Перейдем к пределу при стремлении к нулю длины наибольшего из частичных отрезков, т.е. . Так как– непрерывная функция, тосуществует и равен.

Определение 2.4.Математическим ожиданием непрерывной случайной величины, возможные значения которой принадлежат отрезку, называют определенный интеграл:

. (2.7)

Если возможные значения принадлежат всей числовой оси Ox, то

. (2.8)

По аналогии с дисперсией дискретной величины определяется дисперсия непрерывной величины.

Определение 2.5.Дисперсиейнепрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

. (2.9)

Но для вычисления дисперсии лучше использовать следующую формулу:

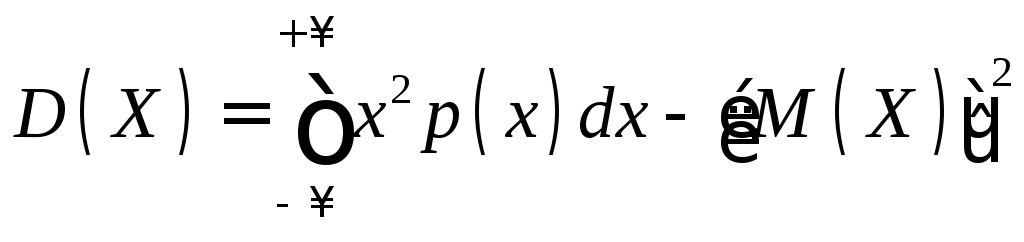. (2.10)

Определение 2.6.Средним квадратическим отклонениемнепрерывной СВXназывают квадратный корень из дисперсии:

. (2.11)

Кстати, можно доказать, что свойства математического ожидания и дисперсии дискретных величин сохраняются и для непрерывных величин.

Определение 2.7.Модойнепрерывной случайной величины называют такое ее значениеM_o, при котором плотность распределения вероятности достигает максимум.

Определение 2.8.Медианойнепрерывной случайной величины называют такое ее значениеM_е, относительно которого равновероятно получение большего или меньшего значения случайной величиныX, т.е.

.

Геометрический смысл M_е:M_е– это абсцисса точки, в которой площадь фигуры, ограниченной кривой, делится пополам.

Пример 2.3.Дана функция распределенияСВX:

.

Найти числовые характеристики СВ X:

Решение.В примере 2.1. для данной интегральной функции распределения была найдена дифференциальная функция распределения. Запишем ее:

.

Далее последовательно вычисляем:

1) .

2) ,

.

3) .

4) Согласно определению 2.7. находим производную функции плотности распределения вероятности.

,

.

В точке функциядостигает максимума, значит,.

5) Найдем медиану НСВ X, используя формулу

.

.

.

Итак, .



Пример 2.4.Случайная величина принимает значения только на сегментес плотностью. Найти коэффициентCи числовые характеристики СВX. Найти вероятность того, что случайная величинаXпопадет в промежуток.

Решение.Так какp(x)=0 при, то из условияследует, что

,

,

Значит, C=1.

Найдем числовые характеристики: математическое ожидание, дисперсию, среднее квадратическое отклонение, моду и медиану.

1) По формуле математического ожидания получаем

.

2) По формуле дисперсии имеем

.

3) .

4) Найдем моду случайной величины. Для этого сначала продифференцируем функцию плотности вероятности.

,

.

В точке функциядостигает максимума, значит,.

5) Найдем медиану случайной величины, используя формулу

.

.

.

6) Найдем вероятность того, что случайная величина Xпопадет в промежуток:

.

